Линейная алгебра и геометрия.
Определители и их свойства.
Определителем квадратной матрицы А=(
) наз. число и обозначается |А| и сопоставляется матрице А по определенному правилу.
1)опред. первого порядка(n=1),т. е. опр. Матрицы А=(a), наз. само число a, которое стоит в этой матрице |А|=a.
2)опред. второго порядка (n=2), т. е. опред. матрицы А= 
, наз. число |А|= 
= 
равное разности произведений элементов главной и побочной диагоналей.
3)опред. третьего порядка(n=3),т.е. опред. матрицы А=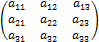 
наз. число, определяемое по формуле |А|= 
.
Правило треугольников(правило Саррюса)
«+» «-»
Свойства определителей: (для любого порядка)
|А|=(
) и в виде набора трех ее строк |А|=˂ 
˃
1)кососиметричность. Если в определителе поменять местами какие-либо две строки, то опред. изменит знак. ˂ ˃= - ˂ ˃.
2)если в определителе какая-то строка, например первая, представляется в виде суммы двух строк: 
, то определитель равен сумме двух опред. ˂ 
˃=˂ 
˃+˂ 
˃
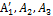3)если какую-то строку опред. умножить на число, то опред. умножится на это число.(общий множитель строки можно вынести за знак определителя)
˂ 
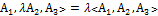
1-3 – основные правила
4)если в опред. две строки равны, то опред. равен нулю.
5)если в опред. какие-то две строки пропорциональны, то опред. равен нулю.
Элементарные преобраз. Первого рода i-ую и j-ую строки меняют местами,
Вторго рода: к i-ой строке прибавляется j-ая, умноженная на число λ
6)при элементарных преобразованиях второго рода опред. не меняется
7)при транспонировании опред. не меняется.
Миноры и алгебраические дополнения. Теорема о разложении опред. по элементам строки или столбца.
Минором 
элемента 
опред. |А| порядка n назыв. опред. порядка n-1, который получается вычеркиванием из А строки и столбца, в которой стоит элемент 
А= ,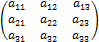 
=| 
|
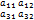Алгебр. Дополнени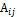е 
= 
, т. е. =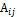 
Для опред. третьего порядка знаки таковы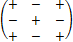 
Теорема. Опред. равен сумме произведений элементов какой-то строки(столбца) на соответствующие алгебраич. дополнения. Например: разложение опред. третьего порядка по первой строке:|А|= 
Док-во
Сгруппируем и вынесем за скобки:|А|= = 
=
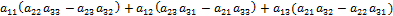системы трех линейных уравнений с тремя неизвестными, правило Крамера.
Системой m линейных уравнений с n неизвестными наз. система вида 
Решением системы наз. набор чисел. Решить систему значит найти все ее решения., если имеется хотя бы 1 решение-совместная, иначе несовместной. если единственное решение-определенная,две системы наз. эквивалентными(если имеют одинаковые решения.)
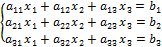
Обозначим через Δ опред. Системы, а через 
, i=1,2,3
Δ=|A|= 
, Δ1= 
, Δ2= 
, Δ3=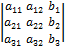 
.
Правило Крамера: теорема. 1)если опред. системы Δ‡0, то система совместна и определена, и ее единственное решение находится (в случае n=3) по формулам Крамера: 
, 
, 
2) если Δ=0, а хотя бы один из 
‡0, то система несовместна.
Если n=2, то теорема:для системы линейных уравнений второго порядка возможны 3 случая: 
