Индексный метод не только характеризует динамику сложного явления, но и анализирует влияние на нее отдельных факторов.
Многие стратегические показатели, характеризующие различные стороны общественных явлений, находятся между собой в определенной связи (часто в виде произведения). Так, объем выработанной продукции связан с уровнем производительности труда и с численностью занятых на предприятии работников; товарооборот является произведением количества проданной продукции на цену; валовой сбор той или иной культуры - произведением урожайности на посевную площадь и т.д. Форма взаимосвязи между такими показателями выявляется на основе теоретического анализа. Статистика характеризует эти взаимосвязи количественно.
Все соотношения в таких произведениях могут рассматриваться как факторы, определяющие значение результативного показателя. Так, объем выработанной продукции на любом предприятии может изменяться за счет совместного изменения двух факторов: производительности труда и численности работающих; товарооборот может изменяться за счет изменения количества (объема) проданных товаров и за счет изменения цен и т.д.
Связь между экономическими показателями находит отражение во взаимосвязи характеризующих их индексов, т.е. если 
, то и 
; а если 
, то и 
.
Поэтому многие экономические показатели тесно связаны между собой и образуют индексные системы.
Система взаимосвязанных индексов дает возможность применять индексный метод для изучения взаимосвязей общественных явлений, проведения факторного анализа с целью определения роли отдельных факторов (не зависимых друг от друга) на изменение сложного явления.
В отечественной статистике принята следующая практика факторного анализа: если результативный показатель можно представить как произведение объемного и качественного факторов, то, определяя влияние объемного фактора на изменение результативного показателя, качественный фактор фиксируют на уровне базисного периода; если же определяется влияние качественного показателя, то объемный фактор фиксируется на уровне отчетного периода.
По существу, любой агрегатный индекс построен по такому принципу обособленного рассмотрения влияния отдельных факторов на изменение сложного показателя.
Рассмотрим построение взаимосвязанных индексов на примере индексов цен, физического объема продукции (если речь идет об отпускных ценах промышленности) или физического объема товарооборота (если речь идет о розничных ценах) и индекса стоимости продукции (товарооборота в фактических ценах).
1. Индексы физического объема и цен являются факторными по отношению к индексу стоимости продукции (товарообороту в фактических ценах):
(8.20)
Таким образом, произведение индекса цен на индекс физического объема продукции дает индекс стоимости продукции (товарооборота в фактических ценах), т.е. образует индексную систему из этих трех индексов.
Если, например, по определенной группе товаров цена единицы товара в отчетном периоде по сравнению с базисным возросла в среднем на 10%, т.е. (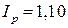
), а физический объем товарооборота (в фиксированных ценах) снизился на 7% (
), то можно определить изменение объема товарооборота в фактических ценах:
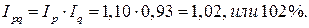
Таким образом, при снижении физического объема товарооборота на 7%, товарооборот в фактических ценах в отчетном периоде по сравнению с базисным вырос на 2% при повышении цен единицу товара в среднем на 10%.
2. Аналогичную взаимосвязь между индексом затрат на производство продукции, индексом себестоимости и индексом физического объема продукции можно записать в виде следующей индексной системы:
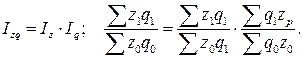(8.21)
3. Индекс изменения общего фонда оплаты труда 
в связи с изменением общей численности работающих 
и заработной платы 
:
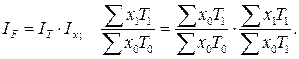(8.22)
4. Индекс изменения объема продукции 
в связи с изменением численности работающих 
и уровня их выработки 
:
(8.23)
5. Индекс изменения объема продукции в связи с изменением объема основных производственных фондов 
и показателя эффективности их использования – фондоотдачи 
:
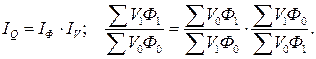(8.24)
6. Индекс изменения валового сбора УП в связи с изменением урожайности 
и посевной площади 
:
(8.25)
К числу взаимосвязанных индексов относятся и индексы переменного состава, постоянного состава и индексы структурных сдвигов. В этой системе динамика среднего показателя (индекса переменного состава) выступает как произведение двух индексов: индекса среднего показателя в неизменной структуре (индекс постоянного состава) и индекса влияния изменения структуры явлений на динамику среднего показателя (индекс структурных сдвигов):
. (8.26)
Индексная система позволяет определить влияние отдельных факторов на формирование уровня результативного показателя, по двум известным значениям индексов найти значение третьего – неизвестное.
Например, если известно, что затраты на производство всей продукции в отчетном периоде по сравнению с базисным выросли на 13% (
) и одновременно уровень себестоимости единицы продукции снизился на 5% (
), то можно определить, что физический объем продукции вырос на 19%:
.
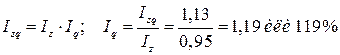Рассмотренные системы представляют собой двухфакторные системы (связь результативного признака с двумя факторами). Но общий признак может зависеть от трех, четырех и более факторов, т.е. связь может быть трехфакторная, четырехфакторная и т.д.
Поэтому общие индексы могут быть разложены также на три и более факторных индекса, объясняющих изменение результативного признака за счет влияния каждого фактора в отдельности.
Применяются два метода расположения общего индекса на частные:
- метод обособленного (изолированного) изучения факторов;
- метод последовательно – цепной (взаимосвязанное изучение факторов).
Поскольку в действительности явления взаимосвязаны, то основной схемой следует считать последовательно - цепной анализ факторов, требующий правильного расположения факторов при построении модели результативного показателя (например, 
).
На первом месте в модели следует ставить качественный фактор. Увеличение цепи факторов на один фактор (например, 
) каждый раз должно приводить к показателю, имеющему реальный экономический смысл.
При определении влияния первого фактора все остальные факторы сохраняются в числителе и знаменателе на уровне отчетного периода.
При построении второго факторного индекса первый фактор сохраняется на уровне базисного периода, третий и все последующие - на уровне отчетного периода.
При построении третьего факторного индекса первый и второй сохраняются на уровне базисного периода, четвертый и все последующие - на уровне отчетного периода и т.д.
Предположим, что . Тогда последовательно - цепное разложение факторов будет иметь вид:
(8.27)
Аналогично строится система взаимосвязанных индексов при четырехфакторной связи и т.д.
Покажем на условном примере проведение факторного анализа сложного показателя с использованием системы взаимосвязанных индексов (задача 8.1).
Задача 8.1. Данные о продаже товаров в розничной торговле района представлены в таблице 8.1.
Таблица 8.1 -Данные о продаже товаров
| Товар | Продано в 1 квартале, млн. руб. | Снижение количества продажи во 2 квартале по сравнению с 1, % |
| Трикотаж | 4,0 | -15 |
| Обувь | 5,2 | -5 |
| Всего | 9,2 | - |
Вычислить:
1. Общий индекс физического объема товарооборота (количества продажи во 2 квартале к 1 кварталу).
2. Среднее изменение цен на товары, если известно, что товарооборот в фактических ценах за это время вырос на 5%.
Решение:
1. Исходя из условия, запишем индивидуальные индексы количеств:
2. Исчислим общий индекс физического объема товарооборота в форме среднего взвешенного арифметического индекса:
Физический объем товарооборота во 2 квартале по сравнению с 1 кварталом уменьшился на 9,4 % или на 860 тыс. руб. (8340 – 9200). Изменение произошло за счет снижения количества продажи (без учета изменения цен).
3. Товарооборот в фактических ценах согласно условию вырос на 5% (следовательно, 
).
4. Используя индексную систему, находим общий индекс цен:
.
Следовательно, цены на данную группу товаров во 2 квартале по сравнению с 1 кварталом увеличились в среднем на 15,9%.
Таким образом, товарооборот в фактических ценах во 2 квартале по сравнению с 1 кварталом вырос на 5% за счет увеличения цен на 15,9% при одновременном снижении количества продажи на 9,4%.
Индексные системы могут применяться и для определения в абсолютном выражении изменения сложного явления за счет влияния отдельных факторов. Расчеты, связанные с определением в абсолютном выражении изменения результативного показателя за счет отдельных факторов, называют разложением абсолютного прироста (сокращения) по факторам .
Так, рассмотренная выше индексная система трехфакторной связи (8.27) может быть представлена в абсолютных величинах следующим образом:
(8.28)
При построении индексов, оценивающих влияние отдельных факторов на изменение сложного явления, необходимо иметь в виду, что общий результат абсолютного изменения этого явления представляет собой сумму абсолютных изменений, обусловленных влиянием исследуемых факторов, формирующих это явление.
Разложения абсолютного прироста по факторам могут быть записаны для самых различных результативных показателей, которые можно представить как произведение объемного фактора на качественный.
Согласно изложенному выше принципу разложение абсолютного прироста (сокращения) по факторам можно записать для рассмотренной выше индексной системы:
(8.29)
(8.30)
,
где 
- абсолютный прирост товарооборота в фактических ценах, т.е. обусловленный изменениями двух факторов – количества проданных товаров и цен;
- абсолютный прирост товарооборота в результате изменения физического объема товарооборота (продажи товара);
- абсолютный прирост товарооборота в результате изменения цен.
Методику факторного анализа рассмотрим на условном примере (задача 8.2).
Задача 8.2. Имеются следующие данные по двум предприятиям (табл.8.2)
Таблица 8.2 - Количество себестоимости произведенной продукции
| Предприятие | Произведено мужской обуви, тыс. пар | Себестоимость единицы продукции, руб. | ||
| Базисный период | Отчетный период | Базисный период | Отчетный период | |
| 
| 
| 
| |
| А | ||||
| Б |
Определить: изменение общих затрат на производство всей продукции под совместным влиянием двух факторов – изменения физического объема продукции и цен каждого из этих факторов в отдельности.
Решение:
1.Для проведения факторного анализа воспользуемся индексной системой:
откуда 
2. Совокупное действие двух факторов на изменение общих затрат определим с помощью индекса затрат на производство продукции (результативного индекса):
.
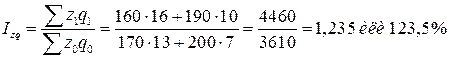Индекс показывает, что затраты на производство всей продукции в отчетном периоде по сравнению с базисным увеличились на 23,5%, что в абсолютном выражении составило:
3. Влияние изменения себестоимости единицы продукции на величину общих затрат определим с помощью факторного индекса себестоимости продукции:
.
Следовательно, за счет изменения себестоимости единицы продукции по каждому предприятию произошло снижение общих затрат на производство продукции на 5,5%, что в абсолютном выражении составило:
4. Влияние изменения объема продукции на величину общих затрат определим с помощью факторного индекса физического объема продукции:
Следовательно, за счет роста общего объема произведенной продукции затраты на производство всей продукции выросли на 30,7%, что в абсолютном выражении составило:
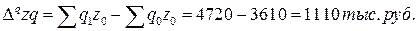
Проверим взаимосвязь индексов в разложение абсолютного прироста по факторам.
