Экономические индексы
8.1 Понятие экономических индексов. Классификация индексов.
8.2 Индивидуальные индексы.
8.3 Сводные индексы.
8.4 Системы индексов.
8.5 Индексы структурных сдвигов.
8.6 Индексы пространственно-территориального сопоставления.
8.7 Система взаимосвязанных индексов. Факторный анализ.
Понятие экономических индексов. Классификация индексов
Индексы являются обобщающими показателями, которые используются в математике, экономике, в метеорологии и других науках.
Экономический индекс - это относительная величина, которая характеризует изменения во времени, в пространстве или по сравнению с некоторым эталоном (план, прогноз, норматив и т.д.).
В статистике различают следующие виды индексов:
1. По степени охвата явления индексы бывают индивидуальные и сводные. Индивидуальные индексы характеризуют изменения отдельных элементов сложного явления. Для изменения динамики сложного явления, составные части которого непосредственно несоизмеримы, рассчитывают сводные (общие) индексы.
Если индексы охватывают некоторую часть элементов сложного явления, то они называются групповыми (субиндексы). Например, индекс цен по группам продовольственных и непродовольственных товаров.
2. По базе сравнения все индексы делят на динамические и территориальные. Первые отражают изменение явления во времени, территориальные же применяются для межрегиональных сравнений.
3. По виду весов индексы бывают с постоянными и переменными весами.
4. В зависимости от формы построения различают индексы агрегатные и средние. Последние делятся на арифметические и гармонические.
5. По характеру объема исследования общие индексыподразделяются на индексы количественных (объемных) и качественных показателей. К первой группе относятся, например, индекс объема продаж долларов США на ММВБ, ко второй – индекс курса доллара США.
6. По объекту исследования различают индексы производительности труда, себестоимости, физического объема продукции, стоимости продукции и т.д.
7. По составу явления можно выделить 2 группы индексов: постоянного (фиксированного) состава и переменного состава.
8. По периоду исчисления индексы делятся на годовые, квартальные, месячные, недельные.
Экономические индексы служат для решения следующих задач:
- измерения динамики социально-экономического явления за два и более периодов времени;
- измерения динамики среднего экономического показателя;
- измерения соотношения показателей по разным регионам;
- определения степени влияния изменения значений одних показателей на динамику других;
- пересчета значения макроэкономических показателей из фактических цен в сопоставимые.
Индивидуальные индексы
Простейшим показателем, используемым в индексном анализе, является индивидуальный индекс, который характеризует изменение во времени (или в пространстве) отдельных элементов той или иной совокупности.
Самыми распространенными индивидуальными индексами являются следующие:
1. Индивидуальный индекс цены:
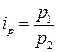, (8.1)
где 
– цена товара соответственно в текущем и базисном периодах.
Этот индекс характеризует изменение цены одного определенного товара в текущем периоде по сравнению с базисным.
2. Индекс физического объема:
, (8.2)
где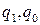 
- объем товара в натуральном выражении соответственно в текущем и базовом периодах.
Он показывает, во сколько раз возрос (уменьшился) выпуск какого-либо одного товара в отчетном периоде по сравнению с базисным, или сколько %-в составляет рост (снижение) выпуска товара.
3. Индивидуальный индекс себестоимости единицы продукции:
, (8.3)
где 
- себестоимость единицы продукции соответственно в текущем и базисном периодах.
4. Индивидуальный индекс товарооборота:
. (8.4)
5. Индивидуальный индекс производительности труда:
;
, (8.5)
где 
- суммарные затраты времени на выпуск данной продукции в чел-час., чел-дн., чел-мес.;
- количество продукции, вырабатываемое в единицу времени (в натуральном выражении);
- затраты рабочего времени на единицу продукции.
. (8.6)
Сводные (общие) индексы
Сводный индекс - это сложный относительный показатель, который характеризует среднее изменение социально-экономического явления, состоящего из непосредственно несоизмеримых элементов. Исходной формой сводного индекса является агрегатная. Особенностью этой формы является то, что в ней непосредственно сравниваются две суммы одноименных показателей.
Здесь индексируемой величиной называется признак, изменение которого изучается (цена товаров, курс акций, затраты рабочего времени на производство продукции и т.д.). Вес индекса – это величина, служащая для целей соизмерения индексируемых величин.
Если строится индекс количественного показателя, то веса берутся за базисный период; при построении индекса качественного показателя используются веса отчетного периода.
Основные виды сводных индексов представлены в таблице 8.1.
Таблица 8.1 - Основные формулы исчисления сводных (общих) индексов
| Наименование индекса | Формула расчета индекса | Что показывает индекс | Что показывает значение индекса, уменьшенное на 100%, т.е. 
| Что показывает разность числителя и знаменателя |
| Индекс физического объема продукции |  
| Во сколько раз изменилась стоимость продукции в результате изменения объема ее производства, или сколько процентов составил рост (снижение) стоимости продукции из-за изменения ее физического объема | На сколько процентов изменилась стоимость продукции в результате изменения объема ее производства | На сколько рублей изменилась стоимость продукции в результате роста (уменьшения) объема ее производства |
| Индекс цен | 
| Во сколько раз изменилась стоимость продукции в результате изменения цен, или сколько процентов составил рост (снижение) стоимости продукции из-за изменения цен | На сколько процентов изменилась стоимость продукции в результате изменения цен | На сколько рублей изменилась стоимость продукции в результате роста (уменьшения) цен |
| Индекс стоимости продукции (товарооборота) | 
| Во сколько раз возросла (уменьшилась) стоимость продукции, или сколько процентов составил рост (снижение) стоимости продукции в текущем периоде по сравнению с базисным | На сколько процентов возросла (уменьшилась) стоимость продукции в текущем периоде по сравнению с базисным | На сколько рублей увеличилась (уменьшилась) стоимость продукции в текущем периоде по сравнению с базисным |
| Индекс физического объема продукции | 
| Во сколько раз изменились издержки производства продукции в результате изменения объема ее производства, или сколько процентов составил рост (снижение) издержек производства продукции из-за изменения физического объема ее производства | На сколько процентов изменились издержки производства продукции в результате изменения объема ее производства | На сколько рублей изменились издержки производства продукции в результате роста (уменьшения) объема ее производства |
| Индекс себестоимости продукции | 
| Во сколько раз изменились издержки производства продукции в результате изменения себестоимости продукции, или сколько процентов составил рост (снижение) издержек производства продукции из-за изменения ее себестоимости | На сколько процентов изменились издержки производства продукции в результате изменения ее себестоимости | На сколько рублей изменились издержки производства в результате роста (уменьшения) себестоимости продукции |
| Индекс издержек производства | 
| Во сколько раз возросли (уменьшились) издержки производства продукции, или сколько процентов составляет рост (снижение) издержек производства продукции в текущем периоде по сравнению с базисным | На сколько процентов возросли (уменьшились) издержки производства продукции в текущем периоде по сравнению с базисным | На сколько рублей увеличились (уменьшились) издержки производства продукции в текущем периоде по сравнению с базисным |
Сводные индексы в средней арифметической и средней гармонической формах
Любой сводный индекс можно представить как среднюю взвешенную из индивидуальных индексов. При этом форму средней нужно выбирать таким образом, чтобы полученный средний индекс был тождествен исходному агрегатному индексу.
Например, мы располагаем данными о стоимости продукции в текущем периоде (
) и индивидуальными индексами цен (
). Тогда в знаменателе сводного индекса цен (
) можно использовать следующую замену:
. (8.7)
Т.о., сводный индекс цен будет выражен в форме средней гармонической из индивидуальных индексов:
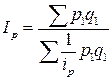. (8.8)
При расчете сводного индекса физического объема товарооборота (
) можно использовать среднюю арифметическую форму. При этом в числителе производится замена: 
.
Тогда индекс примет вид:
. (8.9)
Индекс производительности труда по трудоемкости в средней арифметической форме будет выглядеть следующим образом:
. (8.10)
Система индексов
Индексы могут использоваться для анализа динамики социально-экономических явлений за ряд последовательных периодов. В этом случае для достижения сопоставимости они должны рассчитываться по единой схеме – системе индексов.
В зависимости от информационной базы и целей исследования индексная система может строиться в четырех вариантах.
Рассмотрим систему индексов на примере сводного индекса цен, рассчитываемого за «
» периодов:
1. Цепные индексы цен с переменными весами:
(8.11)
2. Цепные индексы цен с постоянными весами:
(8.12)
3. Базисные индексы цен с переменными весами:
(8.13)
4. Базисные индексы цен с постоянными весами:
(8.14)
