Идеальная гибкая обратная связь

В качестве корректирующего звена выберем идеальное дифференцирующее звено.

.

Пусть охваченное звено имеет:

,

тогда:

. (8.12)

Гибкая обратная связь не влияет на коэффициент передачи охватываемого звена и изменяет коэффициент при р в знаменателе передаточной функции W.

Рассмотрим пример 1:

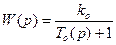
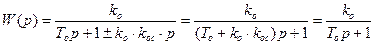
где .

Постоянная времени Т изменилась на k_o×k_oc.

При отрицательной обратной связи Т увеличивается.

При положительной обратной связи Т уменьшается.

Таким образом, гибкая обратная связь изменяет быстродействие без изменения коэффициента передачи звена.

В звене второго порядка гибкая обратная связь сильно уменьшает коэффициент передачи.

Положительная гибкая обратная связь форсирует переходный процесс, как при возрастании, так и при снижении выходного сигнала САР.

 

Рассмотрим пример 2:

Охват дифференцирующей связью с 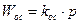интегрирующего звена с .

, (8.13)

где .

Гибкая обратная связь изменяет коэффициент передачи, не меняя типа звена.

 

Гибкая обратная связь по ускорению.

(8.14)

. (8.15)

Такая обратная связь изменяет коэффициент при p². Эта связь применяется для систем 2-го и более высокого порядка.

 

Гибкая инерционная обратная связь.

Реальное дифференцирующее звено:

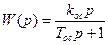. (8.16)

Если такой обратной связью охватить интегрирующее звено, то процесс действия обратной связи можно объяснить так.

Начало переходного процесса. Скорость изменения y(t) велика и в W_ос можно пренебречь, .

В начале переходного процесса гибкая инерционная обратная связь ведет себя как жесткая обратная связь, а охваченное ей интегрирующее звено превращается в апериодическое.

При этом можно повысить быстродействие в начале переходного процесса увеличением коэффициента передачи.

Вторая половина переходного процесса. Постепенно по мере замедления переходного процесса Х_ос спадает до нуля (действует числитель W_ос) и интегрирующее звено начинает вести себя как звено без обратной связи. В статике обеспечивается астатизм системы (ошибка = 0).

 

 

8.5 Охват обратной связью пропорционального звена с большим k_о

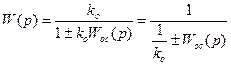, (8.17)

если k >> 1, то

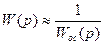. (8.18)

Вывод: если безинерционный усилитель охватить обратной связью, то получим звено с W(p), обратной W_ос(p)

Если 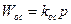, то , т.е. с помощью дифференцирующего звена в обратной связи можно получить интегрирование и наоборот.

Если 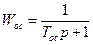, то ;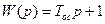

Такой способ получения сложных в реализации передаточных функций нашел широкое применение в АВМ.

Глава 9. Синтез корректирующих устройств