В качестве примера определим передаточные функции для типовых элементов САУ:
1.Генератор постоянного тока (Г). Входной величиной генератора в данном случае является напряжение возбуждения Uтп, выходной - напряжение на его зажимах UГ. Реакция якоря предполагается скомпенсированной, а скорость вращения якоря постоянная. В этом случае ЭДС генератора пропорциональна магнитному потоку, то есть
, (2.29)
В свою очередь поток является функцией тока возбуждения
, (2.30)
Эта зависимость нелинейна и показана на рисунке 2.3.
Рисунок 2.3 Структурная схема генератора постоянного тока
В свою очередь ток возбуждения зависит от напряжения возбуждения согласно следующему уравнению:
, (2.31)
где pВ - число витков обмотки возбуждения;
s - коэффициент рассеяния магнитного потока.
Уравнения (2.29¸2.31) в совокупности определяют искомую зависимость Uг от Uтп. Эта зависимость нелинейна из-за нелинейности характеристики намагничивания генератора (2.30). Линеаризовать такую зависимость по вышеизложенной методике можно, если пренебречь гистерезисом.
Тогда переходя к приращениям переменных, получает следующую систему уравнений
, (2.32)
Здесь 
определяется как тангенс угла наклона касательной к основной кривой намагничивания (рис. 2.3,а).
, (2.33)
где Тв - постоянная времени цепи возбуждения
,
где 
- коэффициент передачи генератора по возбуждению.
Следует заметить, что Тв и kв зависят от выбранной точки установившегося режима, в которой осуществляется линеаризация.
Если перейти к относительным единицам, уравнение (2.33) примет вид:
, (2.34)
где 
При использовании преобразования Лапласа получим следующее выражение для передаточной функции генератора:
, (2.35)
2.Двигатель постоянного тока с независимым возбуждением.
Входными величинами являются напряжение на зажимах якоря UГ (управляющее воздействие) и момент сопротивления на валу Mc(t) (возмущающее воздействие), выходной величиной - скорость вращения вала w.
При составлении уравнений двигателя примем следующие допущения:
1) Реакция якоря отсутствует;
2) Магнитный поток возбуждения электродвигателя постоянен.
С учетом принятых допущений переходные процессы в электродвигателе описываются следующими дифференциальными уравнениями:
, (2.36)
где UГ - ЭДС генератора;
I - ток якорной цепи;
Rэ - полное активное сопротивление якорной цепи системы Г-Д;
М=СмФI - вращающий момент двигателя;
J - момент инерции всех движущихся частей, приведенный к валу двигателя;
Е=СеФw - ЭДС двигателя;
Lэ - индуктивность якорной цепи системы Г-Д.
Так как поток двигателя постоянен, то для момента и ЭДС двигателя можно записать:
; 
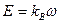, (2.37)
где kе=Се×Ф, kм=См Ф.
Введя эти соотношения в уравнение (2.36), получим
, (2.38)
Производя преобразования Лапласа над уравнениями (2.38), получим:
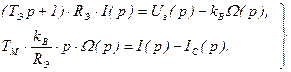, (2.39)
здесь 
- электромагнитная постоянная времени якорной цепи системы Г-Д;
- электромеханическая постоянная системы Г-Д.
Учитывая приведенные выше понятия о передаточной функции и структурной схеме, системе уравнений (2.39) можно поставить в соответствие структурную схему электродвигателя постоянного тока, представленную на рисунке 2.4.
Рисунок 2.4 Структурная схема электродвигателя постоянного тока
Разрешая уравнения (2.39) относительно выходной величины w и управляющего (UГ) и возмущающего (Iс) воздействий, получим:
, (2.40)
Полагая Iс=0, получим передаточную функцию по управляющему воздействию:
, (2.41)
При Uг =0 получим передаточную функцию по возмущающему воздействию
, (2.42)
3.Тиристорный преобразователь.
При анализе тиристорного преобразователя как объекта управления примем, что он является безинерционным звеном и инерционность его определяется фильтром на входе системы импульсного управления. Правомочность такого допущения рассматривается в курсе «Автоматическое управление электроприводами». С учетом принятого допущения передаточная функция тиристорного возбудителя имеет вид
, (2.43)
где ТП - суммарная постоянная времени тиристорного преобразователя;
kП - коэффициент передачи тиристорного преобразователя.
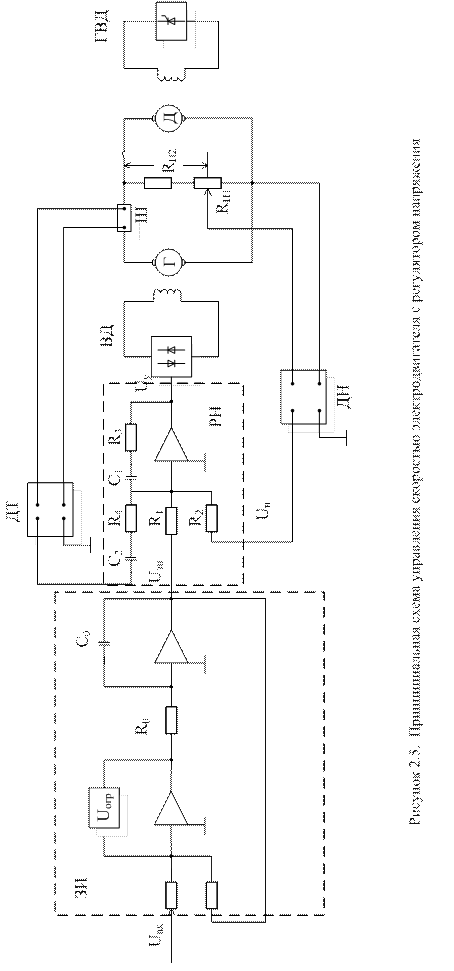
4. Передаточные функции регуляторов и обратных связей (рисунок 2.5).
Для регулятора напряжения (РН) можно записать следующее уравнение:
, (2.44)
где Z0(p), Zзн(p), Zн(p), Zт(p) - комплексные сопротивления, соответственно, в цепи обратной связи РН, задающего напряжения Uзн, обратной связи по напряжению Uн, обратной связи по току Uт.
, (2.45)
, (2.46)
, (2.47)
, (2.48)
Учитывая (2.44) и (2.45¸2.48) для передаточной функции и регулятора напряжения и обратных связей можно записать следующие выражения:
1) для передаточной функции РН
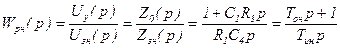, (2.49)
где Тон=С1R3 - постоянная времени в обратной связи регулятора; Тин=С1R1 - постоянная интегрирования регулятора;
2) для передаточной функции обратной связи по напряжению
, (2.50)
где kи=kдн×kп - коэффициент передачи измерителя напряжения;
- коэффициент передачи датчика напряжения ДН-2;
- коэффициент передачи потенциометра;
3) для передаточной функции обратной связи по току
, (2.51)
где T1=R1×C2; T2=C2×R4;
ki=kдт×kш = 
- коэффициент передачи измерителя тока;
kдт - коэффициент передачи датчика тока;
- коэффициент передачи шунта.
Задатчик интенсивности при единичном входном воздействии можно представить передаточной функцией
, (2.52)
Соединяя звенья с передаточными функциями (2.35, 2.39, 2.43, 2.49, 2.50, 2.51, 2.52) в последовательности обусловленной принципиальной схемой, получим структурную схему САУ, представленную на рисунке 2.6
