Основная сложность при выводе уравнений звеньев состоит в установлении степени идеализации и упрощения звеньев. Главным упрощением является получение линейных дифференциальных уравнений звеньев. Это происходит путем линеаризации нелинейных характеристик звеньев.
Математически линеаризация нелинейных характеристик звеньев определяется разложением нелинейной аналитической функции в ряд Тейлора. Принимается, что движение происходит в пределах малых отклонений от установившегося состояния, а производные имеют единственное и конечное значения, отличное от 0. В противном случае уравнение нелинеаризуемо. Представление аналитической функции в виде ряда, содержащего сумму приращений, основано на использовании теоремы Лагранжа о конечном приращении и теоремы Тейлора, являющейся обобщением теоремы Лагранжа.
Для непрерывной функции Y=f(X), имеющей n непрерывных производных в замкнутом интервале a£X£a+DX, формула Тейлора имеет вид
(2.1)
В частном случае, когда а=0, получаем ряд Маклорена:
(2.2)
Если функция зависит от двух переменных, то есть y=f(x,z), то разлагая в ряд, получим
(2.3)
где y0 - значение выходной величины у для рассматриваемого состояния;
х - нелинейный остаток ряда Тейлора, содержащий отклонения Dx и Dz в данной точке во второй и более высокой степени.
При малых отклонениях от точки у0 величиной нелинейного остатка Х можно пренебречь и (2.3) перепишем в виде
(2.4)
Таким образом, линеаризация производится отбрасыванием нелинейного остатка.
В САУ обычно уравнения составляются в отклонениях от данного состояния, то есть
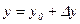(2.5)
Подставляя (2.5) в (2.4), то есть вычитая уравнение статики, получим:
(2.6)
Уравнение (2.6) можно привести к безразмерной форме, относя отклонения Dx, Dz и Dу к их базисным величинам.
Частные производные в уравнениях, например, 
означают, что надо в общем виде взять частные производные от f и х, после чего вместо переменной х подставить ее постоянное значение х=х0. Следовательно, все частные производные уравнения (2.6) представляют собой некоторые постоянные коэффициенты.
Уравнение (2.6) описывает тот же переходный процесс, что и (2.3), но разница между ними следующая:
1)Уравнение (2.6) приближенное, так как отброшены малые высшего порядка (звено идеализировано).
2)Неизвестные не прежние х и z в уравнении (2.3), а отклонения Dx и Dz с постоянными коэффициентами и 
.
Линеаризация нелинейных функций методом малых отклонений графически означает замену кривой отрезками касательной к этой кривой в данной точке А (рисунок 2.1,а). Замена в уравнении (2.4) у=у0+Dу эквивалентна переносу начала координат в точку С (рисунок 2.1, б).
Рисунок 2.1 Линеаризация статического звена
Показанная процедура линеаризации нелинейных звеньев приводит к приближенному описанию их линейными дифференциальными уравнениями в отклонениях (вариациях).
Такая линеаризация применима:
1) Только для малых отклонений Dх около установившегося значения.
2) Так как линеаризация основана на разложении функции в ряд Тейлора, она применима только для непрерывно дифференцируемых нелинейностей.
Такие нелинейности называются линеаризуемыми. Если нелинейность не удовлетворяет этим требованиям, то она называется существенно нелинейной.
В теории автоматического управления принята определенная форма записи уравнений элементов и систем.
При этом уравнение (2.6) должно записываться так:
(2.7)
Здесь 
- оператор дифференцирования по времени;
; 
- приращения переменных в относительных единицах;
- коэффициенты передачи;
; 
- постоянные времени.
Такая форма записи имеет следующие особенности:
1. Выходная величина и ее производные находятся в левой части уравнения, а входная величина и ее производные - в правой.
2. Коэффициент при приращении выходной величины равен единице (в результате деления обеих частей уравнения на 
).
3. Приращения переменных обозначаются строчными буквами и выражены в относительных единицах.
4. Коэффициенты левой части уравнения - постоянные времени. Размерность их - секунда в степени, равной порядку производной, перед которой стоит данный коэффициент.
