Уравнение (2.7) можно рассматривать как сокращенную форму записи дифференциального уравнения, и оно может быть решено классическими методами теории дифференциальных уравнений.
Символический метод, сокращая запись дифференциальных уравнений, не содержит никаких приемов, облегчающих их решение.
Следует заметить, что такой метод алгебраизации дифференциальных уравнений справедлив для случая, когда начальные условия равны нулю.
Второй путь алгебраизации дифференциальных уравнений основывается на преобразовании Лапласа.
Так как преобразование Лапласа изучалось в курсах «Высшей математики» и «Теоретических основах электротехники», вспомним лишь основные выводы операторного метода.
Преобразование Лапласа представляет собой интеграл
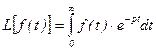, (2.8)
при помощи которого исходная функция f(t), удовлетворяющая условию f(t)=0 при t<0 и еще ряду условий и называемая оригиналом, преобразуется в функцию F(t) комплексного переменного p=s+jw. Функцию F(p) называют изображением оригинала f(t). Символически преобразование Лапласа записывают следующим образом:
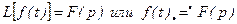. (2.9)
Последнее соотношение читается так: оригиналу f(t) соответствует изображение F(p).
Ценность преобразования Лапласа состоит в том, что с его помощью операции дифференцирования оригинала заменяются умножением на p изображения, а операции интегрирования оригинала заменяются делением на р изображения. Поэтому интегро-дифференциальные уравнения относительно оригиналов заменяются алгебраическими уравнениями относительно изображений. Нахождение оригинала по имеющемуся изображению выполняется при помощи обратного преобразования Лапласа, которое обозначается так:
, (2.10)
где L-1 - символ обратного преобразования.
1.Свойство линейности.
Для любых постоянных А и В
, (2.11)
2.Дифференцирование оригинала.
Если функция f(t) и ее производная f ¢(t) являются оригиналами и F(p) есть изображение оригинала f(t), то справедливо равенство
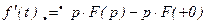(2.12)
И вообще, если n -я производная fn(t) является функцией оригинала, то
(2.13)
3.Дифференцирование изображения по p сводится к умножению на - t оригинала или вообще
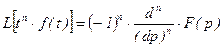, (2.14)
4.Теорема подобия. Для любого a>0
, (2.15)
5.Интегрирование оригинала.
Интегрирование оригинала сводится к делению изображения на р:
, (2.16)
6.Интегрирование изображения. Если 
сходится, то он служит изображением функции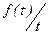 
:
, (2.17)
7.Теорема запаздывания. Для любого положительного t
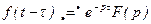, (2.18)
8.Теорема смещения. Для любого комплексного р0
, (2.19)
9.Теорема умножения. Произведение двух изображений F(p) и G(p) так же является изображением, причем
, (2.20)
10.Теорема разложения. Если функция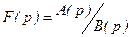 
- правильная рациональная дробь, то оригиналом ее служит функция.
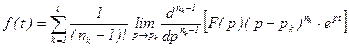, (2.21)
где pk - полюсы F(p) кратности nk и l - число различных корней.
Если все полюсы F(p) простые, то формула (2.21) упрощается и принимает вид
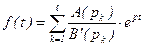, (2.22)
Рассмотрим простой случай, когда на систему (элемент) (рисунок 2.2) действует одно управляющее x(t) и одно возмущающее f(t) воздействие.
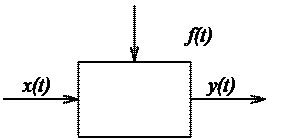
Рисунок 2.2 Простейшее звено САУ
Динамика линейной стационарной системы или элемента может описываться линейным дифференциальным уравнением:
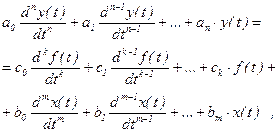(2.23)
где a0, a1,..., an; b0, b1,..., bm; c0, c1,..., ck – коэффициенты дифференциального уравнения; y(t) - выходная величина.
Производя алгебраизацию уравнения, пользуясь свойствами (2.11¸2.21) и считая начальные условия нулевыми, получаем:
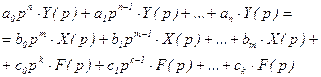(2.24)
или
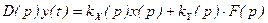, (2.25)
где
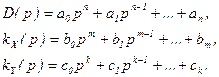
Из уравнения (2.25) следует:
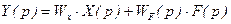, (2.26)
где
,
.
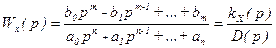Уравнение (2.26) характеризует принцип суперпозиции, на основании которого выходная величина y(t) может быть определена как алгебраическая сумма составляющих, вызванных воздействиями x(p) и f(p).
Если положить f(p) равным нулю, то
; 
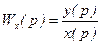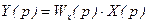, (2.27)
Аналогично, полагая x(p)=0, получим;
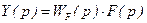, (2.28)
Дробь W(p) называется передаточной функцией звена. Таким образом, понятие «передаточная функция» можно сформулировать таким образом: передаточной функцией звена W(p) называется отношение изображения сигнала на выходе системы (элемента) к изображению входной величины при нулевых начальных условиях.
Передаточная функция является одним из основных понятий в теории автоматического управления.
Если на систему (элемент) действует несколько независимых воздействий, приложенных в различных местах, то она характеризуется несколькими передаточными функциями. Поэтому, говоря о передаточной функции, нужно указать, по отношению к какому воздействию она составлена.
Например, Wx(p) называют передаточной функцией по управляющему воздействию, а Wf(p) - передаточной функцией по возмущающему воздействию.
Сравнивая (2.26), (2.27), (2.28) с (2.7) легко установить, что передаточная функция совпадает с символической формой записи. Разница состоит в том, что в первом случае p обозначает комплексную переменную s+jw, а во втором символ дифференцирования d/dt.
На основании вышеизложенного можно составить следующую последовательность операций при математическом описании САУ:
1) Система расчленяется на отдельные звенья.
2) Определяются переменные величины в звеньях системы, выражающие воздействие одного звена на другое.
3) Составляется уравнение динамики звена.
4) Выявляется характер зависимости переменных величин звена от различных факторов, которые могут быть заданы аналитически или графически.
5) Осуществляется линеаризация полученного нелинейного уравнения, если она возможна.
6) Производится линеаризация уравнений при помощи ряда Тейлора.
7) Для получения линеаризированного уравнения в отклонениях составляется уравнение статики для режима, существовавшего до начала возмущения.
8) Из уравнения динамики вычитается уравнение статики, в результате чего получают уравнение в отклонениях или в вариациях.
9) В левой части уравнения записывают выходную величину и ее производные по времени, а в правой все остальные члены.
10) Уравнения записываются в операторной форме, а коэффициент при выходной величине приводится к единице.
11) По уравнениям динамики отдельных звеньев составляется уравнение регулирования системы в целом.
12) Все звенья системы представляют в виде передаточных функций.
13) По передаточным функциям элементов составляется структурная схема САУ.
В заключении сделаем некоторые обобщения:
Любая САУ, независимо от ее сложности, может быть разложена на отдельные звенья, что является непременным условием при ее математическом описании.
Линеаризация нелинейных уравнений производится путем разложения нелинейной аналитической функции и отбрасыванием нелинейного остатка, содержащего отклонения переменных во второй и более высокой степени. Основанием для такого пренебрежения служит предположение о достаточной малости отклонений всех переменных величин.
Линеаризация нелинейных функций методом малых отклонений графически означает замену кривой отрезком касательной в данной точке и эквивалентна переносу начала координат в эту точку.
Одной из форм алгебраизации дифференциальных уравнений является символическая форма записи. В этом случае оно может быть решено только классическими методами теории дифференциальных уравнений.
Преобразование Лапласа можно рассматривать как одну из форм алгебраизации дифференциальных уравнений. Однако в этом случае операция дифференцирования оригинала заменяется умножением на Р изображения, а операция интегрирования оригинала - делением на Р изображения. Дифференциальное уравнение в этом случае может быть решено при помощи обратного преобразования Лапласа.
Одним из основных понятий в теории автоматического управления является понятие о передаточной функции.
Передаточная функция совпадает с символической записью. При символической форме записи оператор р обозначает символ дифференцирования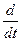 
, а при записи в виде передаточной функции р обозначает комплексную переменную p=s+jw.
Согласно принципу суперпозиции, выходная величина в линейных системах может быть определена как алгебраическая сумма составляющих, вызванных различными воздействиями. В связи с этим, передаточные функции составляются относительно этих воздействий и система имеет число передаточных функций, равное числу воздействий.
