Спектральные характеристики (положения максимумов полос, их полуширина, интенсивность) индивидуальной молекулы зависят от масс составляющих ее атомов, геометрического строения, особенностей межатомных сил, распределения заряда и др. Рассмотрим простейший случай двухатомной молекулы AB.
Молекулу можно представить в виде двух шариков с массами mA и mB, связанных между собой упругой связью с равновесным расстоянием re (рис. 4.1). При смещении шариков A и B из положения равновесия на расстояние Δr возникает возвращающая сила f, стремящаяся вернуть систему в исходное равновесное положение. Сила f описывается с помощью закона Гука:
(4.1)
Δr=r-re – изменение длины связи, k- силовая постоянная связи.
Рис.4.1 Модель двухатомной молекулы AB с равновесным расстоянием re (а) и возникновение возвращающей силы f при изменении расстояния между атомами на Δr
Движение, происходящее после смещения шариков A и B из положения равновесия называется простым гармоническим колебанием. Потенциальная энергия Vгарм системы гармонического осциллятора, состоящего из двух атомов, связанных упругой химической связью, определяется выражением:
(4.2)
Функция V(r) представляет собой симметричную параболу, проходящую через точку минимума, соответствующую равновесному межъядерному расстоянию re (рис.4.2).
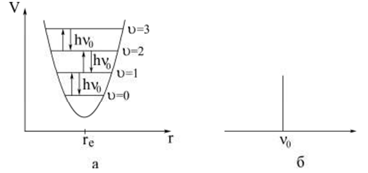
Рис.4.2 Кривая потенциальной энергии и уровни колебательной энергии гармонического осциллятора (а). Схематический колебательный спектр гармонического осциллятора (б).
Колебательная энергия гармонического осциллятора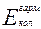 
квантуется по закону:
(4.3)
h - постоянная Планка, n =0, 1, 2, …- колебательное квантовое число, ν0 – частота колебаний гармонического осциллятора, описываемая уравнением:
(4.4)
k – силовая постоянная связи, M=mAmB/(mA+mB) – приведенная масса двухатомной системы AB.
В результате квантования энергии 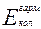гармонический осциллятор характеризуется набором равноотстоящих энергетических уровней, отличающихся друг от друга на одинаковую величину hν0 (рис.4.2). Разрешенными являются только переходы между соседними уровнями, т.е. правило отбора для перехода между колебательными уровнями гармонического осциллятора имеет вид:
Δn=±1 (4.4)
В результате колебательный спектр гармонического осциллятора представляет собой только одну линию с частотой ν0.
В отличие от модели гармонического осциллятора колебания реальных молекул ангармоничны. Потенциальная энергия ангармонического осциллятора Vангарм описывается функцией Морзе:
(4.5)
D – энергия диссоциации связи, ∆r - смещение атомов из положения равновесия, a - постоянная, определяемая выражением:
(4.6)
ν0 – частота осциллятора, M – приведенная масса.
Колебательная энергия ангармонического осциллятора квантуется согласно закону:
(4.7)
По мере увеличения квантового числа n колебательные уровни будут постепенно сближаться (рис.4.3а). В случае ангармонического осциллятора (реальной молекулярной системы) могут реализовываться переходы не только между соседними колебательными уровнями с ∆n =1, но и переходы с ∆n =2, 3, … Это приводит к появлению в колебательном спектре нескольких полос с частотами ν, ν1, ν2. (рис. 4.3б).
Рис. 4.3 Кривая потенциальной энергии и уровни колебательной энергии ангармонического осциллятора (а). Схематический колебательный спектр ангармонического осциллятора (б)
Полоса спектра, отвечающая переходу между колебательными уровнями n =0 →1 (∆n =1) называется основной частотой. Колебательный переход между уровнями с n =0 →2 (ν1) называется первым обертоном, n=0→3 (ν2) вторым обертоном.
