4.1. –ад≥ус-вектор матер≥альноњ точки зм≥нюЇтьс€ з часом за законом 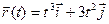 , де
, де  ,
,  Ц орти осей
Ц орти осей  ≥
≥  . ¬изначити дл€ моменту часу
. ¬изначити дл€ моменту часу  : 1) модуль швидкост≥; 2) модуль прискоренн€.
: 1) модуль швидкост≥; 2) модуль прискоренн€.
ƒано:
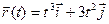

|
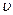 Ц? Ц?
 Ц? Ц?
|
јнал≥з
«а означенн€м миттЇва швидк≥сть визначаЇтьс€ за формулою:
 .
.
ћиттЇве прискоренн€ матер≥альноњ точки визначаЇтьс€:
 .
.
« врахуванн€м, що 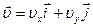 , маЇмо
, маЇмо  ,
, 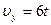 .
.
ќск≥льки  , то
, то 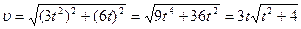 .
.
¬≥дпов≥дно дл€ прискоренн€:  ,
, 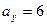 ≥
≥  .
.
ќтже,  .
.
ќбчисленн€:
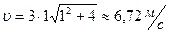 ,
, 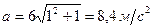 .
.
¬≥дпов≥дь: модуль швидкост≥ дл€ моменту часу  р≥вний
р≥вний  , а модуль прискоренн€
, а модуль прискоренн€  .
.
4.2. олесо автомашини обертаЇтьс€ р≥вноспов≥льнено. «а час  воно зм≥нило частоту в≥д
воно зм≥нило частоту в≥д  до
до  . ¬изначити: 1) кутове прискоренн€ колеса; 2) число повних оберт≥в, зроблених за цей час.
. ¬изначити: 1) кутове прискоренн€ колеса; 2) число повних оберт≥в, зроблених за цей час.
ƒано:


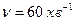
| —I



|
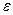 Ц? Ц?
 Ц? Ц?
|
јнал≥з
утова швидк≥сть п≥д час обертального руху зм≥нюЇтьс€ за законом: 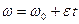 .
.
¬раховуючи, що  , то
, то  . ќстаточно:
. ќстаточно:

≥нематичне р≥вн€нн€ обертального руху:  , де
, де  Ц кутове перем≥щенн€ матер≥альноњ точки. «г≥дно умови задач≥:
Ц кутове перем≥щенн€ матер≥альноњ точки. «г≥дно умови задач≥:  .
.
¬раховуючи, що  , то
, то 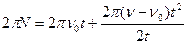 . «в≥дки
. «в≥дки  .
.
ќбчисленн€:
 ,
,  .
.
¬≥дпов≥дь: кутове прискоренн€ колеса  , к≥льк≥сть повних оберт≥в колеса
, к≥льк≥сть повних оберт≥в колеса 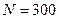 .
.
4.3. ”здовж похилоњ площини, що утворюЇ з горизонтом кут  , п≥дн≥мають т≥ло. оеф≥ц≥Їнт терт€ становить
, п≥дн≥мають т≥ло. оеф≥ц≥Їнт терт€ становить  . ѕ≥д €ким кутом
. ѕ≥д €ким кутом 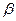 до похилоњ площини потр≥бно спр€мувати силу, щоб вона була найменшою?
до похилоњ площини потр≥бно спр€мувати силу, щоб вона була найменшою?
ƒано:


|
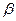 Ц? Ц?
|
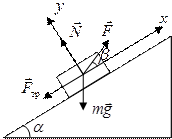 јнал≥з
јнал≥з
ќск≥льки в умов≥ задач≥ не зазначено, що т≥ло рухаЇтьс€ з прискоренн€м, то вважатимемо рух т≥ла р≥вном≥рним (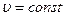 ≥
≥ 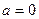 ).
).
«г≥дно з другим законом Ќьютона  .
.
—проектуЇмо сили на координатн≥ в≥с≥  ≥
≥  .
.
 .
.
 .
.
«а означенн€м  ≥, враховуючи, що
≥, враховуючи, що  , маЇмо
, маЇмо
 .
.
« отриманого р≥вн€нн€ виокремимо силу 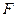 :
:  .
.
—ила 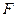 буде м≥н≥мальною, €кщо знаменник матиме максимальне значенн€. «алежн≥сть сили
буде м≥н≥мальною, €кщо знаменник матиме максимальне значенн€. «алежн≥сть сили 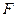 в≥д кута
в≥д кута 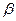 досл≥димо на екстремум. ѕершу пох≥дну в≥д знаменника прир≥вн€Їмо до нул€ ≥ отримаЇмо:
досл≥димо на екстремум. ѕершу пох≥дну в≥д знаменника прир≥вн€Їмо до нул€ ≥ отримаЇмо:
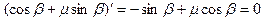 , зв≥дси
, зв≥дси  .
.
ћи знайшли критичну точку функц≥њ  . ƒруга пох≥дна в≥д знаменника при
. ƒруга пох≥дна в≥д знаменника при  менша за нуль. ÷е означаЇ, що точка Ї максимумом. ј отже сила
менша за нуль. ÷е означаЇ, що точка Ї максимумом. ј отже сила 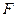 , прикладена до т≥ла, маЇ м≥н≥мальне значенн€.
, прикладена до т≥ла, маЇ м≥н≥мальне значенн€.
¬≥дпов≥дь: сила повинна бути спр€мована п≥д кутом  до похилоњ площини.
до похилоњ площини.
4.4. «найти першу косм≥чну швидк≥сть дл€ «емл≥, тобто м≥н≥мальну швидк≥сть, €ку треба надати т≥лу, щоби вивести його на навколоземну орб≥ту.
ƒано:

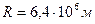
|
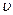 Ц? Ц?
|
јнал≥з
Ќа супутник, що рухаЇтьс€ по колу рад≥уса  , д≥Ї сила т€ж≥нн€ «емл≥, €ка Ї доцентровою силою ≥ надаЇ йому нормального прискоренн€
, д≥Ї сила т€ж≥нн€ «емл≥, €ка Ї доцентровою силою ≥ надаЇ йому нормального прискоренн€  . «а другим законом Ќьютона:
. «а другим законом Ќьютона:  , де
, де  Ц маса супутника,
Ц маса супутника,  Ц маса «емл≥,
Ц маса «емл≥,  Ц рад≥ус «емл≥. «в≥дси
Ц рад≥ус «емл≥. «в≥дси  .
.
якщо висота над «емлею мала пор≥вн€но з рад≥усом «емл≥  , поблизу поверхн≥ «емл≥
, поблизу поверхн≥ «емл≥  .
.
ќбчисленн€:
 .
.
¬≥дпов≥дь: перша косм≥чна швидк≥сть  .
.
4.5. ѕри центральному пружному удар≥ т≥ло масою  стикаЇтьс€ з нерухомим т≥лом масою
стикаЇтьс€ з нерухомим т≥лом масою  , в результат≥ чого швидк≥сть першого т≥ла зменшуЇтьс€ в 2 рази. ¬изначити: 1) у ск≥льки раз≥в маса першого т≥ла б≥льша за масу другого т≥ла; 2) к≥нетичну енерг≥ю
, в результат≥ чого швидк≥сть першого т≥ла зменшуЇтьс€ в 2 рази. ¬изначити: 1) у ск≥льки раз≥в маса першого т≥ла б≥льша за масу другого т≥ла; 2) к≥нетичну енерг≥ю  другого т≥ла п≥сл€ удару, €кщо к≥нетична енерг≥€
другого т≥ла п≥сл€ удару, €кщо к≥нетична енерг≥€ 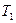 першого т≥ла до удару була р≥вна
першого т≥ла до удару була р≥вна  .
.
|
|
|
ƒано:


|
 Ц? Ц?
 Ц? Ц?
|
јнал≥з
 «апишемо закони збереженн€ ≥мпульсу ≥ енерг≥њ дл€ абсолютно пружного удару двох т≥л. ќск≥льки друге т≥ло до удару перебувало в стан≥ спокою, то
«апишемо закони збереженн€ ≥мпульсу ≥ енерг≥њ дл€ абсолютно пружного удару двох т≥л. ќск≥льки друге т≥ло до удару перебувало в стан≥ спокою, то

¬раховуючи, що  , та
, та  , маЇмо:
, маЇмо:

« верхнього р≥вн€нн€  ; з нижнього:
; з нижнього: 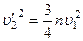 .
.
ќск≥льки  , то
, то  , зв≥дки
, зв≥дки  . ќтже,
. ќтже, 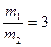 .
.
–≥вн€нн€ (2) запишемо у вигл€д≥:  .
.
¬раховуючи, що  , тод≥
, тод≥  . ќтже,
. ќтже,
 .
.
ќбчисленн€:
 .
.
¬≥дпов≥дь: маса першого т≥ла б≥льша за масу другого т≥ла у  рази, к≥нетична енерг≥€ другого т≥ла п≥сл€ удару р≥вна
рази, к≥нетична енерг≥€ другого т≥ла п≥сл€ удару р≥вна  .
.
4.6. ул€ масою  , що летить горизонтально з≥ швидк≥стю
, що летить горизонтально з≥ швидк≥стю  , попадаЇ в бал≥стичний ма€тник масою
, попадаЇ в бал≥стичний ма€тник масою  ≥ застр€Ї в ньому. Ќа €ку висоту
≥ застр€Ї в ньому. Ќа €ку висоту 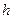 п≥дн≥метьс€ ма€тник п≥сл€ удару?
п≥дн≥метьс€ ма€тник п≥сл€ удару?
ƒано:



| —I


|
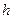 Ц? Ц?
|
јнал≥з

«апишемо закони збереженн€ к≥лькост≥ руху ≥ енерг≥њ з урахуванн€м умови задач≥: 1) удар непружний; 2) рух зд≥йснюЇтьс€ в одному напр€мку; 3) к≥нетична енерг≥€ повн≥стю переходить в потенц≥альну.

де  Ц швидк≥сть ма€тника з кулею.
Ц швидк≥сть ма€тника з кулею.
–озвТ€завши систему р≥вн€нь, одержимо:
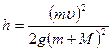 .
.
ќбчисленн€:
 .
.
¬≥дпов≥дь: висота, на €ку п≥дн≥метьс€ бал≥стичний ма€тник,  .
.
4.7. олесо, рад≥ус €кого  ≥ маса
≥ маса 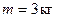 скочуЇтьс€ без терт€ по похил≥й площин≥ довжиною
скочуЇтьс€ без терт€ по похил≥й площин≥ довжиною  ≥ кутом нахилу
≥ кутом нахилу  . ¬изначити момент ≥нерц≥њ колеса, €кщо його швидк≥сть
. ¬изначити момент ≥нерц≥њ колеса, €кщо його швидк≥сть 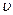 в к≥нц≥ руху р≥вна
в к≥нц≥ руху р≥вна  .
.
ƒано:

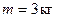



| —I
 
|
 Ц? Ц?
|
јнал≥з
 «а законом збереженн€ енерг≥њ маЇмо:
«а законом збереженн€ енерг≥њ маЇмо:
 .
.
ќск≥льки в умов≥ задач≥ задано л≥н≥йну швидк≥сть колеса, то використаши зам≥ну:  , одержимо
, одержимо  . ¬раховуючи, що
. ¬раховуючи, що  , маЇмо
, маЇмо

ќтже, 
ќбчисленн€:
 .
.
¬≥дпов≥дь: момент ≥нерц≥њ колеса  .
.
4.8. ƒва вантаж≥ масами  ≥
≥  зТЇднан≥ невагомою ниткою, перекинутою через блок масою
зТЇднан≥ невагомою ниткою, перекинутою через блок масою  . «найти прискоренн€
. «найти прискоренн€  , з €ким рухаютьс€ вантаж≥, ≥ силу нат€гу
, з €ким рухаютьс€ вантаж≥, ≥ силу нат€гу 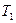 ≥
≥  нитки, до €коњ п≥дв≥шен≥ вантаж≥. Ѕлок вважати однор≥дним диском. “ерт€м знехтувати.
нитки, до €коњ п≥дв≥шен≥ вантаж≥. Ѕлок вважати однор≥дним диском. “ерт€м знехтувати.
ƒано:



|
 Ц? Ц?
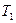 Ц? Ц?
 Ц? Ц?
|
 јнал≥з
јнал≥з
Ќа кожен ≥з вантаж≥в д≥ють дв≥ сили: сила т€ж≥нн€, €ка направлена вниз, ≥ сила нат€гу нитки, €ка направлена вгору. –≥внод≥йн≥ цих сил спричинюють р≥вноприскорений рух т≥л. «г≥дно з другим законом Ќьютона, маЇмо:

ќбертанн€ блоку в≥дбуваЇтьс€ зг≥дно основного закону динам≥ки обертального руху твердого т≥ла:
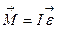 ,
,
де  , ≤=
, ≤=  . ¬раховуючи, що
. ¬раховуючи, що 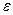 =
=  , де
, де  Ц рад≥ус блока, маЇмо
Ц рад≥ус блока, маЇмо
 або
або 

—проектувавши р≥вн€нн€ (1) ≥ (2) на в≥сь  ≥, додавши до них р≥вн€нн€ (3), отримуЇмо:
≥, додавши до них р≥вн€нн€ (3), отримуЇмо:
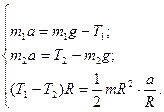
≤з перших двох р≥вн€нь системи визначаЇмо 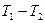 ≥ п≥дставл€Їмо у третЇ:
≥ п≥дставл€Їмо у третЇ:  «в≥дки
«в≥дки  :
:

« перших р≥вн€нь системи знаходимо сили нат€гу нитки:
 ;
;  .
.
ќбчисленн€:
 ;
;
 ;
;  .
.
¬≥дпов≥дь: прискоренн€, з €ким рухаютьс€ вантаж≥, 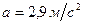 , сили нат€гу нитки в≥дпов≥дно:
, сили нат€гу нитки в≥дпов≥дно:  ≥
≥  .
.






