Стационарлы және стационарлы емес модельдер. Егер де φ оператордың түрі және оның p параметрлері уақыт бойынша өзгермесе, яғни келесі орындалса
φ[p(t),x]= φ[p(t+τ),x],яғниy= φ(p,x)
онда модель стационарлы болып табылады.
Егер де модель параметрлері уақыт бойынша өзгеретін болса
y= φ[p(t),x]
модель параметрлік стационарлыемес.
Уақыттан функция түрі де тәуелді болса, бұл жағдай стационарлы еместіктің ең жалпы түрі болады. Бұл кезде функцияға тағы бір аргумент қосылады:
y= φ(p,t,x)
Детерминді және стохастикалық модельдер түсініктемесі. Осы модельдер қандай математикалық теңдеулермен сипатталады?
Процесте кез келген кездейсоқ әсерлер жоқ деп есептелсе, процесс детерминерленген (анықталған) деп аталады; осындай процестерді бейнелейтін модельдер – детерминерленген модель болады.
Ықтималдық процестер мен оқиғаларды бейнелейтін модельдер стохастикалық модель деп аталады; бұл кезде кездейсоқ процестің бірсыпыра іске асырылуы болжанып, орта сипаттамалары бағаланады.
Здіксіз және дискретті модельдер түсініктемесі. Осы модельдер қандай математикалық теңдеулермен сипатталады?
Уақыт бойынша үздіксіз және дискретті модельдер. Үздіксіз модельдер жүйелердегі үздіксіз процестерді бейнелейді. Уақыт үздіксіз аргумент ретінде қарастырылатын объект күйін бейнелейтін модельдер уақыт бойынша үздіксіз модель болады:
y(t)=φ[p(t),x(t)], p(t)=ψ[y(t),x(t)].
Дискретті модельдер дискретті болып табылатын процестерді бейнелеуге қолданылады. Дискретті модель объект жүріс-тұрысын дискретті уақыттың аралықтарында болжай алмайды. Егер де уақыт бойынша ∆t қадамымен кванттауды еңгізсек, онда  шкала қарастырылады, мұнда i=0,1,2… дискретті уақыт мағынасы болады. Сонда дискретті модель келесі түрде болады:
шкала қарастырылады, мұнда i=0,1,2… дискретті уақыт мағынасы болады. Сонда дискретті модель келесі түрде болады:
y(i)=φ[p(i),x(i),∆t]; p(i)=ψ[x(i),y(i),∆t].
∆t қадамы дұрыс таңдалынса, дискретті модельден алдын ала берілген дәлдікпен нәтижені алуға болады. ∆t өзгерсе, айырымдық теңдеудің де коэффициенттері қайта есептелінуі керек.
Дискретті-үздіксіз модельдер. Егер де үздіксіз процестермен бірге объектте дискретті процестер бар екендігін көрсету керек болса, дискретті-үздіксіз модельдер қолданылады.
Басқару объекттерді модельдеудің аналитикалық амалын түсіндіріңіз. Аналитикалық жолмен моделдеуде қолданылатын негізгі физикалық заңдылықтарын атаңыз.
Модельді таңдағанда зерттелетін процестің жүріс-тұрысын анықтайтын физика-химия заңдылықтарды есепке алуда бірінші амал негізделген. Осындай модельдер аналитикалық модельдер деп аталады. Басқа сөзбен айтқанда, модель теңдеулерін алу үшін зат пен энергияны сақтау фундаменталды заңдылықтары қолданылады, объектте өтетін физикалық және химиялық процестерді теориялық анализдеп модель теңдеулері шығарылады. Мұнда тәжірибелерді өткізу керек емес, сондықтан процестері жақсы оқылған объекттері жобалау қадамында олардың статикалық және динамикалық сипаттамаларын анықтау үшін осы әдістерді қолдануға болады. Объектті толығымен бейнелеген кезде алынған жүйенің есебін табу өте қиын.
Екінші амал "қара жәшік" концепциясында негізделген, яғни объекттің ішкі құрамы белгісіз, одан да зор, зерттеушіге керек те емес деп есептелінеді. Барлық ақпарат объектті пассивті және активті тәжірибелерде бақылаудан алынады, басқа сөзбен айтқанда процесс қасиеттерін "кіріс -шығыс" қатынас арқылы бейнелеген жеткілікті деп есептелінеді.
Аналитикалық және тәжірибелік әдістер арасында ақпараттық жағынан және қолдану аймағы жағынан принципиалды айырмашылықтары бар. Аналитикалық әдістер екі сұраққа жауап бере алады: объекттің жүріс-тұрысы қандай және неге олай? Екінші түрдегі модельдер тек қана "қандай?" деген сұраққа жауап бере алады.
Аналитикалық әдістер эмпирикалық әдістерге қарағанда жалпы болып табылады және олардың көмегімен алынған нәтижелер фундаменталды болады. Бірақ бұл жеңіл берілмейді. Олар эмпирикалық әдістерге қарағанда күрделі және қиындықтар аналитикалық модельді құру кезінен бастап туады. Егер де объектті "қара жәшік" ретінде бейнелеу үшін статистика мен автоматты реттеу теориясынан білімдер жеткілікті болса, аналитикалық модельдерді құру үшін физика, химия, гидродинамика, т.б. пәндердің әртүрлі салаларынан білімдері мен түрлі-түрлі математикалық аппараты қажет. Сонымен бірге бұл қиындықтар аналитикалық модельдердің үлкен ақпараттық сыйымдылығымен орнын толтырады.
Динамика теңдеулерін қарапайымдылауға қандай амалдар қолданылады? Модельдерді сызықтандыру процедурасы. Cызықтандыру негізінде алынған модельдің орындалу аймағы.
Динамика теңдеулер жүйесі әдетте сызықты емес болғандықтан, оларды аналитикалық жолмен шешу жалпы кезде мүмкін емес. Сондықтан есеп спецификасына қарай теңдеулер және шектеулермен анықталатын кейбір байланыстарды жою үшін әртүрлі қарапайымдау әрекеттері орындалады. Сонымен бірге процестің маңызды қасиеттері сақталу керек.
Ең қарапайым (математикалық шешу жағынан) статикалық есеп болады. Уақыт және координаттар бойынша туындылар нөлге тең, сондықтан дифференциалдық теңдеулер орнына алгебралық теңдеулерді аламыз (жинақталған параметрлері бар объекттердің стационарлы режимдері).
Қарапайымдылық жағынан келесі стационарлық есеп болады. Теңдеулерде уақыт бойынша туындалар нөлге тең болады, сондықтан тәуелсіз координаттар саны азаяды. Стационарлы емес есептердің математикалық түрін қарапайымдау үшін өзара байланысқан жүйелер санын азайту, теңдеулер санын азайту жолымен, бөлек теңдеулердегі кейбір байланыстарды жою жолымен, кеңістік координаттар санын азайту және теңдеулерді сызықтандыру жолдарымен орындалады. Математикалық көзқарас жағынан жүйе бекітілмеген болады. Жойылған теңдеулерді процестің жүріс-тұрысын жуықтап көрсететін алгебралық тәуелділіктермен алмастыру керек. Мысалы, сәйкес параметрлері тұрақты деп есептелінуі мүмкін.
Көптеген практикалық жағдайларда нақты ағынның қозғалу заңдары тәжірибелік мәліметтер негізінде табылады. Тәжірибелік зерттеулерден ағынның нақты құрамын қамтып көрсететін кейбір коэффициенттері анықталады, мысалы, жылдамдық, температура, тығыздылықтың кеңістік бойынша өзгеретінін есепке алатын тәуелділіктер. Осындай коэффициенттері үйкелу, жылу беру, екі компоненттік қоспаларда фазалардың бір-бірі арқылы қозғалу жылдамдықтар, т.б. болып табылады. Олардың барлығы ағынның интегралдық сипаттамалары болады, олар анықталған жуықтаумен нақты ағындағы қозғалыс мөлшерімен, жылулықпен, затпен алмасуды қамтып көрсетеді. Аталған коэффициенттер көмегімен және ағын кесіндісі бойынша параметрлердің орта мәндерімен жылу беру, гидравликалық кедергі, фазалар таратылуы көрсетіледі. Олар арасындағы байланыстар да тәжірибеден табылады.
Эмпирикалық коэффициенттерді және аталған тәуелділіктерді қолдану ағынның нақты үш өлшемдігін қарастырмауға мүмкіндік береді. Сонда кейбір теңдеулер қарапайымдалады, кейбіреулерін жоюға болады. Осындай қарапайымдауды өткізуге болады, себебі эмпирикалық тәуелділіктер ағынның нақты үш өлшемділігін қамтып көрсетеді деп есептеуге болады. Кей кезде жоғарыда айтылған қорытындылар негізінде динамикалық сипаттамаларды есептеу үшін бір өлшемді модельді қолдануға болады, ал кейбір кезде жинақталған параметрлері бар модельді. Бір өлшемді модельдерде параметрлер тек қана ағын осімен бағытталған бір координата бойынша өзгереді. Канал кесіндісі бойынша параметрлер тұрақты болып орта мәнге тең деп есептелінеді.
Жинақталған параметрлері бар модельдерде жүйенің барлық параметрлері кеңістік координаталардан тәуелді емес, тек қана уақыт функциясы болады деп есептелінеді. Кеңістік координата бойынша туындылар функцияның кірудегі және шығудағы мәндерінің айырмашылығының канал ұзындығына қатынасымен алмасады.
Тұрақты жүйелерде өтпелі процестер барлық біртекті параллелді қосылған элементтерінде бірдей өтеді. Сондықтан өтпелі процестерді зерттегенде толық жүйені қарастырмай, тек қана жүйенің бір элементін қарастыруға болады.
Теңдеулерді сызықтандыру. Модельдерді қарапайымдаудың бір әдісі алынған теңдеуді сызықтандыру болады, басқа сөзбен айтқанда сызықты математикалық модельге көшу. Процестердің динамикасын модельдеудің соңғы мақсаты динамикалық сипаттамаларын анықтау үшін алған модельдерді басқару жүйелерде қолдану болып табылады. Сондықтан міндетті түрде теңдеулердің шешімін табу керек. Сызықты дифференциалдық теңдеулер жеңіл шешіледі. Бірақ объекттің жүріс-тұрысын әр кезде сызықты теңдеумен бейнелеу мүмкін емес. Сондықтан сызықты емес тәуелділіктер аргументтердің берілген диапазонында сызықты өрнектермен жуықталады. Басқа сөзбен айтқанда, кірудегі аргументтердің берілген диапазонында сызықты емес теңдеулер сызықты теңдеулермен алмастырылады, сызықтандырылады. Сызықты объектілерде кірудегі және шығудағы сигналдар арасындағы байланыс беріліс функциямен жеңіл бейнеленеді. Сызықтандыру әдетте сызықты емес теңдеулерді бастапқы стационарлы режим аймағында Тейлор қатарына жіктеу жолымен орындалады. Жіктеудің тек қана сызықты мүшелерін қалдырып, соңынан теңдеулерден статика теңдеулерін алып тастаймыз. Осы жолмен алынған объект моделі бастапқы стационарлы режимнен кіші ауытқуларда орындалады.
Модельдің дифференциалдық теңдеуін бейне кеңістігіндегі модельге түрлендіру үшін қандай процедура қолданылады? Мысал келтіріңіз.
Модельдің дифференциалдық теңдеуін бейне кеңістігіндегі модельге түрлендіру үшін Лаплас операторы қолданылады. Мысалы бір есеп құрастырайық.  ;
; 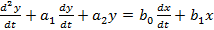 ;
;  ;
;
 ; Y(p)[
; Y(p)[  ;
;





