Задача о построении правильного 
-угольника равносильна задачи о делении окружности на равных частей. Если выбрать систему координат так, что начало координат, лежит в центре окружности, а точка (1,0) на окружности, то задача сводится к построению корней уравнения
,
причем исходным полем является поле рациональных чисел.
Построение правильных -угольников при =3,4,6 затруднений не вызывает. Ясно также, как построить правильный 2 -угольник, если задан или построен правильный -угольник; это задача сводится к делению дуги или хорды пополам.
Рассмотрим задачу о построении правильного пятиугольника. Как отмечалось выше, эта задача равносильна задаче построения корней уравнения 
.
Так как 
, то вопрос сводится к построению корней уравнения
(1)
Запишем это уравнение в виде
И положим 
. Тогда
и решение уравнения (1) сводится к последовательному решению уравнения
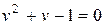(2)
а затем квадратных уравнений
,
где 
– оба корня уравнения (2).
Отсюда видно, что уравнения (1) разрешимо в квадратных радикалах и согласно Т2 § 11 все его корни можно построить циркулем и линейкой. Ясен также и путь построения: сначала построить корни
уравнения (2), а затем по имеющимся точкам 
и 
строить корни уравнений , 
.
Рассмотрим теперь случай 
. Здесь вопрос сводится к построению корней уравнения
(3)
Та же постановка дает
, 
и решение уравнения (3) сводится к решению уравнения
, (4)
а затем к решению уравнений
(5)
где 
– корни уравнения (4).
Уравнение (4) не имеет рациональных корней; поэтому многочлен 
неприводим над полем 
- алгебраические числа степени 3. В силу теоремы 1 § 11, 
построить невозможно. Но тогда и корни уравнения (3) тоже построить невозможно. В самом деле, если бы удалось построить корень 
уравнения (3), то для одного из корней имели бы место
,
а это означало бы, что корень уравнения (4) тоже можно построить.
Мы доказали невозможность построения циркулем и линейкой правильного семиугольника. Если имеет взаимно простые делители, то вопрос о возможности построения правильного -угольника сводится к вопросу о возможности правильных многоугольников с меньшим числом сторон.
Теорема 1. Если 
и числа 
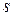и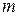 
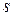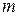взаимно просты, то окружность можно разделить циркулем и линейкой на равных частей, тогда и только тогда, когда она делится циркулем и линейкой и на и на равных частей.
Доказательство. Если окружность разделена на равных частей, то построен угол 
. Но тогда можно построить угол 
, и тем самым разделить окружность на 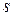равных частей, а также угол 
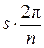и тем самым разделить окружность на 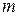равных частей.
Обратно, пусть окружность разделена и на 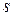; и на 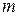– равных частей. Так как 
то существуют целые числа 
и 
, что
.
Отсюда 
или 
.
Последнее равенство показывает – как, имея углы 
и 
построить угол , т.е. разделить окружность на равных частей.
Мы рассматривали здесь некоторые частные случаи в задаче построения правильных многоугольников. Однако еще в начале прошлого века знаменитый математик К.ГАУСС дал полное решение этой задачи. Мы приведем его результаты без доказательства.
Все простые числа в последовательности 
, 
… называются простыми числами ФЕРМА. Сам Ферма показал, что все числа в этой последовательности являются простыми. Оказалось же, что уже при 
получается составное число. В настоящее время известно только 5 простых чисел Ферма, являющимися первыми пятью членами последовательности . Это число 3,5,17,257 и 65537. Одно из замечательных свойств простых чисел Ферма и составляет содержание основной теоремы Гаусса.
Теорема 2. Если 
- простое нечетное число, то правильный -угольник можно построить циркулем и линейкой тогда и только тогда, когда является простым числом Ферма. Правильный 
-угольник, где – простое число и 
построить невозможно. Из этой теоремы вытекает, например, возможность построения правильных -угольников при = 3,5,257,65537 и невозможность при =7,8,11,13,25,125 и т.д. и мы здесь его не приводим. На основании этой теоремы уже без труда доказывается более общий результат, который дает полное решение поставленной задачи.
Теорема 3. Правильный -угольник, можно построить циркулем и линейкой тогда и только тогда, когда разложение числа на простые сомножители имеет вид
,
где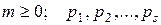 
– различные простые числа Ферма.
Доказательство. Множитель 
в разложении числа не влияет на разрешимость задачи; поэтому достаточно доказать теорему 3 для нечетного числа .
Пусть 
, где 
– различные простые числа Ферма. Согласно теореме 2 можно построить правильный 
-угольник при каждом 
. Но тогда в силу теоремы 1 можно построить и правильный - угольник.
Обратно, если можно построить правильные -угольники
,
где – нечетные простые числа, то в силу теоремы 1 можно построить правильный 
- угольник при каждом , а это означает согласно теореме 2, что при каждом имеем 
, 
– простое число Ферма.
ИСТОРИЧЕСКАЯ СПРАВКА
В настоящее время построены все известные многоугольники, число сторон которых есть простое число Ферма. 257-угольник построил Ришело (80 стр. текста), а 65537-угольник – Гермес (рукопись занимает огромный чемодан, который хранится в Гёттингенском университете). Способ построения тот же, который использовал Гаусс для построения 17-угольника.
Гаусс, сделавший много крупных открытий в самых различных областях математики, очень ценил свою первую научную работу о 17-угольнике, которую он выполнил в 1796г (через 5лет дал полное решение задачи о возможности построения правильного многоугольника циркулем и линейкой). Памятник, воздвигнутый на его могиле в Гёттингене, находится на пьедестале, имеющем форму 17-угольной призмы.
