Критерий разрешимости задач на построение, указанный в теореме § 10, практически не всегда удобен. Мы укажем более простые признаки, вытекающие из этой теоремы.
Теорема 1. Если число 
можно построить циркулем и линейкой, исходя из множество чисел 
, то является алгебраическим относительно исходного поля 
числом степени 
, 
Доказательство непосредственно следует из упомянутой выше теоремы §7 и св. 3 
§9.
Теорема 1 выражает необходимый признак разрешимости задач на построение. Если число не является алгебраическим относительно исходного поля или – алгебраическое, но его степень над полем отлична от , 
, то это число циркулем и линейкой построить невозможно.
В качестве примера на применение теоремы 1 рассмотрим три древние задачи: квадратура круга, удвоение куба и трисекции угла. Многочисленные и безуспешные попытки решить эти задачи и привели к возникновению теории геометрических построений.
1. Задача о квадратуре круга. С помощью циркуля и линейки построить квадрат, равновеликий заданному кругу. Выберем систему координат так, что начало лежит в центре заданного круга, а точка (1,0) на окружности. Тогда исходное поле совпадает с полем рациональных чисел. Площадь круга равна 
и, следовательно, длина ребра искомого квадрата равна 
. Так как и – трансцендентные числа, то в силу теоремы 1 построение ребра, а, следовательно, и самого квадрата, невозможно.
Задачу о квадратуре круга, имеющую 2-х тысячелетнюю историю, решал еще Архимед (3в. до н.э.). Впервые предположения о невозможности построения были высказаны в ХV (Леонардо да Винчи и др.). Многочисленная кагорта “квадратистов включала ” не только ученых математиков, но и часть людей, не связанных с математикой (делитантов). Это с чрезвычайно простой постановкой задачи. В связи с большим наплывом “решений” задачи при Французской академии наук была создана специальная комиссия по рассмотрению этих решений. Но поскольку наплыв “решений” не ослабевал, комиссия была ликвидирована, С “квадратистами” было покончено в 1882г. после того, как Линдеман доказал трансценденетность числа .
Задача об удвоении куба.
 | |||
 | |||
(0,0) 1
или 
Построить ребро куба, объем которого в два раза больше объема заданного куба.
Выберем систему координат так, чтобы концы ребра заданного куба лежали в точках (0,0) и (1,0), а длину искомого куба обозначим через . Исходным полем снова будет поле рациональных чисел, а задача сводится к построению действительного корня многочлена 
. Этот многочлен по признаку Эйзенштейна неприводим над полем 
и поэтому все его корни являются алгебраическими числами степени 3. Так как 
, то такие корни построить невозможно.
Задача о трисекции угла.
1
, 
Задача свелась к построению уравнения
(1)
При 
, 
, поэтому уравнение (1) разрешимо в квадратных радикалах.
Если , то 
получим уравнение 
, 
(2)
Это уравнение неразрешимо в квадратных радикалах, т.к. множество 
не имеет радикалов.
Дан угол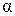 
. Построить 
.
Угол можно построить тогда и только тогда, когда число 
можно построить на основании заданного числа 
, но так как 
, то
Задача свелась к построению корней уравнения
,
когда задано число 
. Положим 
. Тогда 
и исходным полем является поле . Уравнение 
, как нетрудно проверить, не имеет радикальных корней, и потому многочлен 
неприводим над полем Q. Но тогда все его корни есть алгебраические числа степени 3 и один из них невозможно построить циркулем и линейкой. Значит, угол 
невозможно разделить на три равные части. Так как частный случай задачи неразрешим, то и сама задача неразрешима. Но в некоторых частных случаях (например, при , 
) эта задача разрешима.
Укажем один достаточный признак разрешимости задач на построение.
Теорема 2. Если алгебраическое уравнение
(1)
с действительными коэффициентами разрешимо в квадратных радикалах, что все его корни можно построить циркулем и линейкой исходя из множества 
.
Действительно, если уравнение (1) разрешимо в квадратных радикалах, то по теореме 1 § 9 все его корни принадлежат области рациональности 
или некоторому пифагорову расширению этого поля. Но так как является также исходным полем множества 
, то в силу теоремы § 10 все корни можно построить.
Упражнения.
1.Можно ли разделить на три равные части углы 
и 
?
2.Можно ли построить циркулем и линейкой точки пересечения кривых:
a)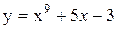 
и 
б) 
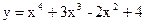и 
Решение:
a) 
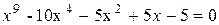не приводим по критерию Эйзейштейна 
б) 
– биквадратное уравнение – можно
