Поле алгебраических чисел и его замкнутость
Обозначим через  – множество всех чисел, алгебраических относительно поля
– множество всех чисел, алгебраических относительно поля  . Ясно, что
. Ясно, что 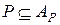 , точно также любое простое (а, следовательно, и составное) алгебраическое расширение поля
, точно также любое простое (а, следовательно, и составное) алгебраическое расширение поля  является подмножеством множества
является подмножеством множества 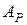 .
.
Теорема 1. Множество 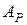 всех чисел, алгебраических относительно поля
всех чисел, алгебраических относительно поля  , является подполем поля
, является подполем поля  .
.
Доказательство. Пусть 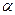 и
и  - любые элементы множества
- любые элементы множества 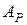 . Так как
. Так как 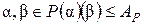 и
и 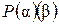 является полем, что
является полем, что 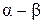 ,
, 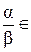
 Это значит, что
Это значит, что 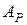 замкнуто относительно вычитания и деления, т.е. подполем поля
замкнуто относительно вычитания и деления, т.е. подполем поля  .
.
Определение. Множество всех чисел, алгебраических относительно поля  , называется полем алгебраических чисел над полем
, называется полем алгебраических чисел над полем  . Если
. Если 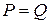 , то это множество называют просто полем алгебраических чисел.
, то это множество называют просто полем алгебраических чисел.
Теорема 3. Если над полем  существует неприводимый многочлен любой степени (как, например, над полем
существует неприводимый многочлен любой степени (как, например, над полем  ), то поле
), то поле 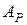 алгебраических над полем
алгебраических над полем  чисел не является конечным расширением поля
чисел не является конечным расширением поля  .
.
Действительно, предположим, что 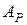 является конечным расширением поля
является конечным расширением поля  степени
степени  . Точка для любого числа
. Точка для любого числа  из
из 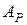 система
система 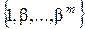
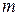 линейно зависима в
линейно зависима в 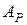 над
над  и, следовательно, степень
и, следовательно, степень  не превышает
не превышает  . Но это означает, что все многочлены степени
. Но это означает, что все многочлены степени 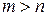 приводимы в кольце
приводимы в кольце 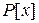 : получили противоречие.
: получили противоречие.
Следствие. Поле алгебраических чисел – бесконечномерное пространство над полем  . Если же над полем
. Если же над полем  существуют неприводимые многочлены степени
существуют неприводимые многочлены степени  , а все многочлены степени
, а все многочлены степени 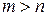 приводимы, то этого утверждать уже нельзя. Например, поле
приводимы, то этого утверждать уже нельзя. Например, поле  является полем алгебраических чисел над полем
является полем алгебраических чисел над полем 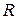 . В тоже время
. В тоже время  – простое алгебраическое расширение поля
– простое алгебраическое расширение поля 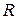 (
(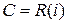 ), причем размерность
), причем размерность  над полем
над полем 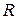 равна 2.
равна 2.
Теорема 2. Поле 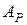 алгебраических над полем
алгебраических над полем  чисел алгебраически замкнуто, т.е. все корни многочлена степени
чисел алгебраически замкнуто, т.е. все корни многочлена степени 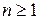 из кольца
из кольца  принадлежат полю
принадлежат полю 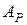 .
.
Доказательство. Пусть 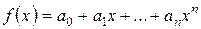 – любой многочлен из кольца
– любой многочлен из кольца  ,
, 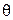 - любой корень этого многочлена. Требуется доказать, что
- любой корень этого многочлена. Требуется доказать, что 
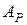 .
.
Очевидно, что 

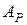 , а число
, а число 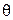 - алгебраично над полем
- алгебраично над полем 
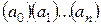 . Но тогда
. Но тогда 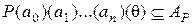 и, следовательно,
и, следовательно, 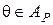 .
.
Заметим, что здесь использовался тот факт, что при определении составного алгебраического расширения не требуется алгебраичность 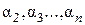 над полем
над полем  .
.
В связи с теоремой 2 полезно подчеркнуть, что 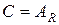 , а алгебраическая замкнутость поля
, а алгебраическая замкнутость поля  доказывалась и ранее – она вытекает из основной теоремы алгебры.
доказывалась и ранее – она вытекает из основной теоремы алгебры.
Упражнения.
1. Привести пример такого поля  , что поле
, что поле 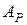 алгебраично над полем
алгебраично над полем  чисел является конечным расширением поля
чисел является конечным расширением поля  .
.
2. Доказать: если  – наивысшая степень неприводимых в кольце
– наивысшая степень неприводимых в кольце 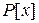 многочленов, то
многочленов, то 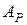 является конечным расширением поля
является конечным расширением поля  степени
степени  .
.
3. Доказать, что поле алгебраических чисел счетно.
Понятие о разрешимости уравнений в радикалах.
Определение 1. Говорят, что число  выражается в радикалах (в квадратных радикалах) через числовое множество
выражается в радикалах (в квадратных радикалах) через числовое множество  , если
, если  можно представить через элементы множества
можно представить через элементы множества  с помощью конечного числа арифметических операций (сложения, вычитания, умножения, деления) и операций извлечения корня (квадратного корня).
с помощью конечного числа арифметических операций (сложения, вычитания, умножения, деления) и операций извлечения корня (квадратного корня).
Например, число  , где имеются в виду арифметические корни, выражается в радикалах через множество
, где имеются в виду арифметические корни, выражается в радикалах через множество  . Так как это число представлено в виде
. Так как это число представлено в виде 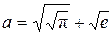 , то оно выражается даже в квадратных радикалах через множество
, то оно выражается даже в квадратных радикалах через множество  .
.
Заметим, что операция извлечения корня неоднозначна и поэтому разные числа могут одинаково выражаться в радикалах через одно и тоже множество
Например, все три корня кубического уравнения 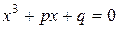 одинаково выражаются в радикалах через коэффициенты по формуле Кардано.
одинаково выражаются в радикалах через коэффициенты по формуле Кардано.
Укажем некоторые свойства понятия выражения в радикалах.
1. Всякое число из множества  выражается в радикалах множество
выражается в радикалах множество  . Например, число
. Например, число  выражается в радикалах через множество
выражается в радикалах через множество  .
.
2. Каждое рациональное выражается в радикалах через любое множество  .
.
Например, число 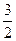 выражается через множество
выражается через множество  в виде
в виде 
Заметим, что в выражении чисел 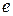 и
и 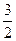 через множество
через множество  операция извлечения корня не используется. В таких случаях говорят, что число выражается через множество
операция извлечения корня не используется. В таких случаях говорят, что число выражается через множество  рационально.
рационально.
3. Если  выражается в радикалах через множество
выражается в радикалах через множество  , а каждый элемент из
, а каждый элемент из  , выражается в радикалах через множество
, выражается в радикалах через множество  , то
, то  – выражается в радикалах через
– выражается в радикалах через  .
.
4. Если  выражается в радикалах через множество
выражается в радикалах через множество  и
и 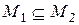 , то
, то  выражается в радикалах через
выражается в радикалах через  .
.
5. Число  выражается в радикалах через конечное множество
выражается в радикалах через конечное множество  тогда и только тогда, когда
тогда и только тогда, когда  выражается в радикалах через поле
выражается в радикалах через поле 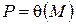 .
.
Свойства 1-4 очевидны, докажем свойство 5.
Если  выражается в радикалах через множество
выражается в радикалах через множество  , то тоже в силу свойства 4 выражается в радикалах и через множество
, то тоже в силу свойства 4 выражается в радикалах и через множество 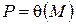 , содержащее подмножество
, содержащее подмножество  . Обратно, пусть
. Обратно, пусть  выражается в радикалах через поле
выражается в радикалах через поле 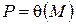 . Согласно теореме 2 §6 и свойству 2 каждый элемент из поля
. Согласно теореме 2 §6 и свойству 2 каждый элемент из поля  выражается в радикалах (и даже рационально) через множество
выражается в радикалах (и даже рационально) через множество  . Но тогда по свойству 3 и число
. Но тогда по свойству 3 и число  выражается в радикалах через множество
выражается в радикалах через множество  .
.
Свойства 1-5 будут справедливы и в том случае, когда всюду слово «выражается в радикалах» заменить словами «выражается в квадратных радикалах»
Напомним, что поле  является подполем любого числового поля. Поэтому составное расширение можно определить и иначе: это есть пересечение всех числовых полей, содержащих подмножество
является подполем любого числового поля. Поэтому составное расширение можно определить и иначе: это есть пересечение всех числовых полей, содержащих подмножество  .
.
Определение 2. Уравнение
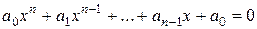 (1)
(1)
называется разрешимым в радикалах (в квадратных радикалах) если каждый корень этого уравнения выражается в радикалах (в квадратных радикалах) через множество  .
.
Определение 3. Составное расширение  называется областью рациональности уравнения (1).
называется областью рациональности уравнения (1).
Из свойства 5 вытекает следующая теорема.
Теорема 1. Уравнение (1) разрешимо в радикалах (в квадратных радикалах) тогда и только тогда, когда каждый корень этого уравнения выражается в радикалах (в квадратных радикалах) через область рациональности этого уравнения.
Ясно, что линейные, квадратные и биквадратные уравнения разрешимы только в радикалах, но и в квадратных радикалах. Уравнения 3 и 4-ой степени разрешимы в радикалах, но не всегда разрешимы в квадратных радикалах. Вопрос о разрешимости в радикалах уравнений выше 4-й степени оказался весьма трудным. Только в начале ХХ1 века норвежский математик Н.АБЕЛЬ (1802-1829 г.г.) установил, что для уравнения 5 степени не существует формулы, подобной формуле КАРДАНА для уравнений 3-ей степени, которая бы выражала корни данного уравнения через коэффициенты. Значительно дальше продвинулся в этом направлении французский математик Э.ГАЛУА (1811-1832г.г.) Используя понятие группы, он исследовал условия разрешимости в радикалах уравнений выше 4-ой степени.




