Разрешимость алгебраических уравнений в квадратных радикалах имеет важное значение в теории геометрических построений циркулем и линейкой и тесно связано с понятием пифагорово расширения.
Определение 1. Простое алгебраическое расширение  где
где  ,
,  , называется простым пифагоровым расширением поля
, называется простым пифагоровым расширением поля  .
.
Определение 2. Если в цепочке полей
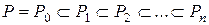
каждое поле является простым пифагоровским расширением предшествующего ему соседнего поля, то есть,

то поле  при любом
при любом 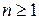 называется пифагоровым расширением поля
называется пифагоровым расширением поля  .
.
Отметим ряд простейших свойств пифагоровых расширений.
1. Простое пифагорово расширение  состоит из всевозможных чисел вида
состоит из всевозможных чисел вида  , где
, где  .
.
Это свойство вытекает из теоремы 2, §3.
2. Пифагорово расширение  является конечным расширением поля
является конечным расширением поля  степени
степени 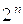 . Это есть частный случай теоремы 1 § 5.
. Это есть частный случай теоремы 1 § 5.
3. Каждый элемент из пифагорова расширения  является алгебраическим относительно поля
является алгебраическим относительно поля  числом степени
числом степени 
 .
.
Доказательство следует из свойства 2 и т.3 § 3 (в старом варианте теорема 2 и замечание к теореме 2 § 3).
Теорема 1. Число  выражается в квадратных радикалах через
выражается в квадратных радикалах через  тогда и только тогда, когда
тогда и только тогда, когда  принадлежит некоторому пифагорову расширению поля
принадлежит некоторому пифагорову расширению поля  .
.
Доказательство. Сначала индукцией по  покажем, что любой элемент из поля
покажем, что любой элемент из поля  выражается в квадратных радикалах через
выражается в квадратных радикалах через  . Так как для любого
. Так как для любого  из поля
из поля 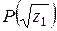

 ,
, 
то при 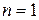 наше утверждение верно.
наше утверждение верно.
Предположим, что наше утверждение верно при 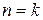 , т.е. каждый элемент из
, т.е. каждый элемент из  выражается в квадратных радикалах через
выражается в квадратных радикалах через  . Тогда, если
. Тогда, если  , то
, то
 , где
, где 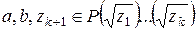
Это значит, что  выражается в квадратных радикалах через
выражается в квадратных радикалах через  . Отсюда, учитывая предположение индукции и свойства 3 § 8, заключаем, что
. Отсюда, учитывая предположение индукции и свойства 3 § 8, заключаем, что  выражается в квадратных радикалах через
выражается в квадратных радикалах через  , т.е. наше утверждение верно при
, т.е. наше утверждение верно при 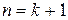 . Но тогда оно верно и при любом натуральном значении
. Но тогда оно верно и при любом натуральном значении  .
.
Обратно, если число  выражается в квадратных радикалах через
выражается в квадратных радикалах через  , то последовательно присоединяя эти радикалы, мы и получим пифагорово расширение поля
, то последовательно присоединяя эти радикалы, мы и получим пифагорово расширение поля  , содержащее
, содержащее  .
.
Например, если  , где
, где 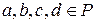 , то
, то  принадлежит составному алгебраическому расширению
принадлежит составному алгебраическому расширению
 , где
, где  .
.
Если  , то это и есть искомое пифагорово расширение. Если же, например,
, то это и есть искомое пифагорово расширение. Если же, например, 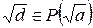 , то искомым пифагоровым расширением будет поле
, то искомым пифагоровым расширением будет поле  .
.
Следствие. Уравнение

разрешимо в квадратных радикалах тогда и только тогда, когда все его корни принадлежат некоторому пифагорову расширению области рациональности этого уравнения.
Доказательство вытекает из Т1 и Т1 § 8.
Теорема 2. Кубическое уравнение
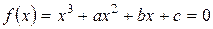 (1)
(1)
разрешимо в квадратных радикалах  , когда, по крайней мере, один его корень принадлежит области рациональности
, когда, по крайней мере, один его корень принадлежит области рациональности 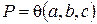 .
.
Доказательство. Если 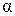 – корень уравнения (1),
– корень уравнения (1),  , то
, то
 ,
,  .
.
Отсюда уже видно, что все корни уравнения (1) выражаются в квадратных радикалах через поле  и в силу теоремы 1 § 8 уравнение (1) разрешимо в квадратных радикалах.
и в силу теоремы 1 § 8 уравнение (1) разрешимо в квадратных радикалах.
Обратно, пусть уравнение (1) разрешимо в квадратных радикалах. Тогда все его корни принадлежат некоторому пифагорову расширению поля  и, следовательно, являются алгебраическими над полем
и, следовательно, являются алгебраическими над полем  числами степени
числами степени  . Отсюда и следует, что, по крайней мере, один из корней принадлежит полю
. Отсюда и следует, что, по крайней мере, один из корней принадлежит полю  . В самом деле, если бы ни один из корней не принадлежал полю
. В самом деле, если бы ни один из корней не принадлежал полю  , то многочлен
, то многочлен  был бы неприводим над полем
был бы неприводим над полем  , и все его корни были бы алгебраическими над полем
, и все его корни были бы алгебраическими над полем  числами степени
числами степени 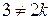 .
.
Следствие. Кубическое уравнение с рациональными коэффициентами разрешимо в квадратных радикалах тогда и только тогда, когда, оно имеет по крайней мере один рациональный корень.
Упражнения.
1. Какие из следующих уравнений разрешимы в квадратных радикалах:
a) 
b) 
c) 
d) 
2. Показать, что уравнение
 ,
,
не имеющее корней в области рациональности, разрешимо в квадратных радикалах тогда и только тогда, когда в области рациональности этого уравнения находится по крайней мере один корень кубической резольвенты.




