Законы постюения зеркальных отражений и анализ перспективных изображений в искусстве

1. Построение отражений в зеркальной поверхности

Отражения в зеркальной поверхности при умелом использовании мо­гут быть элементами композиции и сюжета картины. Зеркальное отраже­ние интерьера выявляет особенности архитектуры помещений, глубину пространства, поскольку на картине видно даже то, что находится за зри­телем. Этот прием использовал Веласкес на картине «Менины», где на зад­ней стене помещения в зеркале отражена королевская пара, которая ему позировала. Мир роскошного ресторана отражен в зеркале за спиной молодой женщины на картине Эдуарда Мане «Бар в Фоли-Бержер». Отра­жение предметов в спокойной глади воды, подчеркивает красоту пейзажа и усиливает его эмоциональное воздействие. Примерами служат картины В.Э. Борисова-Мусатова «Водоем», В.М. Васнецова «Аленушка», А.А. Ива­нова «Явление Христа народу».

Законы зеркальных отражений необходимо знать и внимательно наблю­дать при рисовании с натуры.

Лучи света, падающие на матовую поверхность, отражаются под угла­ми с микроскопическими отклонениями, что сразу влияет на восприятие данного предмета. Чем меньше шероховатость поверхности, тем более упо­рядочен поток отраженных лучей, тем вероятнее получение отражения. На металлических предметах хорошо просматриваются очертания отражен­ного предмета, но плохо видны его детали. Сила света отраженных лучей будет тем сильнее, чем ярче источник света.

Лучи света, попадая на зеркальную поверхность, изменяют свое на­правление. Построение изображений лучей света, отраженных от плос­кой зеркальной поверхности (рис. 279), основано на следующих законах оптики:

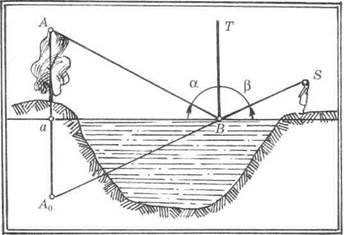
Рис. 279

1. Лучи, падающий (АВ) и отраженный (BS), расположены в одной плос­кости с перпендикуляром (ВТ), проведенным к зеркалу через точку паде­ния (В).

2. Угол падения (а) равен углу отражения (Р).

Рассмотрим закономерность образования отражений в зеркальной по­верхности. Если провести плоскость, параллельную картинной, через вер­шину дерева — точку А, луч, падающий от точки А на поверхность воды под углом а к перпендикуляру ВТ, отразится под тем же углом и попадет в глаз наблюдателя в точке S. Отражение А₀ окажется на продолжении отра­женного луча SB ниже уровня зеркальной поверхности на величину отрез­ка аА. Образовавшиеся прямоугольные треугольники ВаА и ВаА₀ будут рав­ны, так как имеют по два одинаковых катета. Следовательно, изображе­ния предметов в зеркальной поверхности располагаются ниже уровня зеркала в перевернутом виде на расстоянии, равном расстоянию от этих предметов до зеркала, т. е. симметрично.

Зеркала относительно картинной и предметной плоскости могут распола­гаться по-разному. Наиболее часто встречаются следующие положения:

— горизонтальное — зеркало параллельно предметной и перпендику­лярно к картинной плоскости;

— фронтальное — зеркало параллельно картинной и перпендикулярно к предметной плоскости;

— вертикальное — зеркало перпендикулярно к предметной плоскости и под произвольным углом наклонено к картине.

Отражение предмета в спокойной глади воды —пример естественного горизонтального зеркала природы. Построим отражение предмета призма-

Рис. 280

тической формы АаВЬ и точки К, расположенных на берегу (рис. 280). Нач­нем построение с ребраАа, как наиболее приближенного к краю воды и про­ведем через него вспомогательную вертикальную плоскость Р, совпадаю­щую с гранью АаЪВ и сходящуюся в точке F_t. Построим на плоскости Р ли­нию раздела земли и воды a₁F₁. Согласно закону отражения Аа_г = а_гА*. Стороны объекта и их отражения сходятся в соответствующие точки схода F_l~n F₂. В зависимости от расположения объектов одно отражение может перекрывать другое. В нашем примере построенная точка В* будет перекры­та отражением набережной. Найдем отражение точки К, для этого восполь­зуемся точкой схода F₂ и проведем вспомогательную плоскость. Из точки К опустим перпендикуляр и отложим на нем расстояние Kh_x = к_гК„.

На картине (рис. 281) изображена набережная, расположенная под про­извольным углом к зрителю. На ней находятся павильон и осветительные столбы, а в воде отражаются все предметы. Несмотря на разворот изобра­жения, правила построения останутся прежними — для построения отра­жения предмета в зеркальной поверхности из всех характерных точек пред-

Рис. 281

мета опустим перпендикуляры к плоскости зеркала. На каждом перпенди­куляре найдем точку раздела и от нее отложим расстояние, на какое уда­лен данный элемент.

Отражение в горизонтальном зеркале равно отражающемуся предмету и подчинено тем же законам перспективного изображения, что и сам предмет.

Вертикальные зеркала используют как в жилых, так и общественных помещениях. Большие зеркальные поверхности визуально расширяют гра­ницы интерьеров и придают им парадность и монументальность.

На картине (рис. 282) изображено зеркало, перпендикулярное к пред­метной и картинной плоскостям, т. е. расположенное на боковой стороне стены, а также вертикальный отрезок АВ. Требуется построить отражение отрезка в зеркале.

Через концы отрезка, т. е. точки А и В проведем горизонтальные пря­мые, перпендикулярные к плоскости зеркала. Проведенные прямые обра­зуют фронтальную плоскость, которая пересечет зеркало по перпендику­ляру 1-2. От прямой 1-2 в глубину зеркала отложим отрезки 1А и 2В, т. е. расстояние от заданного отрезка до зеркала. Полученные в зеркале точки А* и В* соединим прямой, получим отрезок А*В*— отражение отрезка АВ в зеркале.

Рис. 282

Рис. 283

Зеркало расположено фронтально (рис. 283) и необходимо построить отражение отрезка АВ.

Используем масштаб глубин. Через концы отрезка проведем две парал­лельные прямые, сходящиеся в точку Р, т. е. горизонтально проецирую­щую плоскость, перпендикулярную к зеркалу. Построим линию пересече­ния зеркала с проецирующей плоскостью, т. е. прямую 3-4. С помощью ди-

станционной точки определим по масштабу глубин расстояние от отрезка АВ до зеркала, получим отрезок В1. От точки 1 вправо отложим отрезок, равный отрезку В1, получим отрезок 1-2. Точку 2 соединим с дистанцион­ной и получим основание отражения отрезка, т.е. точку Б*. Из нее прове­дем вертикальную прямую до пересечения с прямой ЗР в точке А*. Отрезок А*Б*— отражение отрезка АВ.

Существует еще один несложный способ построения отражения в зер­кале (рис. 284). Отрезок заключим в глубинную плоскость, соединим кон­цы отрезка А и Б с главной точкой картины и найдем линию пересечения вновь введенной плоскости с зеркалом. Отрезок 1-2 делим пополам 1С = С2. Через середину проведем диагонали, которые определят сторону А*Б* квад­рата АВБА*.

На картине (рис. 285) задан интерьер комнаты. На фронтальной стене комнаты расположено зеркало. Пол покрыт квадратным паркетом, на сте­нах развешаны картины разных размеров, у левой стены стоит скамейка, а по середине подиум с вазой. Требуется построить отражение предметов, на­ходящихся в этом помещении.

Определим общие размеры отражения комнаты и рисунок паркетных плит. Для этого продолжим линии плинтусов и карнизов в точку Р. С помо­щью дробной дистанционной точки определим глубину отражения комна­ты. Отражение всех остальных предметов построим на основе вышеприве­денных примеров.

Зеркало расположено вертикально, но под произвольным углом к кар­тине (рис. 286). Чтобы построить отражение отрезка АВ горизонтальный

Рис. 285

след плоскости зеркала продолжим до пересечения с линией горизонта в точке F₂. Точку F_z соединим прямой с верхней линией зеркала. На картине при совмещенной точке зрения S_k построим прямой угол F₂S_kF₁. Через кон­цы отрезка АВ проведем прямые в точку F_t. Плоскость ABF_X будет перпен­дикулярна к плоскости зеркала, поскольку плоскость зеркала и плоскость ABF_l проходят через общий перпендикуляр 1-2 к предметной плоскости — линия пересечения плоскости зеркала с плоскостью ABF^ Отложим от пря­мой 1-2 в глубину отрезок, равный отрезку 2-3. Для этого на линии горизон­та возьмем произвольную точку Е и соединим ее с точкой В. Проведем гори­зонтальную прямую, проходящую через точку 2. Эта прямая пересечется с прямой BF в точке 3. Отрезок 2-3 отложим на горизонтальной прямой от точ­ки 2 в глубину зеркала. Из полученной точки 3₁ проведем прямую в точку Е. Прямая З_гЕ пересечется с прямой BF_X в точке В*. Из нее восстановим перпен­дикуляр до пересечения с прямой AF_X в точке А*. Полученный отрезок А*В* — отражение отрезка АВ в зеркале. Из построения видно, что отраженный отре­зок получится уменьшенным за счет перспективного сокращения.

Аналогично выполнено построение отражения в зеркале угловой перс­пективы комнаты, на одной стороне которой располагается два полуоваль­ных окна (рис. 287).

Построим отражение вазы в вертикальном произвольно расположен­ном зеркале (рис. 288). Введем горизонтально-проецирующую плоскость и

 

Рис. 286

Рис. 287 202

Рис. 289

найдем линию пересечения ее с поверхностью зеркала — 7-6. От прямой 7-6, отложим все расстояния вглубь зеркала. Найдем ось вращения вазы, для чего отложим равные отрезки 1-7 = 7-1 * и восстановим перпендикуляр.

Соединив прямой точку 5 с точкой схода F,, на месте пересечения с перпен­дикуляром получим точку 5*.

Можно построить ось и способом, показанным на рис. 284. Для получе­ния контура вазы необходимо построить очерковые точки, определяя каж­дый раз направление и расстояние до зеркала (рис. 289).

►

Отражение в вертикальных зеркалах всегда расположено на том же рас­стоянии от зеркала, что и сам отражающийся предмет.

2. Перспективные изображения в картинах художников

Рис. 290 204

В истории изобразительного искусства сохранилось немало примеров, которые позволяют проследить процесс создания известных картин худож­ников от первых схематичных рисунков до окончательной реализации за­мысла. Изучение подготовительных эскизов показывает, как художник использует не только цветовые и тоновые средства, но и перспективные построения. Интересны подготовительные рисунки В.И. Сурикова к кар­тине «Боярыня Морозова» (рис. 290). Художник воспользовался известным

способом изображения перспективных линий для направления внимания зрителя на определенное место картины — на композиционный центр. Как бы мы не рассматривали эту картину, взгляд обязательно пролетит по до­роге к саням и остановится на лице и руке боярыни.

Другой распространенный прием можно наблюдать в картине И.И. Фир-сова «Юный живописец». Для того, чтобы акцентировать внимание зрителя на композиционном центре картины, художник размещает его в главной точ­ке картины, куда сходятся глубинные прямые. По этой же схеме написаны картины Ф.М. Славянский «На бал коне», В. И. Суриков «Меньшиков в Бере-зове». Начинающему художнику и педагогу очень полезно изучать эскизы к знаменитым картинам и исследовать путь, по которому художник прошел, создавая то или иное произведение искусств. Не менее полезно анализировать перспективные построения картин и знать некоторые теоретические положе­ния, по которым определяют ее основные элементы.

Перспективный анализ — проверка формы и размеров изображаемых предметов, их положения относительно картины и предметной плоскости, взаимного расположения персонажей, связанных единством действий при выбранных художником параметрах перспективного изображения. Перс­пективный анализ осуществляют в следующей последовательности:

1. Найдем положение линии горизонта, главной точки картины.

2. Найдем положение точки зрения и величину угла зрения.

3. Определим перспективные масштабы в картине.

4. Проверим изображение формы и размеров предметов.

5. Проведем реконструкцию какого-либо предмета в картине.

Наиболее точный перспективный анализ возможен в тех случаях, ког­да художник в работе целенаправленно пользовался законами линейной перспективы.

Для анализа наиболее удобны те произведения живописи, на которых изображены предметы четкой геометрической формы: квадраты, прямо­угольники, эллипсы, как изображение окружности в перспективе, или име­ющие параллельные прямые или прямой угол. Они помогают восстановить основные элементы картины.

Проведем перспективный анализ нескольких известных работ худож­ников. Определим линию горизонта и главную точку картины на схеме ра­боты Д.Г. Левицкого «Портрет Демидова» (рис. 291). Русский аристократ и меценат изображен на открытой террасе своего дома. Половицы на полу — горизонтальные параллельные линии, перпендикулярные картинной плос­кости, т. е. глубинные. Продолжение их позволяет определить главную точ­ку картины, а значит и положение линии горизонта. Она находится на уровне глаз портретируемого человека, из этого следует, что художник писал пор­трет стоя. Все построения показаны на уменьшенной схеме. Продолжение сторон стула позволяет определить точки схода F_x и F₂ и полуокружность, на которой лежит совмещенная точка зрения S_k.

Рис. 291 Положение главной точки картины можно определить и по предметам с прямыми углами. Если одна сторона прямого угла параллельна основа­нию картины, то предельной точкой его второй стороны будет главная точ­ка картины. Если фигура на картине является квадратом, то ее диагональ в пересечении с линией горизонта определит положение дистанционной точки, как показано на схеме с картины Яна Ван Эйка «Мадонна канцлера

Ролена» (рис. 292).

Аналогично определяют основные элементы картины, если квадрат расположен вертикально и перпендикулярно к картинной плоскости — две стороны квадрата вертикальны и параллельны боковым сторонам карти­ны как показано на схеме с картины испанского художника Диего Велас-киса «Менины» (рис. 293). На уменьшенной схеме видно, что горизонталь­ные стороны квадрата определяют главную точку картины Р, через кото­рую проходит линия горизонта.

Положение дистанционной точки можно определить двумя способами:

1. С помощью масштаба глубин. Отложим от точки А на горизонталь­ной прямой АВ, сторону квадрата. Пересечение прямой Bfi с линией гори­зонта определит дистанционную точку D₂.

2. С помощью диагонали квадрата. Через вершину ВС квадрата прове­дем диагональ. Точка пересечения ее с линией главного вертикала опреде­лит совмещенную точку зрения S_k и дистанционное расстояние PD₁ - PD₂.

 

Рис. 292

Рис. 293

Воспользуемся приемом, который предлагал А.П. Барышников для определения величины угла зрения при перспективном анализе картин (рис. 294). На картине проведем диагональ и найдем ее середину, которая одновременно является центром окружности, описанной вокруг этой кар-

Рис. 294 208

тины. Из середины диагонали построим перпендикуляр, равный по вели­чине дистанционному расстоянию, определим новое положение совмещен­ной точки зрения S_k. Прямые, соединяющие концы диагонали с точкой S_k, образуют при ней угол ясного зрения.

На рис. 294,а диаметр поля ясного зрения равен диагонали картины. Это возможно только тогда, когда линия горизонта проходит по середине картины, а главная точка совпадает с ее геометрическим центром, что встре­чается редко. Если дистанционное расстояние равно диагонали, то угол зрения равен 53°. Если дистанционное расстояние в полтора раза больше диагонали, то угол равен 37° (рис. 294,6). При длине серединного перпен­дикуляра, равной двум диагоналям картины, угол зрения составит 28° (рис. 294,в).

Рис. 295 14 Э-298 209

На схеме с картины Б.М. Кустодиева «Торговка овощами» (рис. 295) на переднем плане изображены под произвольным углом к зрителю ящики с помидорами и картофелем. Итак, на картинной плоскости имеются два пря­мых угла с различным направлением сторон. Этого достаточно для нахож­дения основных элементов картины. Определим точки схода сторон каж­дого прямого угла F_lt F₂ и F₃, F_A и линию горизонта. При каждой паре точек схода проведем полуокружности. Точка пересечения полуокружностей — совмещенная точка зрения S_k, а перпендикуляр, опущенный на линию го-

ризонта определит главную точку картины Р. Зная положение дистанци­онных точек Z>! и D₂, найдем угол ясного зрения. Расстояние PS_k больше диагонали картины, значит угол составит 50°.

Если задан интерьер комнаты с фронтальной стеной, то легко опреде­лить по направлению плинтусов и карнизов главную точку картины и ли­нию горизонта. Если в такой комнате имеется полуоткрытая дверь или окно, то совмещенную точку зрения, а затем и дистанционное расстояние опре­делим с помощью масштабной точки, как это показано на схеме с картины неизвестного русского художника «Биллиардная в Пущине, имении Стре-каловых» (рис. 296). Верхний и нижний края двери продолжим до пересе­чения с линией горизонта и получим точку схода F_x. Так как в натуре ши­рина двери и ее проема равны, то проведя линию переноса через угол по­лотна двери А и соответствующий угол А₁ в проеме, получим на линии горизонта масштабную точку М_х для произвольно направленной прямой, имеющую точку схода F_x. Масштабная точка определяется равенством рас­стояний F₁S_k= F^M^ Поэтому проведя дугу радиусом F_xM_r до пересечения с перпендикуляром, проведенным через точку Р к линии горизонта, полу­чим совмещенную точку зрения S_k. Отложив отрезок PS_k = PD, найдем ди­станционные точки D₁ и D₂. Угол ясного зрения превысит 60°, что бесспор­но отрицательно влияет на зрительное восприятие картины.

Рис. 296 210

Восстановление основных элементов картины и определение размеров предметов по их перспективному изображению называют реконструкци­ей. Однако во многих случаях перспективный анализ картин можно сде-

лать приблизительно. Следует учесть, что иногда художник прибегает к умышленному нарушению законов перспективных построений и применяет несколько линий горизонта и главных точек.

При восстановлении элементов картины нужно уметь определять ее масштаб и натуральные размеры изображаемых предметов. Это можно сде­лать разными способами. Если требуется найти натуральную величину от­дельного предмета безотносительно к другим, то проще это делать через перспективные масштабы, как показано на схеме с картины Жака Луи Да­вида «Клятва Горациев» (рис. 297). Натуральную величину аркады в мас­штабе картины найдем, используя перспективный масштаб.

Если сюжет картины связан с интерьером, в котором находятся фигура человека и предметы обстановки, то по их размерам можно определить вы­соту линии горизонта и натуральную единицу масштаба картины. Рост взрослого человека составляет 1,6—1,8 м. Эти данные дают возможность определить масштаб картины и размеры отдельных предметов. В картине Ж.Л. Давида линия горизонта совпадает с уровнем глаз стоящего челове­ка, значит высота ее примерно 1,70 м, а величина арки — 2,50 м.

Рис. 297

На схеме картины Алексея Гавриловича Венецианова «Утро помещи­цы» основные элементы найдены по-другому (рис. 298). Картина, написан-

ная масляными красками, невелика по размеру и выполнена в бытовом жанре. Однако в картине нет сюжетной завязки, показанное действие од­носложно. Спокойные лица, некоторая застылость поз придает этой карти­не характер не столько жанровой сцены, сколько эпизода привычного те­кущего бытия, на минуту остановленного художником.

Эффект спокойствия и равновесия во многом определяется и выбран­ным уровнем горизонта. Продолжив половицы пола до их пересечения, найдем главную точку картины. Линия горизонта располагается на уровне глаз главной героини, которая сидит в кресле. Значит, примерно составля­ет 1,20 м. Эту же величину получим, используя высоту стола, изображен­ного в комнате. Для этого его величину вынесем в плоскость картины с по­мощью масштаба высот. В масштабе картины натуральный размер стола будет 0,75 м. Расстояние от крышки стола до линии горизонта составляет ¹/₂ высоты стола примерно 37—40 см (0,75 + 0,40). Определим высоту шир­мы, расположенной в глубине картины. Она составляет 1,90 м.

Вынос главной точки картины за ее пределы уменьшает глубину про­странства, значительно приближает сцену к зрителю и как бы делает его соучастником происходящего. Основное изобразительное средство худож­ника в этом произведении — свет, которым он выделяет главных действу-

а = 75°

 

Рис. 298 212

ющих лиц, все остальные предметы погружены в прозрачную тень. Глав­ная точка картины фактически совпадает с источником света (окно сверху прикрыто портьерой). Эта работа наилучшим образом демонстрирует дос­тижения, которые были сделаны мастером в области нового понимания интерьера для реальной передачи сцен повседневной жизни.

Рис. 299

Картина П.А. Федотова «Завтрак аристократа» выполнена также в бы­товом жанре (рис. 299). Художник дает повествовательное раскрытие со­бытия, с едкой иронией представляет на первом плане главного персона­жа, который пытается прикрыть кусок черного хлеба. Для выявления го-

ловы центральной фигуры используются линии стола, уходящие в глуби­ну и позволяющие определить главную точку картины и линию горизонта. Диагональ квадрата на ковре позволяет сразу определить дистанционное расстояние, и совмещенную точку зрения.

Проще всего произвести реконструкцию стула, так как он максимально приближен к основанию картины и имеет вполне определенные размеры — величина от пола до сиденья составляет 0,45 м, у стола — высота 0,75 м. Оп­ределим высоту линии горизонта — 1,20 м и высоту комнаты — 3,75 м.

Точка зрения удалена на расстояние меньше диагонали картины, зна­чит художник писал картину, как бы наблюдая сцену через окно, откуда падает свет на фигуру. Близкая к картине точка зрения вызвала подчерк­нутые перспективные явления — крутой сход глубинных прямых в глав­ную точку картины. Создается впечатление, что пол поднимается к даль­ней стене комнаты. Однако при общем восприятии картины эти искаже­ния не очень заметны.

Поскольку задана фронтальная перспектива интерьера для определе­ния взаимного положения предметов обстановки, воспользуемся методом гомологии, изложенным ранее. Из совмещенной точки зрения S_k проведем лучи зрения через дальние углы комнаты, и получим ее план. Ковер, в ос­нове рисунка которого лежат квадраты, позволяет достаточно точно опре­делить местоположение кресла и шкафов.

Приведенные примеры далеко не исчерпывают все возможные случаи использования художниками перспективных построений для решения ком­позиционных задач, однако они дают общее представление о закономерно­стях передачи трехмерных изображений на плоскости листа.

Вопросы и упражнения для самоконтроля

1. Приведите примеры картин художников, где изображены отражения в воде или зеркалах.

2. На каких законах оптики основано построение отражений в перспективе?

3. В чем заключается сущность построения отражений предмета в плоском зер­кале?

Глава IX

ФОРМИРОВАНИЕ И РАЗВИТИЕ

ПЕРСПЕКТИВЫ КАК НАУКИ

В глубокой древности, на самых ранних этапах развития человеческо­го общества, человек изображал на двумерных поверхностях (стены пеще­ры, плоские кости и дерево) животных и различные предметы, которые ок­ружали его. Рисунки имели магическое, информационное и декоративное значения.

Древнеегипетское искусство во многом близко детскому рисунку, по­этому его иногда называют наивным. Человек еще не умел передать про­странство на плоскости, он стремился «распластать» объемные тела.

Возможность сделать следующий шаг в совершенствовании методов изображения пространственных фигур дала Античность. Поскольку гре­ческая живопись не сохранилась, мы можем судить о ней только по древ­ним литературным источникам.

Высокое развитие скульптуры свидетельствует, что стремление древ­негреческих художников к правдивому изображению сильного, энергич­ного, отличающегося душевным равновесием человека требовало приме­нения теоретических знаний изображения реальной формы, которые дол­жны были отвечать законам зрительного восприятия. Во многом этому способствовало высокое развитие аксонометрии и математики в целом. Древнегреческий ученый Эсхил (около 525 — 456 гг. до н. э.) внес значи­тельный для того времени вклад в развитие наблюдательной перспективы. Большое внимание построениям изображений на плоскости уделено в трак­тате «О геометрии» крупнейшего ученого, естествоиспытателя и мыслите­ля Древней Греции Демокрита (около 460—370 гг. до н. э.).

Способы построения перспективных изображений изложил в трактате «Десять книг об архитектуре» древнегреческий ученый и архитектор Вит-рувий (конец I в. до н. э.), где без теоретических обоснований сформулиро­вал правила построения перспективных изображений и составления архи-

Рис. 300. План купола с перспективной передачей конструкции, выполненный Филиппо Брунеллески

тектурно-строительных чертежей планов и фасадов зданий. Эти трактаты использовали римские художники. В помпеиских росписях появилась ось схода — «рыбья кость» — своеобразная предшественница точки схода в ренессансной системе перспективы.

В течение длительного времени (около тысячи лет) наука о построении графических изображений не получила дальнейшего развития. Для Сред­невековья характерно стремление к отвлеченному, мистическому, незем­ному искусству. Материально-чувственные изображения людей в произве­дениях греческих мастеров, воспевавших красоту тела, считались непри­емлемыми. В иконописи широко использовалась обратная перспектива, когда дальние объекты изображались более крупными, чем ближние.

Эпоха Возрождения впервые создала математически строгое учение о способах передачи пространства, назвав его линейной перспективой. Счи­тают, что перспектива как наука возникла в Италии в XV в. Открытие за­кономерностей в перспективе стало большим событием в области изобрази­тельного искусства. Наука о перспективе внесла в произведения художни­ков логический порядок и композиционную целостность.

Основоположником перспективы как науки считают итальянского те­оретика искусства, архитектора и художника эпохи Возрождения Филип­по Брунеллески (1377—1446), который впервые стал применять правила перспективы в изображении архитектурных сооружений (рис. 300).

Итальянский ученый Леон Баттиста Альберти (1404—1472) — теоретик искусства Раннего Возрождения, одаренный математик, физик, замечатель­ный зодчий, скульптор, философ, поэт и музыкант — обобщил опыт мастеров античного и современного ему изобразительного искусства. Теоретические положения о перспективе на математической основе изложены в его трудах «О живописи» и «О зодчестве». В трактате «Десять книг о зодчестве» он сфор­мулировал на научной основе теорию рисунка и перспективы, обосновал тео­рию пропорций по принципу греческой антропометрии¹.

Альберти предлагал строить процесс обучения на рисовании с натуры, где можно наблюдать изменения в размерах и измерять их. Для построения пер­спективных изображений он использовал способ перспективной сетки. Аль­берти применил масштабные точки, в которые сходятся диагонали квадра­тов. Правда, он не дал этому свойству теоретических обоснований, так как считал данные построения естественными и понятными с первого взгляда. Альберти также рассмотрел теорию нанесения теней на изображениях и обо­сновал необходимость покрытия освещенных поверхностей разными тонами красок, т.е. ввел впервые понятие светотени.

Теоретическое наследие Пьеро делла Франческа (около 1420—1492) от­ражает достижения флорентийской школы живописи. Он дал определение перспективы как проекции предмета, полученное в результате пересечения конуса видимости с картинной плоскостью в своих трактатах «О правильных телах» и «О живописной перспективе». В своем искусстве он соединил совер­шенную перспективу и строгую пропорциональность форм с тонкой гармони­ей красок. Художники того времени считали его отцом линейной перспекти­вы. Сохранились подготовительные рисунки к некоторым его работам, на которых видны линии построения и сильное сокращение боковой стены дома.

Леонардо да Винчи (1452—1519) соединил в себе черты эксперимента­тора и взыскательного теоретика, требующего самых обоснованных мето­дов доказательств. Свои теоретические положения, в том числе правила перспективы, он изложил в трактате «О живописи». Леонардо да Винчи считал, что перспектива относится к «механическим наукам», которыми не должен пренебрегать ни один талантливый живописец. Он подчеркивал большое значение перспективы как науки в развитии живописи и указы­вал, что практика всегда должна быть построена на хорошей теории, для которой перспектива является руководителем и без нее ничто не может быть сделано хорошо в живописи.

Леонардо да Винчи делит перспективу на три основные части:

1. Линейная перспектива, изучает и излагает законы построения фи­гур по мере их удаления от наблюдателя.

2. Воздушная и цветовая перспектива, трактует об изменении цвета предметов в зависимости от расстояния от них до наблюдателя и о влиянии слоя воздуха на насыщенность и локальность цвета.

¹ Антропометрия (греч.) — наука о методах измерения человеческого тела.

3. Перспектива четкости очертания формы предметов анализирует из­менение степени отчетливости границ фигур и контраста света и тени по мере удаления их в глубину пространства, изображаемого на картине.

Из трех разделов перспективы два последних не получили дальнейшего теоретического развития. Из-за сложности исследования цветовая и воздуш­ная перспективы не имели аргументированных законов, поэтому художни­ки используют их на практике на основе личного восприятия и опыта.

В художественном и научном наследии великого мастера сохранилось много рисунков и набросков, где изображения выполнены с использованием перспективных сокращений. Леонардо да Винчи предлагал строить улицы на разных уровнях с целью беспрепятственного движения на перекрестках.

Выдающийся немецкий ученый, математик, гравёр и художник, Аль­брехт Дюрер (1471—1528) в своем сочинении «Руководство для измерения циркулем и правилом», изданном в 1523 г., описал графический способ построения перспективы предметов с использованием ортогональных про­екций, получивший в литературе название «способ Дюрера». Дюрер изоб­рел приспособление для измерения пропорций фигуры человека. На одной из гравюр А. Дюрера изображен художник, рисующий музыкальный ин­струмент — лютню (рис. 301). Он смотрит на лютню одним глазом, сквозь очко и через раму с сеткой из квадратных ячеек. Рама с сеткой удалена от очка настолько, чтобы и раму, и лютню можно было увидеть целиком, не поворачивая головы, т. е. не перемещая точки зрения. На столе перед ху­дожником лежит лист бумаги с такой же сеткой из квадратов, на который мастер и переносит образ, увиденный через очко.

Рис. 301. Гравюра Альбрехта Дюрера

Хорошо зная математику, Дюрер предлагал фигуру человека вписывать в простейшую геометрическую форму, которую легко проверить законами перспективы, а затем детализировать мелкие части. Рисовальщик вначале

должен видеть большую форму, а затем подобно скульптору рубить ее с выявлением объемно-конструктивного строения. Большую ценность для рисования представляет учение Дюрера о фигурах и возникший на его ос­нове так называемый «метод обобщения формы».

Геометрическая точность построения никогда не была самоцелью для художников-реалистов. Для них перспектива была лишь одним из средств художественной выразительности. Законы перспективы не сковывали их творческую инициативу, а позволяли при осмотрительном использовании их находить более сложные закономерности.

Анализ картин выдающихся художников Возрождения показывает, что отступление от сложившихся упрощенных геометрических принципов было не отрицанием математической логики, а было интуитивной коррек­тировкой в сторону визуальной правильности передачи пространства. На­личие нескольких линий горизонта или точек схода для линий, идущих в глубину — эти отступления можно видеть в картинах Веронезе, Рафаэля, Леонардо да Винчи.

Итальянский ученый, архитектор и художник Андреа дель Поццо (1642—1709), описал теорию перспективы в работе «Перспектива архитек­торов и живописцев, в которой излагается легчайший и быстрейший спо­соб перспективного изображения всего, что относится к архитектуре» (Рим, 1693 г.). Название книги вполне оправдано, в ней приведены многочислен­ные и оригинальные примеры построения перспективных изображений по ортогональным чертежам (рис. 302, а, б). В этом же труде были даны, до­вольно полные для того времени, сведения о различных видах перспекти­вы: линейной, рельефной и плафонной.

К концу XVIII в. была решена задача передачи переднего, среднего и дальнего планов (до горизонта, если это было необходимо), что чрезвычай­но расширило возможности художников.

Однако перспективные изображения, несмотря на их наглядность, не дают полного представления о форме и размерах изображаемого предмета, они не могут быть использованы как проекты для осуществления каких-либо сооружений. Начало XIX в. ознаменовалось новыми открытиями в науке о методах изображения. Знаменитый французский ученый, геометр и инже­нер, общественный деятель эпохи Великой Французской революции Гаспар Монж (1746—1818) опубликовал в 1795 г. свою книгу «Начертательная гео­метрия», которая явилась первым систематизированным изложением мето­да изображения пространственных фигур на плоскости. В этой книге впервые были сделаны попытки построить тени на ортогональном чертеже — эпюре и в перспективе. В ней изложены рекомендации, как выполнить тушевку пред­мета в соответствии с законами воздушной перспективы. Работы Гаспара Монжа явились своеобразным логическим завершением всего, что было сде­лано раньше, и началом нового этапа в развитии науки о построении графи­ческих изображений — начертательной геометрии.

а)

б)

Рис. 302. Рисунки из книги Андреа дель Поццо «Перспектива архитекторов

и живописцев, в которой излагается легчайший и быстрейший способ

перспективного изображения всего, что относится к архитектуре»

Первые сведения о перспективных изображениях в России относятся к концу XV в. и связаны со строительством соборов Московского Кремля. Итальянские архитекторы привезли в Россию перспективы храмов и собо­ров, однако на изобразительное искусство той эпохи они не повлияли в свя­зи с сильными национальными художественными традициями. Долгое вре­мя перспективу использовали только для изображения архитектурных и технических сооружений.

Русские художники XVI—XVII вв. уже достаточно хорошо овладели теорией перспективы и применяли ее в своих картинах с большим мастер­ством. Это подготовило следующий этап в развитии теории и практики пер­спективы, который внесли русские художники-педагоги XVIII—XIX вв.

В 1822 г. Василий Козьмич Шебуев (1777—1855), воспитавший целую плеяду замечательных художников, написал трактат из четырех частей «Полный курс правил рисования и анатомии для воспитанников Академии художеств». Этот труд, в двух частях которого отводилось место перспек­тиве, представлял собой строгую систему правил рисования фигуры чело­века и его частей тела, и содержал 150 учебно-методических рисунков-ил­люстраций и методические советы по рисованию с натуры и применению знаний законов перспективы и пластической анатомии в академическом

рисунке.

Значительный вклад в систему художественного образования внесли рус­ские художники-педагоги XIX в. Алексей Гаврилович Венецианов (1780— 1847) посвятил 20 лет жизни напряженным поискам закономерностей видения натуры на основе законов перспективы. Картины А.Г. Венецианова — лучшие иллюстрации к его теоретическим высказываниям. Большое значение имело учебно-методическое пособие А.П. Сапожникова «Полный курс рисования», изданного в 1834 году, который неоднократно переиздавался и изучался многи­ми поколениями художников. Замечательный русский художник и педагог Николай Николаевич Ге (1831—1894) рекомендовал своим ученикам сделать перспективу всегдашним спутником своей работы, учить, овладевать и вносить в каждое произведение. Каждая картина П. А. Федотова, Н.Н. Ге, А.Г. Венеци­анова и других художников может рассматриваться как учебное пособие к кур­су перспективы, по которому можно изучать применение перспективных пост­роений для реализации композиционного замысла.

Выдающийся художник-педагог Павел Петрович Чистяков (1832—1919) считал, что форма предмета в пространстве не может быть нарисована с homoj щью «талантливого глаза», она требует строго точной проверки, основанной на самых точных правилах, т. е. перспективе. Большим событием во второй половине XIX в. в России было введение в общеобразовательной школе учеб­ных предметов по рисованию и черчению. В разработке программ по этим дисциплинам принимал участие и П.П. Чистяков. Система Чистякова полу­чила широкое признание, у него учились почти все крупные художники-реа­листы той эпохи, составившие славу русской школы.

В различных сферах человеческой деятельности к изображению объек­тов предъявляются неодинаковые требования. В изобразительном искус­стве усилия художников направлены на изображение с наибольшей степе­нью наглядности. В технике важны расчетные характеристики, наглядно­сти не придается столь серьезного значения. Для технических целей необходимы изображения, которые дают наиболее полную информацию о размерах объекта. Поэтому не случайно на протяжении всего XIX в. на­блюдается параллельное развитие и изучение методов отображения окру­жающего мира в разных сферах деятельности. Метод ортогонального про­ецирования изучается в начертательной геометрии, которая становится самостоятельной наукой и вводится как обязательный предмет в высших технических учебных заведениях. Раздел перспективы изучается как спе­циальный предмет в художественных учебных заведениях.

Первым русским профессором по начертательной геометрии, ее осно­воположником и основателем этой науки в России был Яков Александро­вич Севастьянов (1796—1849). Изданной им в 1821 г. учебник «Основания начертательной геометрии» стал первым учебником русского автора на рус­ском языке и явился основным в течение 20 лет почти во всех высших учеб­ных заведениях. Я.А. Севастьянов впервые ввел русскую терминологию, дал практическое приложение начертательной геометрии к техническому черчению, рисованию, перспективе и картографии. А.Я. Севастьянов на­писал ряд работ, среди которых наиболее известные: «Приложение начер­тательной геометрии к рисованию. Теория теней. Линейная перспектива. Оптические изображения», «Приложение начертательной геометрии к воз­душной перспективе, к проекции карт и к гномонике».

Рубеж XIX—XX вв. ознаменовался новым подъемом в изобразитель­ном искусстве. Появление картин, выполненных по законам «перцептив­ной» перспективы, с учетом кривизны прямых линий в среднем простран­стве, свидетельствует о значительном продвижении человеческой мысли в процессе познания себя и окружающего мира. Творчество французкого ху­дожника П. Сезана (1839—1906) и русского художника К.С. Петрова-Вод-кина (1878—1939) — лучшее тому подтверждение.

Крупнейшим теоретиком перспективы XX в. стал Борис Викторович Раушенбах (1915—2001), выдающийся ученый-математик, один из созда­телей отечественной ракетно-космической техники, философ, мыслитель, автор работ, посвященных богословским и искусствоведческим проблемам, где исследует вопросы зрительного восприятия человека, роли мозга и воз­можностей отражения трехмерного пространства на плоскости картины.

К началу XXI в. был накоплен огромный практический опыт, вопло­щенный многими поколениями художников в различных произведениях искусств; перспектива как наука определила свои закономерности, прави­ла и исключения.