Цель работы: Написать программу для минимизации функции одной переменной методом золотого сечения и функции двух переменных методами Хука–Дживса и градиентного спуска.
Теоретические основы
Одномерная минимизация
Метод золотого сечения
Одним из наиболее эффективных методов, в которых при ограниченном количестве вычислений f(x) достигается наилучшая точность, является метод золотого сечения. Он состоит в построении последовательности отрезков [ а 0, b 0], [ а 1, b 1], …, стягивающихся к точке пересечения графика функции f(x) с осью x. На каждом шаге, за исключением первого, вычисление значения функции f(x) проводится лишь один раз. Эта точка, называемая золотым сечением, выбирается специальным образом.
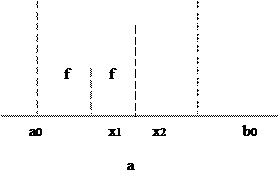
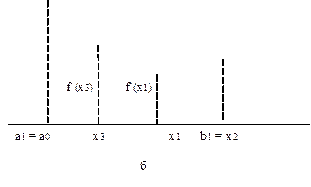
Рисунок 2 – Метод золотого сечения
Поясним сначала идею метода геометрически, а затем выведем необходимые соотношения. На первом шаге процесса внутри отрезка [ а 0, b 0] (рис. 2а) выбираем две внутренние точки х 1и х 2и вычисляем значения целевой функции f(x 1 ) и f(x 2 ). Поскольку в данном случае 
, очевидно, что решение расположено на одном из прилегающих к x 1 отрезков [ а 0, x 1] пли [ x 1, x 2]. Поэтому отрезок [ x 2, b 0] можно отбросить, сузив тем самым первоначальный интервал неопределенности.
Второй шаг проводим на отрезке [ а 1, b 1] (рис. 2б), где а 1 = а 0, b 1= х 2. Нужно снова выбрать две внутренние точки, но одна из них (x 1) осталась из предыдущего шага, поэтому достаточно выбрать лишь одну точку х 3, вычислить значение f(х 3 ) и провести сравнение. Поскольку здесь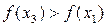 
, ясно, что решение находится на отрезке [ х 3, b 1].Обозначим этот отрезок [ а 2, b 2], снова выберем одну внутреннюю точку и повторим процедуру сужения интервала неопределенности. Процесс повторяется до тех пор, пока длина очередного отрезка [ аn, bn ] не станет меньше заданной величины 
.
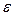Теперь рассмотрим способ размещения внутренних точек на каждом отрезке [ аk, bk ].Пусть длина интервала неопределенности равна l, а точка деления делит его на части l 1, l 2: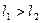 
. Золотое сечение интервала неопределенности выбирается так, чтобы отношение длины большего отрезка к длине всего интервала равнялось отношению длины меньшего отрезка к длине большего отрезка:
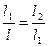
Из этого соотношения можно найти точку деления, определив отношение 
:
Поскольку нас интересует только положительное решение, то
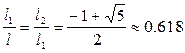
Отсюда: 
Поскольку заранее неизвестно, в какой последовательности (l 1и l 2 или l 2 и l 1)делить интервал неопределенности, то рассматриваются внутренние точки, соответствующие двум этим способам деления.
На рис. 3 а точки деления x 1, x 2выбираются с учетом полученных значений для частей отрезка. В данном случае имеем:
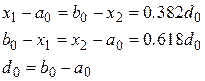
После первого шага оптимизации получается новый интервал неопределенности – отрезок [ а 1, b 1](рис. 2). Точка x 1делит этот отрезок в требуемом отношении, при этом
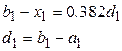
Вторая точка деления х3 выбирается на таком же расстоянии от левой границы отрезка, т. е.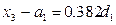 
. И снова интервал неопределенности уменьшается до размера:
Тогда координаты точек деления у и z отрезка.[ ak, bk ]на k+ 1–м шаге оптимизации (у < z):
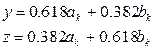
При этом длина интервала неопределенности равна:
Процесс заканчивается при выполнении условия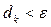 
.
Многомерная минимизация
Метод градиентного спуска
Общая задача нелинейного программирования без ограничений состоит в минимизации функции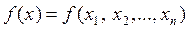 
, заданной во всем n –мерном евклидовом пространстве. Функция 
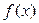называется целевой функцией.
Как правило, численные методы нахождения экстремума состоят в построении последовательности векторов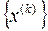 
, удовлетворяющих условию: 
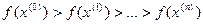. Методы построения таких последовательностей называются методами спуска. В этих методах элементы последовательности 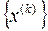вычисляются по формуле:
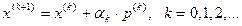
где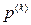 
– направление спуска; 
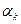– длина шага в этом направлении.
Как известно, градиент функции в некоторой точке 
направлен в сторону наискорейшего локального возрастания функции. Следовательно, спускаться нужно в направлении, противоположном градиенту. Вектор, противоположный градиенту, называется антиградиентом. Выбирая антиградиент в качестве направления спуска, приходят к итерационному процессу вида:
, (2)
где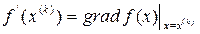 
Все методы спуска, в которых вектор 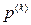совпадает с антиградиентом, называются градиентными методами. Они отличаются друг от друга только способом выбора шага. Наиболее употребительны метод наискорейшего спуска и метод дробления шага.
В методе наискорейшего спуска величина 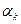определяется из условия
,
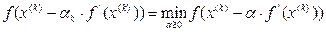т.е. на каждом шаге решается одномерная задача минимизации. Геометрическая интерпретация этого метода достаточно проста (рис. 3). Заметим, что на двух последовательных шагах направления спуска ортогональны.
Если 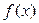– ограниченная снизу, непрерывно дифференцируемая функция и для некоторой начальной точки 
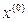множество 
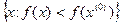также ограничено, то для метода наискорейшего спуска последовательность 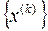либо сходится к точке минимума при 
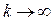, либо достигает точки минимума за конечное число шагов.
Процесс (2) с дроблением шага протекает следующим образом. Выбираем некоторое начальное значение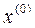 
. Общих правил выбора 
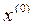нет: если есть информация о расположении точки минимума, то точку 
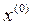выбираем в этой области. Затем выбираем некоторое 
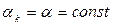и на каждом шаге процесса (2) проверяем условие монотонности 
. Если это условие нарушается, то 
дробим до тех пор, пока монотонность не восстановится. Для окончания счета используем критерий:
В этом случае полагаем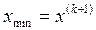 
.
Здесь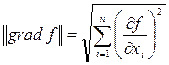 
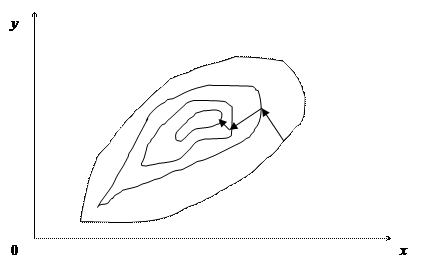
Рисунок 3 – Метод градиентного спуска
Метод Хука–Дживса
Процедура Хука–Дживса представляет собой комбинацию исследующего поиска с циклическим изменением переменных и ускоряющего поиска по образцу.
Исследующий поиск. Для проведения исследующего поиска необходимо знать величину шага, которая может быть различной для разных координатных направлений и изменяться в процессе поиска. Исследующий поиск начинается в некоторой исходной точке. Если значение целевой функции в пробной точке не превышает значение в исходной точке, то шаг поиска рассматривается как успешный. В противном случае надо вернуться в предыдущую точку и сделать шаг в противоположном направлении с последующей проверкой значения целевой функции. После перебора всех n– координат исследующий поиск завершается. Полученную в результате точку называют базовой точкой.
Поиск по образцу. Поиск по образцу заключается в реализации единственного шага из полученной базовой точки вдоль прямой, соединяющей эту точку с предыдущей базовой точкой. Новая точка образца определяется в соответствии с формулой:
Как только движение по образцу не приводит к уменьшению целевой функции, точка 
фиксируется в качестве временной базовой точки и вновь проводится исследующий поиск. Если в результате получается точка с меньшим значением целевой функции, чем в точке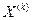 
, то она рассматривается как новая базовая точка 
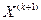. С другой стороны, если исследующий поиск неудачен, необходимо вернуться в точку 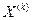и провести исследующий поиск с целью выявления нового направления минимизации. В конечном итоге возникает ситуация, когда такой поиск не приводит к успеху. В этом случае требуется уменьшить величину шага путем введения некоторого множителя и возобновить исследующий поиск. Поиск завершается, когда величина шага становится достаточно малой. Последовательность точек, получаемую в процессе реализации метода, можно записать в следующем виде:
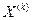– текущая базовая точка,
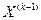– предыдущая базовая точка,
– точка, построенная при движении по образцу,
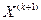– следующая (новая) базовая точка.
Приведенная последовательность характеризует логическую структуру поиска по методу Хука–Дживса.
Алгоритм метода:
1. Выбрать начальную базисную точку b 1 и шаг длиной h 1 для каждой переменной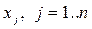 
2. Вычислить f (х) в базисной точке b 1 с целью получения сведений о локальном поведении функции f (х). Эти сведения будут использоваться для нахождения подходящего направления поиска по образцу, с помощью которого можно надеяться достичь большего убывания значения функции. Функция f (х) в базисной точке b 1, находится следующим образом:
а) Вычисляется значение функции f (b 1) в базисной точке b 1.
б) Каждая переменная по очереди изменяется прибавлением длины шага. Таким образом, мы вычисляем значение функции 
, где 
единичный вектор в направлении оси x 1. Если это приводит к уменьшению значения функции, то b 1 заменяется на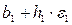 
. В противном случае вычисляется значение функции 
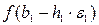, и если ее значение уменьшилось, то b 1 заменяем на 
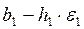. Если ни один из проделанных шагов не приводит к уменьшению значения функции, то точка b 1 остается неизменной и рассматриваются изменения в направлении оси х 2, т. е. находится значение функции 
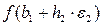и т. д. Когда будут рассмотрены все n переменных, мы будем иметь новую базисную точку b 2.
в) Если 
, т. е. уменьшение функции не было достигнуто, то исследование повторяется вокруг той же базисной точки b 1, но с уменьшенной длиной шага. На практике удовлетворительным является уменьшение шага (шагов) в десять раз от начальной длины.
г) Если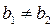 
, то производится поиск по образцу.
3. При поиске по образцу используется информация, полученная в процессе исследования, и минимизация функции завершается поиском в направлении, заданном образцом. Эта процедура производится следующим образом:
а) Разумно двигаться из базисной точки b 2 в направлении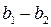 
, поскольку поиск в этом направлении уже привел к уменьшению значения функции. Поэтому вычислим функцию в точке образца:
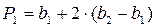
В общем случае:
б) Затем исследование следует продолжать вокруг точки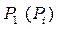 
.
в) Если наименьшее значение на шаге 3б) меньше значения в базисной точке b 2 (в общем случае bi +1), то получают новую базисную точку b 3 (bi +2), после чего следует повторить шаг 3а). В противном случае, не производить поиск по образцу из точки b 2 (bi +1), а продолжить исследования в точке b 2 (bi +1).
4. Завершить этот процесс, когда длина шага (длины шагов) будет уменьшена до заданного малого значения.
Задание
1. Написать программу для минимизации функции ¦ (x) методом золотого сечения;
2. Написать программу для минимизации функции ¦ (x1, х2) методами Хука–Дживса и градиентного спуска.
Контрольные вопросы
