Цель работы: освоить навыки нахождения значения полинома различными методами, с оценкой точности произведенных вычислений и количества производимых математических действий
Теоретические основы
При аппроксимации функций, а также в некоторых других задачах приходится вычислять значения полиномов вида
Q(p) = a 0 pn + a 1 pn –1+ a 2 pn –2+…+ an –1 p + an
Если проводить вычисления «в лоб», т.е. находить значения каждого члена и суммировать их, то при больших п потребуется выполнить большое число операций (n 2+ n/ 2умножений и п сложений). Кроме того, это может привести к потере точности за счет погрешностей округления. В некоторых частных случаях, как это сделано при вычислении синуса, удается выразить каждый последующий член через предыдущий и таким образом значительно сократить объем вычислений.
Метод Горнера
Анализ многочлена в общем случае приводит к тому, что для исключения возведения х в степень в каждом слагаемом полином целесообразно переписать в виде:
p(a 0 pn –1+ a 1 pn –2+ a 2 pn –3+…+ an –1 ) + an,
в следующей итерации он принимает вид:
p(p(a 0 pn –2+ a 1 pn –3+ a 2 pn –4+…+ an –2 ) + an –1 ) + an.
Прием, с помощью которого полином представляется в таком виде, называется схемой Горнера. Этот метод требует п умножений и п сложений. Использование схемы Горнера для вычисления значений полиномов не только экономит машинное время, но и повышает точность вычислений за счет уменьшения погрешностей округления.
1) вычисление значения полинома последовательным перемножением:


n n –1 n –2
2) вычисление методом Горнера

3) вычисление значения полинома возведением в степень оператором «^»

4) вычисления значения полинома возведением в степень с использованием формулы 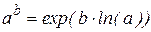
Задание
Написать программу нахождения значения полинома n –ой степени четырьмя методами, в качестве значения p задавать дробные.
Контрольные вопросы
Лабораторная работа №5 ВЫЧИСЛЕНИЕ ОПРЕДЕЛИТЕЛЯ МАТРИЦЫ ПРИВЕДЕНИЕМ К ТРЕУГОЛЬНОМУ ВИДУ
Цель работы: написать программу для нахождения определителя матрицы размерностью n×n
Теоретические основы
Среди задач линейной алгебры существуют такие задачи как вычисление определителей нахождение обратных матриц, собственных значений матрицы и др. Легко вычисляются лишь определители невысоких порядков и некоторые специальные типы определителей.
В частности, для определителей второго и третьего порядков соответственно имеем:
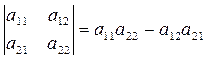
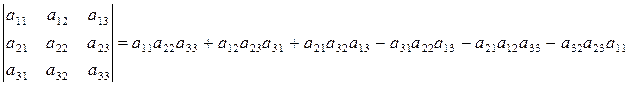
Определитель треугольной матрицы равен произведению ее элементов, расположенных на главной диагонали: 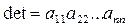 .Треугольной называется матрица, у которой все элементы находящиеся ниже главной диагонали имеют нулевое значение.
.Треугольной называется матрица, у которой все элементы находящиеся ниже главной диагонали имеют нулевое значение.
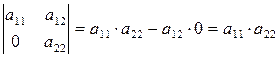
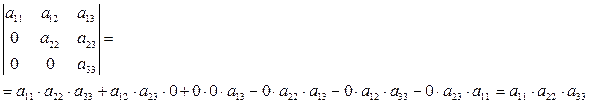
Отсюда также следует, что определитель единичной матрицы равен единице, а нулевой – нулю:  .
.
В общем случае вычисление определителя оказывается значительно более трудоемким. Определитель D порядка п имеет вид:
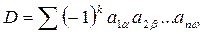
Из этого выражения следует, что определитель равен сумме п!слагаемых, каждое из которых является произведением п элементов. Поэтому для вычисления определителя порядка п (без использования специальных приемов) требуется 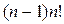 умножений и
умножений и 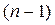 сложений, т. е. общее число арифметических операций равно
сложений, т. е. общее число арифметических операций равно

Оценим значения N в зависимости от порядка п определителя:
| п | |||
| N | 3.6 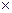 107 107
| 5  1019 1019
|
Итак, непосредственное нахождение определителя требует большого объема вычислений. Вместе с тем легко вычисляется определитель треугольной матрицы: он равен произведению ее диагональных элементов.
Для приведения матрицы к треугольному виду может быть использован метод исключения, т. е. прямой ход метода Гаусса. В процессе исключения элементов величина определителя не меняется. Знак определителя меняется на противоположный при перестановке его столбцов или строк. Следовательно, значение определителя после приведения матрицы А к треугольному виду вычисляется по формуле:

Здесь диагональные элементы 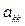 берутся из преобразованной (а не исходной) матрицы. Знак зависит от того, четной или нечетной была суммарная перестановка строк (или столбцов) матрицы при ее приведении к треугольному виду (для получения ненулевого или максимального по модулю ведущего элемента на каждом этапе исключения). Благодаря методу исключения можно вычислять определители больших порядков, при значительно меньшем объеме вычислений, чем в проведенных ранее оценках.
берутся из преобразованной (а не исходной) матрицы. Знак зависит от того, четной или нечетной была суммарная перестановка строк (или столбцов) матрицы при ее приведении к треугольному виду (для получения ненулевого или максимального по модулю ведущего элемента на каждом этапе исключения). Благодаря методу исключения можно вычислять определители больших порядков, при значительно меньшем объеме вычислений, чем в проведенных ранее оценках.
Приведение к треугольному виду достигается последовательным исключением элементов в нижних строках матрицы. Сначала с помощью первой строки исключается первый элемент всех строк. Затем с помощью второй строки исключается второй элемент третьей и всех последующих строк. Этот процесс, продолжается до тех пор, пока в последней (п– ой ) строке не останется лишь один элемент.
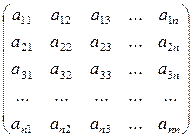
1–ый шаг:

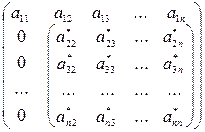
n –ый шаг 

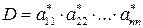
Задание
Написать программу для нахождения определителя матрицы размерностью n×n.
Контрольные вопросы






