Федеральное агенство по образованию
Государственное образовательное учреждение
Высшего профессионального образования
КАМСКАЯ ГОСУДАРСТВЕННАЯ ИНЖЕНЕРНО–ЭКОНОМИЧЕСКАЯ АКАДЕМИЯ
Лабораторный практикум
По дисциплине
"Программирование и основы алгоритмизации"
Для студентов очного и заочного отделений по специальности
"Автоматизация технологических процессов и производств"
УДК
Лабораторный практикум по дисциплине "Программирование и основы алгоритмизации" для студентов специальности 2102 "Автоматизация технологических процессов и производств". /Валиахметов Р.Р., Гумеров А.Ф., Зубков Е.В., Унтила Т.Н. Набережные челны: КамПИ, 2005, – 38с., 3ил.
Ил.: 3. Библ. 6 назв.
Рецензент: кандидат технических наук Сабиров И.С.
Печатается по решению научно–методического совета Камской государственной инженерно–экономической академии
© Камская государственная инженерно–экономическая академия, 2005.
Содержание
Лабораторная работа №1 ВЫЧИСЛЕНИЕ ЗНАЧЕНИЯ ФУНКЦИИ sin(x), РАЗЛОЖЕННОЙ В РЯД... 4
Теоретические основы... 4
Задание.. 5
Контрольные вопросы... 5
Лабораторная работа №2 НАХОЖДЕНИЕ МАКСИМУМА И МИНИМУМА В МАССИВЕ 5
Теоретические основы... 6
Задание.. 6
Контрольные вопросы... 6
Лабораторная работа №3 СОРТИРОВКА ЭЛЕМЕНТОВ МАССИВА... 7
Теоретические основы... 7
Задание.. 14
Контрольные вопросы... 14
Лабораторная работа №4 МЕТОДЫ ВЫЧИСЛЕНИЯ ЗНАЧЕНИЙ ПОЛИНОМА 14
Теоретические основы... 15
Задание.. 16
Контрольные вопросы... 16
Лабораторная работа №5 ВЫЧИСЛЕНИЕ ОПРЕДЕЛИТЕЛЯ МАТРИЦЫ ПРИВЕДЕНИЕМ К ТРЕУГОЛЬНОМУ ВИДУ... 16
Теоретические основы... 16
Задание.. 19
Контрольные вопросы... 19
Лабораторная работа №6 РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ МЕТОДОМ ГАУССА... 19
Теоретические основы... 20
Задание.. 21
Контрольные вопросы... 21
Лабораторная работа №7 ПРИБЛИЖЕННОЕ РЕШЕНИЕ УРАВНЕНИЯ ¦(x) = 0 21
Теоретические основы... 21
Задание.. 26
Контрольные вопросы... 26
Лабораторная работа №8 МИНИМИЗАЦИЯ ФУНКЦИИ... 26
Теоретические основы... 26
Задание.. 34
Контрольные вопросы... 34
Приложение 1 УСЛОВНЫЕ ОБОЗНАЧЕНИЯ ЭЛЕМЕНТОВ БЛОК–СХЕМ АЛГОРИТМОВ 35
Литература... 38
Лабораторная работа №1 ВЫЧИСЛЕНИЕ ЗНАЧЕНИЯ ФУНКЦИИ sin(x), РАЗЛОЖЕННОЙ В РЯД
Цель работы: Написать программу для вычисления значения функции sin(x) разложением в ряд. Получить навыки вычисление рекуррентных формул
Теоретические основы
Как правило, при решении задачи приходится вычислять значения элементарных функций (тригонометрических, показательных, логарифмических и др.). При ручном счете для этой цели могут быть использованы таблицы. Однако в вычислениях на ЭВМ ввод таблиц функций в машину потребовал бы больших затрат памяти. Кроме того, поиск нужного значения функции в памяти ЭВМ – не простое для машины занятие. Поэтому для вычисления значений функций на ЭВМ используются разложения этих функций в степенные ряды. Например, функция sin(x) вычисляется с помощью ряда:
При известном значении аргумента х значение функции может быть получено с точностью до погрешностей округления. Количество используемых членов ряда зависит от значения аргумента. Напомним, что в соответствии с правилами приближенных вычислений для предотвращения влияния погрешностей округления необходимо, выполнение неравенства 
.
С помощью степенных рядов вычисляются значения и других элементарных функций. В частности, для вычисления значений функции cos(x)можно использовать ряд sin(x) с учетом соотношения:
Для выполнения однотипных вычислений использующих в качестве исходных значений результаты, полученные в предыдущих вычислениях используют рекуррентные формулы. Так значения числителя и знаменателя элементов сумм ряда могут быть получены при домножении числителя на 
, а знаменателя на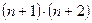 
, где n – текущий элемент факториала.
Например:
| 
|
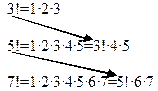
Выполнять цикл вычисления элементов ряда до тех пор пока их значение не станет меньше ε.
Задание
1. Написать программу для вычисления значений функций sin(x) или cos(x) разложенных в ряд, сравнить со значением, вычисленным с помощью стандартной тригонометрической функции;
2. Определить количество элементов ряда, при котором значения суммы ряда и функции будут совпадать с точностью до ε.
Контрольные вопросы
Лабораторная работа №2 НАХОЖДЕНИЕ МАКСИМУМА И МИНИМУМА В МАССИВЕ
Цель работы: Получить навыки работы с массивами данных. Написать программу для нахождения максимального и минимального элементов массива
Теоретические основы
Массив – это последовательность данных, записанная в определенной области памяти, обращение к которым осуществляется по их индексу. Данные, хранимые в массиве, могут быть различного типа как строковые (символьные), так и числовые (целые и вещественные).
Массив бывает одномерным (вектор) и n – мерным. Размерность определяется количеством индексов, с помощью которых происходит доступ.
В Visual Basic n – мерный массив определяется как
Dim Mas (a,…, n) As Type
где Mas – название переменной, по которой будет происходить обращение к массиву;
a,…,n – размерность массива;
Type – тип хранимых в массиве данных.
Нахождение минимального и максимального элементов массива происходит последовательным сравнением всех элементов массива с «эталоном». В качестве первого значения «эталона» обычно применяют первый элемент массива. В случае если «эталон» оказывается больше текущего элемента при нахождении минимума (меньше при нахождении максимума), то «эталону» присваивают значение текущего элемента и продолжают перебор значений до последнего элемента.
Задание
1. Написать программу для нахождения максимального и минимального элементов n –мерного массива, массив должен отображаться;
2. Преобразовать программу для нахождения 3–х наибольших элементов массива.
Контрольные вопросы
