Сортировка методом прямого включения, так же, как и сортировка методом простого выбора, обычно применяется для массивов, не содержащих повторяющихся элементов.
Сортировка этим методом производится последовательно шаг за шагом. На k –м шаге считается, что часть массива, содержащая первые k– 1 элемент, уже упорядочена, то есть 
.
Далее необходимо взять k –й элемент и подобрать для него место в отсортированной части массива такое, чтобы после его вставки упорядоченность не нарушилась, то есть надо найти такое 
что 
. Затем надо вставить элемент a(k) на найденное место.
С каждым шагом отсортированная часть массива увеличивается. Для выполнения полной сортировки потребуется выполнить n– 1 шаг.
Осталось ответить на вопрос, как осуществить поиск подходящего места для элемента х. Поступим следующим образом: будем просматривать элементы, расположенные левее х (то есть те, которые уже упорядочены), двигаясь к началу массива. Нужно просматривать элементы а(j), j изменяется от k– l до 1. Такой просмотр закончится при выполнении одного из следующих условий:
• найден элемент 
, что говорит о необходимости вставки х между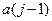 
и а(j).
• достигнут левый конец упорядоченной части массива, следовательно, нужно вставить х на первое место.
До тех пор, пока одно из этих условий не выполнится, будем смещать просматриваемые элементы на 1 позицию вправо, в результате чего в отсортированной части будет освобождено место под х.
Методику сортировки иллюстрирует таблица 2:
Таблица 2 – Пример сортировки с помощью прямого включения
Первоначально упорядоченная последовательность состоит из 1–го элемента 9. Элемент а( 2 ) =5 – первый из неупорядоченной последовательности и 5 < 9, поэтому ставится на его место, а 9 сдвигается вправо. Теперь упорядоченная последовательность состоит из двух элементов 5, 9. Элемент а( 3 ) =15 неупорядоченной последовательности больше всех элементов упорядоченной последовательности, поэтому остаётся на своём месте и на следующем шаге упорядоченная последовательность состоит из 5, 9, 15, а рассматриваемый элемент 6. Процесс происходит до тех пор, пока последовательность не станет упорядоченной.
Шейкерная сортировка
Метод пузырька допускает три простых усовершенствования. Во–первых, если на некотором шаге не было произведено ни одного обмена, то выполнение алгоритма можно прекращать. Во–вторых, можно запоминать наименьшее значение индекса массива, для которого на текущем шаге выполнялись перестановки. Очевидно, что верхняя часть массива до элемента с этим индексом уже отсортирована, и на следующем шаге можно прекращать сравнения значений соседних элементов при достижении такого значения индекса. В–третьих, метод пузырька работает неравноправно для "легких" и "тяжелых" значений. Легкое значение попадает на нужное место за один шаг, а тяжелое на каждом шаге опускается по направлению к нужному месту на одну позицию.
На этих наблюдениях основан метод шейкерной сортировки (ShakerSort). При его применении на каждом следующем шаге меняется направление последовательного просмотра. В результате на одном шаге "всплывает" очередной наиболее легкий элемент, а на другом "тонет" очередной самый тяжелый. Пример шейкерной сортировки приведен в таблице 3.
Таблица 3 – Пример шейкерной сортировки
Шейкерную сортировку рекомендуется использовать в тех случаях, когда известно, что массив "почти упорядочен".
Сортировка массива с помощью включений с уменьшающимися расстояниями (метод Шелла)
Д. Шеллом было предложено усовершенствование сортировки с помощью прямого включения.
Идея метода: все элементы массива разбиваются на группы таким образом, что в каждую группу входят элементы, отстоящие друг от друга на некоторое число позиций L. Элементы каждой группы сортируются. После этого все элементы вновь объединяются и сортируются в группах, при этом расстояние между элементами уменьшается. Процесс заканчивается после того, как будет проведено упорядочивание элементов с расстоянием между ними, равным 1.
Пример сортировки методом Шелла приведен в таблице 4.
Таблица 4 – Пример сортировки методом Шелла
Сначала рассмотрим вариант, когда первоначальное значение L равно половине числа элементов в массиве, а каждое последующее значение вдвое меньше предыдущего. Заметим, что обмениваются элементы, которые отстоят на величину шага. Если при сравнении 2–х элементов обмена не произошло, то места сравниваемых элементов сдвигаются вправо на одну позицию. Если обмен произошёл, то происходит сдвиг соответствующих сравниваемых элементов на L.
Сортировка разделением (быстрая сортировка)
Метод сортировки разделением был предложен Чарльзом Хоаром. Этот метод является развитием метода простого обмена и настолько эффективен, что его стали называть методом быстрой сортировки – «Quicksort».
Основная идея алгоритма состоит в том, что случайным образом выбирается некоторый элемент массива x, после чего массив просматривается слева, пока не встретится элемент a(i) такой, что a(i) > x, а затем массив просматривается справа, пока не встретится элемент a(i) такой, что a(i) < x. Эти два элемента меняются местами, и процесс просмотра, сравнения и обмена продолжается, пока мы не дойдем до элемента x. В результате массив окажется разбитым на две части – левую, в которой значения ключей будут меньше x, и правую со значениями ключей, большими x. Далее процесс рекурсивно продолжается для левой и правой частей массива до тех пор, пока каждая часть не будет содержать в точности один элемент. Рекурсию можно заменить итерациями, если запоминать соответствующие индексы массива.
Процесс сортировки массива быстрым методом представлен в таблице 5.
Таблица 5 – Пример быстрой сортировки
В большинстве утилит, выполняющих сортировку массивов, используется именно этот алгоритм.
Задание
1. Написать программы для сортировки массива всеми рассмотренными методами;
2. Сравнить эффективность методов сортировки.
Контрольные вопросы
