Бас инерция өстері мен бас инерция моменттері

x пен y координаттық өстерін u мен v орнына келтіріп бұрғанда, жазық қиманың инерция моменттері қалай өзгертінін қарастырайық. 10.4 суреттен келесіні анықтай аламыз

u = y∙ sin  + x ∙ cos ; v = y∙ cos   x∙ sin . (10.13) Осы өрнектерді

, , ескерілуімен түрлендіріп, келесіге келеміз

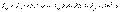, (10.14)

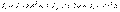, (10.15)

. (10.16)

Алдыңғы екі теңдеуді қосып, келесіні аламыз

(10.17) Сонымен, өзара перпендикуляр өстерге қатысты өстік инерция моменттерінің қосындысы өстер бұрылғанда тұрақты болып қалады және жазық фигураның полюстік инерция моментіне тең. (10.17) қолдануымен дөңгелек қиманың диаметріне қатысты өстік инерция моментін анықтауға болады. Симметрия себебінен , сонда (10.18)

 бұрышы өзгеруімен 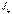және өзгереді, ал олардың қосындысы тұрақты болады, сондықтан олардың біреуін 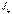немесе , өзінің максимал-ды мәніне, екіншісін минималды мәніне ие болдыратынбұрыштың =₀ мәнін табуға болады. ₀ табу үшін 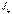немесе экстремумге зерттейміз. Сонда келесі табылады

. (10.19)

=₀ болғанда біржолы центрден тепкіш инерция моменті 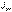нөлге тең болатынын көрсетуге болады. Егер өстерге қатысты центрден тепкіш инерция моменті нөлге тең, ал өстік инерция моменттері экстремалды мәндерін алатын болса, онда сол өстер бас инерция өстері деп аталады. Бас инерция өстеріне қатысты өстік инерция моменттері бас инерция моменттері деп аталады. Олар (10.14), (10.15) және (10.19) қолдануымен келесідей табылады

. (10.20)

Жазық фигураның кез келген l өсіне қатысты инерция радиусы деп келесі формуламен анықталатын шаманы атайды

. (10.21)

37. Таза иілу. Иілу кезіндегі ішкі күштер факторлары Иілу деп көлденең қималарында июші момент M пайда болатын сырықтың жүктелу түрін атайды. Егер сонда барлық ІКФ нөлге тең болса, онда таза иілу орын алады дейміз. Жиі M июші моментімен қатар Q көлденең күші болады, сонда көлденең иілу орын алады. Иілу есептерін шешуінде ішкі күштер факторларының эпюрлерін тұрғызуды білу керек. Ол үшін қималар әдісі қолданылады. Деформацияға дейін өсі горизонталь орналасқан сырықтың оған түсірілген актив күштер вертикаль (yz) жазықтығында жататын жағдайдағы иілуін қарастырайық. Арқалықтың кез келген қимасындағы көлденең күш қиманың бір жағындағы (арқалықтың қарастырылатын қимамен кесіліп алынған бір бөлігіне түсірілген) сыртқы күштердің вертикаль өсіне проекцияларының қосындысына тең болады

. (10.22)

Көлденең күш үшін таңбалар ережесі: егер қиманың сол жағындағы сыртқы күштердің тең әсерлі күші төменнен жоғары қарай бағытталса (10.5,а сурет), онда Q оң шама, керісінше жағдайда теріс шама болады. Оң жақтағы бөлік үшін ереже қарсы болады. Июші момент қиманың бір жағындағы (арқалықтың қарастырылатын қимамен кесіліп алынған бір бөлігіне түсірілген) сыртқы күштердің сол қиманың көлденең өсіне қатысты моменттерінің қосындысына тең болады

. (10.23). Июші момент үшін таңбалар ережесі: M эпюрін сығылған талшық үстінде тұрғызады, яғни M ординатасын сырықтың серпімді сызығының ойыс жағына қарай көрсетеді (10.5, б сурет). Егер сыртқы күш (немесе күштер жұбы) сырықты дөңес жағымен төмен қарай майыстыруға тырысса, онда оның моментін (10.23) формуласында оң таңбасымен алу керек, керісінше жағдайда – теріс таңбасымен.