Динамика заңдары тек қана инерциалдық СЖ-нде орындалады. Материялық нүктенің кейбір СЖ-не қатысты қозғалысын қарастырайық және осы СЖ инерциалдық СЖ-не қатысты еркінше қозғалатын болсын. P нүктесі {  } күштер әсерінен қозғалатын болсын. Инерциалдық СЖ-нде динамиканың негізгі (5.2) теңдеуі орындалады. Нүктенің абсолют үдеуі (5.17) формуласымен табылады
} күштер әсерінен қозғалатын болсын. Инерциалдық СЖ-нде динамиканың негізгі (5.2) теңдеуі орындалады. Нүктенің абсолют үдеуі (5.17) формуласымен табылады
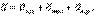 (5.5)
(5.5)
(5.5) теңдігін (5.4) теңдігіне қойып, түрлендіреміз
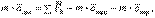 (5.6)
(5.6)
Келесі белгілерді қабылдаймыз
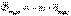 (5.7)
(5.7)
және  (5.8)
(5.8)
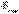 және
және  векторлары сәйкес тасымал және кориолис инерция күштері деп аталады.
векторлары сәйкес тасымал және кориолис инерция күштері деп аталады.
(5.6) теңдігін келесі түрде жазуға болады
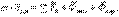 (5.9)
(5.9)
(5.9) теңдеуі МН-нің салыстырмалы қозғалысы динамикасының негізгі теңдеуі деп аталады. МН-нің салыстырмалы қозғалысының теңдеулері абсолют қозғалысының теңдеулері секілді, түсетін күштерге тасымал және кориолис инерция күштерін қосып, құрастырылады. Қозғалатын инерциалдық емес СЖ-нің бақылаушы тасымал және кориолис инерция күштерін шынайы әсер ететін күштер секілді қабылдайды. Бірақ ол дұрыс емес, өйткені инерциалдық емес СЖ үшін механиканың Ньютон заңдары орындалмайды, сондықтан құбылыстарды алдыңғы аксиомалар қолдануымен қарастыруға болмайды.
МН-нің салыстырмалы қозғалысы негізгі теңдеуінің дербес жағдайлары: а) ілгерілемелі тасымал қозғалыс кезінде  (5.10)
(5.10)
б) түзу сызықты бірқалыпты тасымал қозғалыс кезінде
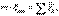 (5.11)
(5.11)
Мұнда (5.11) мен (5.2) бірдей болады, өйткені 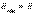 . Сондықтан, бұл санақ жүйесі инерциалдық болады. Механикалық тәжірибелер арқылы санақ жүйесі тыныштықта екенін немесе ілгерілемелі бірқалыпты және түзу сызықты қозғалыста екенін анықтау мүмкін емес (Галилейдің салыстырмалылық принципі);
. Сондықтан, бұл санақ жүйесі инерциалдық болады. Механикалық тәжірибелер арқылы санақ жүйесі тыныштықта екенін немесе ілгерілемелі бірқалыпты және түзу сызықты қозғалыста екенін анықтау мүмкін емес (Галилейдің салыстырмалылық принципі);
в) салыстырмалы тыныштық қалпында
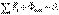 (5.12)
(5.12)
Бұл МН-нің салыстырмалы тепе-теңдігінің теңдеуі.
Нүктенің қозғалыс мөлшерінің өзгеруі туралы теорема. Динамиканың көптеген есептерін шешу кезінде ҚДТ-н интегралдаудың орнына динамиканың жалпы теоремаларын қолданған тиімділеу болады. Нүктенің қозғалыс мөлшерінің өзгеруі туралы теоремасын қарастырайық. МН-нің қозғалыс мөлшері деп нүктенің массасы мен оның жылдамдығының 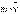 көбейтіндісіне тең шаманы айтады.
көбейтіндісіне тең шаманы айтады.  векторы нүктенің траекториясына жанама бағытталады.
векторы нүктенің траекториясына жанама бағытталады.
Күштің элементар импульсі деп күштің элементар уақыт аралығына көбейтіндісін атайды
 (5.13). Импульс күштің әсер ету сызығы бойымен бағытталады.
(5.13). Импульс күштің әсер ету сызығы бойымен бағытталады.  күшінің шекті t1 уақыт ішіндегі
күшінің шекті t1 уақыт ішіндегі 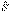 импульсі
импульсі  (5.14). Импульстің модулі мен бағытын оның проекциялары арқылы табуға болады
(5.14). Импульстің модулі мен бағытын оның проекциялары арқылы табуға болады
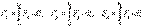 . (5.15)
. (5.15)
Динамиканың негізгі теңдеуін келесі түрде жазуға болады  (5.16)
(5.16)
Бұл дифференциалдық түрдегі нүктенің қозғалыс мөлшерінің өзгеруі туралы теоремасы: нүктенің қозғалыс мөлшерінің уақыт бойынша туындысы нүктеге түсетін күштердің векторлық қосындысына тең. Шекті түрдегі сол теорема: нүктенің қозғалыс мөлшерінің кейбір уақыт аралығында өзгеруі оған түсетін күштердің сол уақыт аралықтағы импульстерінің векторлық қосындысына тең
 . (5.17)
. (5.17)
Есептерді шешу кезінде әдетте теңдеулердің проекциялары қолданылады.
Нүктенің қозғалыс мөлшері моментінің өзгеруі туралы теорема. Нүктенің қозғалыс мөлшерінің кейбір О центріне қатысты моменті деп келесі теңдікпен анықталатын 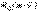 векторлық шамасын айтады
векторлық шамасын айтады
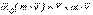 (5.18)
(5.18)
мұндағы 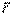 - қозғалыстағы нүктенің О центрінен жүргізілген радиус-векторы.
- қозғалыстағы нүктенің О центрінен жүргізілген радиус-векторы.
Сонда 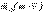 векторы
векторы 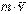 және О центрі арқылы өтетін жазықтыққа перпендикуляр бағытталады, aл модулі
және О центрі арқылы өтетін жазықтыққа перпендикуляр бағытталады, aл модулі  .
.
Нүктенің қозғалыс мөлшерінің О центрінен өтетін Оz өсіне қатысты моменті 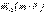 векторының сол өске проекциясына тең
векторының сол өске проекциясына тең
 (5.19)
(5.19)
мұндағы -  векторы мен Оz өсі арасындағы бұрыш.
векторы мен Оz өсі арасындағы бұрыш.
Теорема: нүктенің қозғалыс мөлшерінің кейбір қозғалмайтын центрге қатысты алынған моментінің уақыт бойынша туындысы әсер ететін күштің сол центрге қатысты моментіне тең
 (5.20)
(5.20)
Өске қатысты моменттер теоремасы
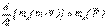 . (5.21)
. (5.21)
(5.20) теңдеуінен 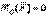 болса,
болса, 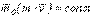 болатыны шығады.
болатыны шығады.
17. Күштің жұмысы мен қуаты. Нүктенің кинетикалық энергиясының өзгеруі туралы теорема. М нүктесіне түсетін  күшінің (5.1 сурет) элементар жұмысы деп, келесі скаляр шаманы айтады dW = F ∙ds (5.22)
күшінің (5.1 сурет) элементар жұмысы деп, келесі скаляр шаманы айтады dW = F ∙ds (5.22)
мұндағы F - 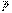 күшінің М нүктесінің траекториясына нүктенің орын ауыстыру бағытымен жүргізілген М жанамасына проекциясы; ds - М нүктенің элементар орын ауыстыруының модулі. ds=|d
күшінің М нүктесінің траекториясына нүктенің орын ауыстыру бағытымен жүргізілген М жанамасына проекциясы; ds - М нүктенің элементар орын ауыстыруының модулі. ds=|d  | болғандықтан (мұндағы d
| болғандықтан (мұндағы d  - нүктенің элементар орын ауыстыру
- нүктенің элементар орын ауыстыру  векторы), (5.22) теңдігін келесі түрде жазуға болады dW=
векторы), (5.22) теңдігін келесі түрде жазуға болады dW= 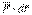 . (5.23) Сонымен, күштің элементар жұмысы күштің оның түсу нүктесінің орын ауыстыру векторына скаляр көбейтіндісіне тең. Күштің шекті M0M1 орын ауыстыруында (5.1 сурет) жұмысы төмендегідей анықталады
. (5.23) Сонымен, күштің элементар жұмысы күштің оның түсу нүктесінің орын ауыстыру векторына скаляр көбейтіндісіне тең. Күштің шекті M0M1 орын ауыстыруында (5.1 сурет) жұмысы төмендегідей анықталады
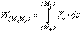 , (5.24)
, (5.24)
 (5.25)
(5.25)
Күштің қуаты деп күштің уақыт бірлігінде жасайтын жұмысына тең шаманы айтады. Егер жұмыс бірқалыпты жасалатын болса, онда қуат P = W/t1 (мұнда t1 – W жұмысы жасалатын уақыт аралығы). Жалпы жағдайда
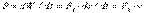 (5.26)
(5.26)
яғни қуат күштің жанама құраушысының жылдамдыққа көбейтіндісіне тең.
Нүктенің кинетикалық энергиясы (КЭ) деп  тең скаляр шаманы айтады. Теорема: нүктенің КЭ оның кейбір орын ауыстыру кезіндегі өзгерісі нүктеге түсетін барлық күштердің сол орын ауыстырудағы жұмыстарының алгебралық қосындысына тең
тең скаляр шаманы айтады. Теорема: нүктенің КЭ оның кейбір орын ауыстыру кезіндегі өзгерісі нүктеге түсетін барлық күштердің сол орын ауыстырудағы жұмыстарының алгебралық қосындысына тең
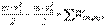 . (5.26)
. (5.26)






