Нүкте үшін Даламбер принципі

Массасы m материялық нүктеге тең әсерлі күші 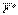деп белгіленген актив күштер және байланыстың 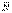реакциясы түсетін болсын. Осы күштер әсерінен нүкте инерциалдық СЖ-не қатысты кейбір 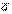үдеуімен қозғалады.

Келесі шаманы енгіземіз

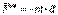(5.27)

ол күштің өлшем бірлігіне ие болады. Модулі нүкте массасы мен оның үдеуінің көбейтіндісіне тең және сол үдеуге қарама-қарсы бағытталатын векторлық шама нүктенің инерция күші деп аталады. Сонда, егер кез келген уақыт мезгілінде нүктеге түсетін актив және реакция күштеріне инерция күшін қосса, алынған күштер жүйесі теңгеріледі, яғни

. (5.28)

Бұл МН үшін Даламбер принципін өрнектейді.

 

Механикалық жүйе. Масса, массалар центрі және инерция моменттері

Механикалық жүйе (МЖ) деп өзара әрекеттесетін МН-лердің немесе денелердің жиынтығы аталады. Материалық дене оны құрайтын бөлшектердің МЖ-сі болып келеді. Нүктелерінің қозғалысы байланыстармен шектелмейтін МЖ еркін материялық нүктелердің жүйесі деп аталады. Жүйенің нүктелеріне қарастырылып отырған жүйеге кірмейтін денелерден түсетін 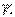, k= 1,2 …,n күштері сыртқы күштер деп аталады. Ішкі күштер деп жүйе нүктелері бір- біріне түсіретін 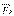, k= 1,2 …,m күштері аталады. Ішкі күштер жүйесінің бас векторы мен бас моменті нөлге тең болатынын көрсетуге болады. Бұдан ішкі күштер жалпы жағдайда теңгерілетіні шықпайды, өйткені олардың әсерінен жүйе нүктелерінің орын ауыстырулары болуы мүмкін (АҚД үшін теңгеріледі). Жүйе массасы деп жүйе нүктелері массаларының қосындысын атайды

M=Σm_k. (6.1). Жүйенің массалар центрінің орны (С нүктесі) келесі формулалармен анықталады

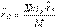, (6.2)

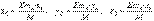(6.3)

Дене үшін келесі болады

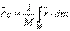, (6.4)

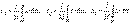. (6.5)

Ауырлық күштердің біртекті өрісінде массалар мен ауырлық центрлері түйіседі. МЖ-нің өске және нүктеге қатысты инерция моменттері деп келесі шамалар аталады

J_l=Σm_k∙h_k². (6.6)

J_O=Σm_k∙r_k² (6.7)

мұндағы h_k мен r_k – дененің массасы m_k нүктесінің l өсіне дейінгі және O нүктесіне дейінгі қашықтытары. Қатты дене үшін өске және нүктеге қатысты инерция моменттері

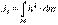, (6.8)

. (6.9)

Декарт өстеріне және координаттар басына қатысты инерция моменттері

J_x=Σm_k∙(y_k²+z_k²), J_y=Σm_k∙(x_k²+z_k²), J_z=Σm_k∙(x_k²+y_k²), (6.10)

J_O=Σm_k∙r_k²= Σm_k∙(x_k²+y_k²+z_k²). (6.11)

Координаттық жазықтықтарға қатысты инерция моменттері келесіге тең J_xy=Σm_k∙ z_k², J_yz=Σm_k∙x_k², J_xz=Σm_k∙y_k². (6.12)

Келесі тәуелдіктер орын алатынын дәлелдеуге болады 2J_O= J_x+ J_y+ J_z, (6.13)

J_O= J_xy+ J_yz+ J_xz. (6.14)

Дене үшін инерция моменттері массалар бойынша интегралдармен анықталады

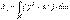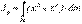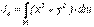, , . (6.15)

Гюйгенс-Штейнер теоремасы: жүйенің кейбір z өсіне қатысты J_z инерция моменті сол өске параллель, массалар центрінен өтетін z_C өсіне қатысты жүйенің J_zC инерция моментінің және жүйенің M массасының өстердің d арақашықтығына көбейтіндісінің қосындысына тең

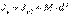. (6.16). Параллель өстер жиынтығы арасында массалар центрінен өтетін өске қатысты инерция моменті ең кіші болады.