Ішкі күштердің қимада таралуын сипаттау үшін кернеу ұғымы енгізіледі. S қимасының К нүктесіндегі толық кернеу векторы деп, келесі шама аталады
(7.1)
мұндағы 
- K нүктесі аймағындағы элементар аудан; 
- элементар ауданға түсетін ішкі күштердің тең әсерлі күші. Сонымен, кернеу ауданның бірлігіне түсетін ішкі күш болып табылады (паскальмен өлшенеді). р кернеуін 3 құраушыға жіктеуге болады: қиманың нормалі бойымен (тік кернеуі) және қима жазықтығындағы екі өс бойымен (жанама 
кернеулері). Егер К нүктесі арқылы басқа қию ауданды жүргізсе, жалпы жағдайда кернеудің шамасы басқа болады. Нүктеден жүргізілген барлық аудандардағы кернеулердің жиынтығы нүктенің кернеулі күйін құрайды (ол 6 шамамен толық анықталады). Сыртқы күштер әсерінен барлық денелер өздерінің өлшемдері мен формасын өзгертеді (деформацияланады). Осы өзгерістер әдетте аз болса да ішкі күштердің дене бойымен таралуына айтарлықтай әсерін тигізеді. Деформациялану кезінде дене нүктелері кеңістікте өзінің орнын ауыстырады. Деформацияланбаған дене нүктесінен басталып, деформацияланған дененің дәл сол нүктесіне жүргізілген вектор нүктенің сызықты орын ауыстыру векторы деп аталады. Бұрыштық орын ауыстыру ұғымы келесідей енгізіледі: деформацияға дейін екі жақын нүктелердің арасындағы түзу кесінді де-формация болғаннан кейін кеңістікте кейбір бұрышқа бұрылады, ол да вектормен сипатталады. Егер жүйеге, оның кеңістікте қатаң бүтін ретінде орын ауыстыруына ешқандай мүмкіншілік бермеуге жеткілікті байланыстар енгізілген болса, онда жүйе кинематикалық өзгермейтін жүйе деп аталады. МК-нде әдетте тек сондай жүйелер қарастырылады. Керісінше жағдайда орын ауыстырулардың тек қана деформациялар себебінен бола-тын бөлігі қарастырылады. Сонда көптеген жүйелер үшін кез келген нүктенің орын ауыстыруы дене өлшемдерімен салыстырғанда өте аз шама болады. Сондықтан, статика теңдеулерін құрған кезде бастапқы өлшемдер принципі бойынша өлшемдердің өзгеруі есепке алынбайды (бұдан өзгешеліктер бар). Дене өлшемдері мен формасының өзгеру қарқындылығын сипаттау үшін денені деформацияға дейін және деформация болғаннан кейін қарастырайық (7.4 сурет). Келесі шама
(7.2)
А нүктесінің АВ бағыты бойымен сызықтық деформациясы немесе деформациясы деп аталады (оның реті 10-3). Дәл сол нүктедегі басқа бағыты бойымен алынған деформация, жалпы айтқанда, басқа болады. х, у және z өстері бойымен 
деформацияларды х, у және z деп белгілейді.
Дене ішінде OD және ОС кесінділерімен жасалған тік бұрышты қарастырайық (7.4 сурет). Дене сыртқы күштермен жүктелген сон, бұл бұрыш өзгеріп, C'O'D' мәніне ие болады. Келесі шама
(7.3)
О нүктесіндегі COD жазықтығындағы бұрыштық деформация немесе ығысу бұрышы деп аталады. Координаттық жазықтықтарда ығысу бұрыштар уz, zx және ху арқылы белгіленеді.
26. Сырықтардың созылуы мен сығылуы. Бойлық күш және тік кернеулер. Созылу деп, сырықтың көлденең қималарында тек қана N бойлық күші орын алып, басқа ІКФ нөлге тең болатын сырықтың жүктелу түрін атайды. Созылу кезінде N күшінің бағыты қарастырылатын қиманың сыртқы нормалімен бірдей болады. Сығылу созылудан формалды түрде тек қана N күшінің бағытымен айырылғанмен, онда айтарлықтай айырмашылықтар бо-луы мүмкін (ұзын сырықтар сығылған кезде олар иілуі мүмкін, созылу және сығылу кезіндегі қирау міңезі әртүрлі болады). Әдетте созылу немесе сығылу сырық өсі бойымен бағытталған сыртқы күштер әсерінен пайда болады. N эпюрі қима әдісі қолдануымен тұрғызылады, сонда N күші қарастырылатын қиманың бір жағындағы сырық бөлігіне түсетін сыртқы күштердің бойлық өсіне проекцияларының қосындысына тең
N = ∑Fiz. (8.1)
Созатын N күші - оң, сығатын - теріс болып алынады. Сондықтан (8.1) формуласында сыртқы күш қимадан тыс бағытталса, оның проекциясы «+» таңбасымен, қимаға қарай бағытталса – «-» таңбасымен алынады. 8.1 сурет-те N эпюрінің тұрғызу мысалы көрсетілген. N күші көлденең қимадағы ішкі тік күштердің тең әсерлісі болып келеді, ол қимадағы тік кернеулерімен келесі тәуелдікпен байланысады 
(8.2), мұндағы σ – қиманың кез келген нүктесінің dA элементар ауданындағы тік кернеуі; A – көлденең қиманың ауданы.
Қиманың әр нүктесіндегі σ кернеуін табу үшін оның қима бойымен таралу заңын білу керек. 
Көлденең қимасы тұрақты, біртекті материалдан жасалған және шеттерінде түсірілген созу F күштерімен жүктелген сырықты қарастырайық (8.2 сурет). Жүктелу алдында оның бетінде өске перпен-дикуляр түзу сызықтарды жүргізейік. Тәжірибе көрсеткендей, жүктелу кезінде сол сызықтар түзу және өске перпендикуляр болып қала береді. Бұдан сырықтың жүктелу алдындағы жазық көлденең қималары жүктелу кезінде жазық болып қала береді деп есептеуге болады (жазық қималар гипотезасы). Бірдей ұзаруларға сәйкес бірдей кернеулер болғандықтан, көлденең қимасының барлық нүктелерінде кернеулер бірдей болады, сонда
бұдан 
(8.3)
Тік кернеу созылу кезінде оң, ал сығылу кезінде теріс болып есептеледі. Қарастырылатын мысалда біртекті кернеулі күй орын алады, яғни сырықтың барлық нүктелеріндегі кернеулі күй бірдей. Егер сырықтың қимасы айнымалы болса (8.3 сурет), онда ол дәл солай жүктелген кезде нүктелердегі кернеулі күйлер әр түрлі болады.
27. Созылу ж/е сығылу кезінде сырықтың ұзаруы және Гук заңы. Юнг модулі. Созылған сырықтың өлшемдері түсірілген күштерге тәуелді өзгереді. Мысалы, 8.2 суретте көрсетілген сырық сырықтың абсолют (толық) ұзаруы деп ата-латын ∆l шамасына ұзарады. Мұнда біртекті кернеулі күй болғандықтан, сызықты деформация (яғни салыстырмалы ұзаруы) барлық нүктелерде бірдей және келесіге тең
. (8.4)
Біртекті емес кернеулі күй жағдайында (8.3 сурет)
(8.5)
Аз ε шектерінде көптеген материалдар үшін Гук заңы орындалады (σ мен ε арасындағы сызықты тәуелдік) σ=Е∙ε (8.6), мұндағы E –Юнг модулі (I ретті серпімділік модулі). Юнг модулі тәжірибе арқылы анықталады. (8.5) формуласын (8.3) және (8.4) ескеруімен интегралдаудан кейін келесіге келемі
.(8.7) Көлденең қимасы тұрақты және шеттерінде F күштерімен жүктелген сырық үшін N=F=const боладыжәне абсолют ұзаруы келесіге 
тең 
.(8.8) Мұнда E∙А – сырықтың созылу-сығылу кезіндегі қатаңдығы. Егер серпімді деформациялармен қатар температуралық деформация-ларды есепке алу керек болса, онда қосынды деформация осылай анықталады
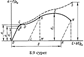
(8.9), мұндағы α – материалдың температуралық ұлғаю коэффициенті; ∆ t – температураның өсімі.
Сырықтың жәй (статикалық) жүктелу кезінде сыртқы күштердің жұмысы толығымен деформацияның U потенциялық энергиясына айналады, ол Гук заңы орындалғанда келесі түрде жазылады
. (8.10)
Көлденең қимасы тұрақты, біртекті материалдан жасалған және шеттерінде күштермен жүктелген сырық жағдайында келесі орын алады
. (8.11)
28. Созылу кезіндегі кернеулі және деформациялық күйлер. Сырықтың көлденең қимасымен α бұрышын жасайтын көлбеу қимала-рындағы кернеулерді қарастырайық (8.6, а сурет). Егер көлденең қимасының ауданы A болса, онда көлбеу қимасының ауданы A/cosα болады. 8.6, б суреттен p∙Aα = F және F=σ∙A болатыны көрінеді, сондықтан р = F/ Aα = σ∙cosα. (8.15) р кернеуін σ α және τ α құраушыларына жіктеп (8.5, в сурет), келесіні аламыз σα= р∙cosα = σ∙cos2α, (8.16)
τ α = р∙sinα = 
σ∙sin2α. (8.17)
Осыдан келесі орын алады:
а) α=0 болғанда (көлденең қималарында)σ α = σ , τ α =0; б) α=90 ْ(бойлық қималарында) σ α = 0 , τ α =0, яғни бойлық қабаттар өзара әрекеттеспейді;
в) α=45 ْболғанда τ кернеуі ең жоғары мәніне ие болады τ max = σ / 2; г) α және (α+90 ْ) бұрыштарымен орналасқан қималарда τ шамасының абсолют мәні бірдей; бұл жанама кернеулердің жұптылық заңы, ол әрқашанда орындалады. Созылу кезіндегі деформацияларды қарас-тырайық. Тәжірибе көрсеткендей, кейбір шек-терде сырықтың бойлық ұзаруымен қатар бір-жолы оған пропорционал көлденең жіңішкеру болады (8.7 сурет). Көлденең деформациясы ε´=∆а/а және
ε´=-µ∙ε (8.18). мұндағы µ - көлденең деформациясының коэффициенті (Пуассон коэф-фициенті); оның мәні металлдар үшін 0,25… 0,35 шектерінде жатады. Сырықта осымен қатар γα бұрыштық деформациялар орын алады (8.8 сурет). Сондаγα ығысу бұрышы сәйкес аудандағы τ α жанама кернеуіне пропор-ционал болатынын дәлелдеуге болады. Бұл – ығысу кезіндегі Гук заңы
τ=G∙γ (8.19)
мұнда G – ығысу модулі немесе II ретті серпімділік модулі.
Материал серпімділігінің Е, G және µ параметрлері арасында келесі өзара тәуелдігі орын алады
. (8.29)
29. Пластикалық материалд-ң созылу ж/е сығылу диаграммалары. Материалдар қасиеттерін зерттеу үшін және шекті кернеулердің мәндерін анықтау үшін материал үлгілерінің сынауларын оларды сындыруға дейін жүргізеді. Сынаулар статикалық, соққы және циклдік жүктемелер әсерінен созылуға, сығылуға, бұралуға және иіюлуге жүргізіледі (кейбірде күрделі қарсыласуға). Сынаудың нәтижелері үлгінің формасына, деформациялану 
жылдамдығына, сынау кезіндегі температураға және т.б. тәуелді болғандықтан, оларды арнаулы машиналарда стандартталған шарттар сақтауымен жүргізеді. Ең кеңінен таралған сынаулар – статикалық жүктеме әсерінен созылуға сынаулар, өйткені олар ең қарапайым болып келеді және материал деформацияның басқа түрлерін қалай қабылдайтыны туралы айтуға мүмкіншілік береді.
Сынаулар үшін цилиндрлік және жазық үлгілер қолданылады (8.8 сурет). Әдетте цилиндрлік үлгілердің өлшемдері d0=20 мм және l0=10d0 немесе l0=5d0 болып алынады. Сынау кезінде созатын F күші мен үлгінің Δ l ұзаруы арасындағы тәуелдіктің диаграм-масы жазылып отырады. Әртүрлі өлшемдерімен алынған үлгілер бойынша сынау нәтижелерін салыстыруға мүмкіншілік болу үшін F- Δ l диаграммасының σ-ε диаграммасы ретінде қарасты-рады. Бұл нақты емес, өйткені σ=F/A0 және ε=∆l/l0 алынады (A0, l0 – үлгінің көлденең қимасының бастапқы ауданы мен оның бастапқы ұзындығы). Нақты σ мен ε A және l шамаларының ағымды мәндері арқылы анықталу керек болғандықтан, бұл σ-ε диаграммасын шартты созылу диаграммасы деп атайды. 8.9 суретте үздіксіз сызықпен аз көміртекті болаттың шартты созылу диаграммасы көрсетілген. ОА аралығында кейбір пропорционалдық шегі деп аталатын σпц шамасына дейін ε деформациясы σ кернеуіне пропорционал өседі, яғни Гук заңы орындалады (Ст3 болат үшін σпц ≈ 200 МПа). Содан кейін диаграмма қисық сызықтыға айналады, сонда серпімділік шегі деп аталатын, σсер шамасына дейін материал өзінің серпімділік қасиетін сақтайды. σпц және σсер арасындағы айырмашылығы аз болғандықтан (Ст3 үшін σсер ≈ 210 МПа), оларды қолдану кезінде айырмайды. Жүктемені әрі қарай өсіріп тұрғанда, бір мезгілде (С нүктесі) деформациялар, жүктеме өспесе де өсе береді. Горизонталь СD аралығы аққыштық ауданы деп, ал сәйкес кернеу – σақ аққыштық (немесе 
жұмсару) шегі деп аталады (Ст3 үшін 240…400 МПа).
Содан кейін диаграмма жоғары кетеді, материал созуға қарсыласу қабілетіне қайта ие болады. Е нүктесінде ең жоғары шартты кернеуге жетеміз, ол σб беріктік шегі деп немесе уақытша қарсыласуы деп аталады(Ст3 үшін σб = 400…500 МПа). Сонда үлгіде мойнақ деп аталатын жергілікті жіңішкеру орын алады (8.3, б сурет). Үлгі мойнағындағы қимасының ауданы тез азаяды, соның себебінен күш пен σ шамалары төмен түседі. Үлгінің үзілуі ең кіші қимасы бойымен болады. Беріктік шегі үлгі үзілетін кездегі кернеуге тең емес. Егер созатын күштің A0 ауданына емес, мойынның ауданына қатынасын тапсақ, онда үзілу алдын-дағы (S нүктесінде) мойындағы σшын кернеуі σб кернеуінен айтарлықтай жоғары болады.
Материал беріктігінің қарастырылған сипаттамаларымен қатар сынау арқылы үлгі үзілгендегі δ салыстырмалы қалдық ұзаруын анықтайды, ол материалдың пластикалық қасиетінің сипаттамасы болып келеді
(8.21), мұндағы l 0 – үлгінің бастапқы есептеу ұзындығы; l 1– үлгі үзілгеннен кейін, оның есептеу ұзындығы. Ст3 үшін δ ≥24%, жоғары берікті болаттар үшін δ =(7…10)%. Бұл ұзаруы орташа алынады, шынайы ұзаруы үзілген жерде орын алады. Айтарлықтай үлкен пластикалық деформацияларды зерттеу үшін шынайы созу диаграммасын білу қажет (8.9 суреттегі OCS қисығы). Қарастырылған созылу диаграммасы пластикалық материалдарды, яғни қирамай тұрғанда айтарлықтай қалдық деформацияларға ие бола алатын мате-риалдарды сипаттайды. Пластикалық қасиеті жоғары материалдарға мыс, алюминий, латунь, аз көміртекті болат және т.б. жатады, пластикалық қасиеті аз материалдарға – легирленген болаттардың көпшілігі. Кейбір 
пластикалық материалдардың созылу диаграммаларында аққыштық ауданы болмайды; олар үшін шартты аққыштық шегі қолданылады - ол қалдық деформация-сының кейбір шамасына сәйкес келетін кернеу. σ0,2 шартты аққыштық шегі 0,2% тең қалдық деформациясына сәйкес болады. 8.12 суретте пластикалық материалдың типтік сығылу диаграммасы көрсетілген. Басында ол созу диаграммасымен бірдей болады, кейін тікшіл көтеріледі, үлгі жалпаяды және қирамайды. Пластикалық материалдар үшін соылзу және сығылу кезіндегі аққыштық шектері бірдей болады
Пластикалық қасиетіне керісінше морт қасиеті бар. Морт материалдар үшін δ шамасы 2-5%-дан аспайды. Морт материалдарға шойын, инструменттік болат, тас, бетон, шыны және т.б. жатады. Пластикалық және морт мате-риалдарға бөлу шартты екенін айта кету керек, өйткені сынау шарттарына (жүктелу жылдамдығына, темпе-ратураға) және кернеулі күйіне тәуелді морт материал-дардың биімділігі пластикалық материалдар секілді, ал пластикалық материалдардың биімділігі морт материалдар секілді болуы мүмкін. Мысалы, шойыннан жасалған үлгі жан-жақты сығу кезінде пластикалық қасиетіне ие болады. Ал болаттан жасалған қырнауы бар үлгі, оның δ қалдық деформациясы салыстырмалы кішкене болғанда сынады.
30. Морт материалдардың созылу ж/е сығылу диаграммалары. Мұнда үлгілер текше немесе биік емес цилиндрлер (h≤ 3d) түрінде алынады, керісінше иілу пайда болуы мүмкін. Өте қысқа үлгілерді де пайдалануға болмайды, өйткені шеткі беттеріндегі үйкеліс күштері бірталай әсерін тигізеді. Морт материалдар үшін сығылу диаграммасының түрі созу диаграммасымен бірдей болады. Диаграмма бойынша σб мен δ анықталады, сонда сығу кезіндегі беріктік шегі созылу кезіндегі беріктік шегінен әдетте артық болады.
31 Созылу-сығылу кезіндегі беріктік шарты. Есептердің үш түрі Созылуға және сығылуғасынаулары нәтижесінде алынған мате-риалдардың механикалық қасиеттерін конструкция элементтерін есептеу кезінде қалай қолдануға болатынын қарастырайық.
Ең кең таралған әдіс – кернеулер бойынша беріктікке есептеу әдісі. Осы әдісте есептеу конструкцияда орын алатын кернеулердің ең үлкен кернеуі бойынша жүргізіледі, максималды кернеу материал үшін шекті шамасынан аспау керек σmax<σшек, сонда беріктіктің кейбір кепілдігі ескерілу керек, сондықтан беріктік шарты келесі түрде орындалу керек
σmax≤[σ]. (8.22), мұнда [σ] – қауіпсіз кернеу, ол шекті кернеудің кейбір бөлігі ретінде анықталады
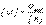(8.23), мұндағы [n] – беріктік кепілдігінің нормативтік мәні, ол конструкция жауапкершілігінің дәрежесіне, есептеу сұлбасының нақтылығына, жобалау тәжірибесіне, конструкция жұмысының шарттарына тәуелді беріледі. Сонда әрқашан [n] >1,0, оның мәндері конструкцияның әртүрлі элементтері үшін нормативтік құжаттарда беріледі. Конструкцияда білінетін қалдық деформациялар болмауы үшін пластикалық материалдардан жасалған конструкция элементтеріне σшек мәні созылған жағдайда 
, сығылған жағдайда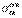 
тең деп алынады. Морт материалдарға және кейбір жағдайдабірыңғай пластикалық материалдарға σшек ретінде созылу немесе сығылу кезіндегі сәйкес 
немесе 
беріктік шегі алынады. Осы әдіс бойынша беріктік шартының басқа түрі
n≥[n] (8.24), мұндағы n – шынайы (есептеу) беріктік кепілдігі, ол n=σшек/σmax формуласымен анықталады. Сонымен, созылу-сығылу кезіндегі (8.22) беріктік шарты келесі түрге келтіріледі
.(8.25)
Беріктік шартын қолданып, келесі есептерді шешуге болады:
а) тексеру есептері. Мұнда берілген жүктеме мен сырықтың көлденең қимасының өлшемдері бойынша шынайы кернеулерді анықтап, оларды қауіпсіз кернеулермен салыстырады, сонда тікелей (8.4) шартының орындалуы тексеріледі. Кернеулер асып кетсе, беріктік қамсыздандырыл-майды, сондықтан мұндай жағдайға тыйым салынады, ал кернеулер аз болуы материалдың артық шығынына алып келеді; б) жобалау есептері. Берілген жүктеме мен қаупсіз кернеу бойынша беріктік шартын қанағаттандыратын сырықтардың көлденең қималарының өлшемдерін анықтайды
;(8.26), в) жүк көтеру шегін (жүк көтеру қабілетін) анықтау есептері. Мұнда сырық көлденең қимасының берілген өлшемдері мен берілген қауіпсіз кернеу бойынша қауіпсіз бойлық күшті анықтайды
, (8.27), содан кейін бойлық күш пен жүктеме арасындағы байланысты анықтап (статиканың тепе-теңдік теңдеулерінің қолдануымен), қауіпсіз жүктемені табуға болады.
Сығылған сырықтар беріктікке есептелуімен қатар орнықтылыққа да есептелу керек екенін айтқан жөн, өйткені сығушы күштің кейбір мәнінде сырық иіліп кетуі мүмкін (орнықтылықтан айырылу). Қауіпсіз кернеу әдісіндегі қабылданған критерий (нүктедегі кернеу) конструкция қирауының шарттарын кейбір жағдайларда сипаттамайтынын айтып кету керек. Сол жағдайларда критерий ретінде жүйе қирамай және формасын айтарлықтай өзгертпей, көтере алатын шекті жүктемені алған дұрыс.
32. Таза ығысу. Таза ығысу кезіндегі кернеулер мен деформациялар. 
Таза ығысу – денеден бөліп алынған элементтің беттерінде тек қана жанама кернеулері болатын кернеулі күй (9.1, а сурет). Біртекті таза ығысу жұқа қабырғалы цилиндрдің бұралу кезінде орын алады (9.2 сурет).
Егер таза ығысудағы эле-менттен оның бет-терімен 45º жасайтын беттері бар элементті қиып алсақ, оның беттерінде жанама кернеулер жоқ болып, тек қана тік кернеулер орын алатынын дәлелдеуге болады (9.1, б сурет). Сонда қарама-қарсы беттерінің бір жұбында кернеулер созушы (σ’=), екінші жұбында сығушы (σ”=-) болады. Алдында айтылғандай, жанама кернеуі мен γ бұрыштық деформациясы Гук заңы бойынша байланысады
=G∙γ. (9.1). Таза ығысу кезінде элементтердің қабырғаларының ұзындықтары өзгермейтінін және элемент қөлемінің өзгерісі де нөлге тең екенін дәлелдеуге болады. Материалдарды созылу мен сығылуға сынаулары секілді таза ығысуға да сынау жүргізіледі. Ол үшін моменттермен бұралатын жұқа қабырғалы құбыр тәрізді үлгілер қолданылады. Нәтижесінде мен γ координаттарындағы шартты ығысу диаграммасын алады, ол созу диаграммасына ұқсас болып келеді, сонда пластикалық металдар үшін аққыштық шегі ақ=(0,5…0,55)σақ. Таза ығысуға жақын кернеулі күй шегендерде, саңылаусыз қойылатын болттарда, шпонкаларда, шлицаларда, пісірілмелі біріктірмелерде орын алады.
33. Көлденең қимасы дөңгелек көлденең қималы сырықтың бұралуы. Бұралу - сырықтың көлденең қималарында тек қана Мбұр бұраушы моменты орын алып, басқа ІКФ нөлге тең болатын сырықтың жүктелу түрі. Бұралу әдетте сырық, әсер ету жазықтықтары сырықтың өсіне перпендикуляр күштер жұптарымен (бұрайтын моменттермен) жүктелген кезде орын алады. Бұраушы моменттердің эпюрін қималар әдісі қолдануымен тұрғызады, сонда Мбұр қарастырлатын қиманың бір жағындағы бөлікке түсірілген күштер жұптарының сырықтың бойлық өсіне қатысты моменттерінің қосындысына тең болады Мбұр = 
∑Mi. (9.2)
Таңбалар ережесі: егер қиманың сырт-қы нормалі жағынан қарағанда Мбұр сағат тілінің қозғалысына қарсы бағытталса, ол оң, керісінше жағдайда теріс болып есептеледі. Сонда (9.2) формуласының оң жағындағы сыртқы моменттер қарсы ережемен алыну керек. 9.3 суретте Мбұр эпюрін тұрғызу мысалы көрсетілген.
|
Сырықты (білікті) есептеуінде әдетте сыртқы моменттердің шамаларына тәуелді кернеулер мен бұ-рыштық орын ауыс-тыруларды анықтау керек. МК-нің әдісте-рімен тек қана көл-денең қималарының пішіні дөңгелек немесе сақина тәрізді сырық үшін (біз тек осы жағдайды қарастырамыз) және жұқа қабырғалы сырықтар үшін шешім табылады. Көлденең қимасы дөңгелек болып табылатын сырық жағдайында оның әр көлденең қимасы өзі-нің жазықтығында қатты диск секілді кейбір бұрышқа бұрылады деп есептейміз (жазық қималар гипотезасы). Шеттеріне M моменттері түсірілген, көлденең қимасының пішіні дөңгелек сырықты қарастырайық (9.4, а сурет). Оның көлденең қималарында тұрақты Мбұр=M бұраушы момент орын алады. Екі көлденең қима арқылы сырықтан ұзындығы dz элементті қиып аламыз, ал одан және ( + d) радиустерімен екі цилиндрлік беттер арқылы, элементар сақинаны қиып аламыз (9.4, в сурет). Бұралу нәтижесінде сақинаның оң жақ қимасы dφ бұрышына бұрылады. Сонда цилиндрдің АВ жасаушысы бұрышына бұрылып, АВ орнын алады. BВ доғасы бірінші жақтан ∙d тең, екінші жақтан ∙ dz тең. Сондықтан,
. (9.3). бұрышы жанама кернеулері әсерінен цилиндрлік беттің ығысу бұры-шы болып келеді. Келесі шама
(9.4) салыстырмалы бұралу бұрышы деп аталады. Бұл екі қиманың өзара бұрылу бұрышының олардың арақашықтығына қатынасы. (9.3) және (9.4) формулаларынан келесі 
алынады
= ∙θ. (9.5)
Ығысу кезіндегі Гук заңы бойынша
τ=G ∙∙θ (9.6)
мұндағы сырықтың көлденең қимасындағы жанама кернеулер. Олар-ға жұпталатын кернеулер бойлық жазықтарда орын алады (9.4, г сурет). 
Келесі тәуелдік болатыны анық (9.5 сурет) 
. (9.6) 
ескерумен аламыз. Мұндағы интеграл қиманың тек геометриялық сипаттамасы болып келеді, ол қиманың полюстік инерция моменті деп аталады
. (9.7) Сонымен, 
немесе
. (9.8)
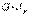шамасы сырықтың бұралу кезіндегі қатаңдығы деп аталады. (9.8) формуласынан (9.4) ескеруімен мынаны аламыз
. (9.9)
Егер Мбұр мен 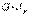сырық бойымен тұрақты болса, онда (9.9) формуласынан келесіге келеміз
. (9.10)
(9.8) формуласын (9.6)-ға қойып, кернеулердің өрнегін аламыз
(9.11)
Сонымен, жанама кернеулер радиус бойымен сызықты заңмен таралады, олардың максималды мәндері центрден ең алыста жатқан нүктелерінде болады. Сонда
немесе 
. (9.12)
Келесі шама 
(9.13)
сырықтың көлденең қимасының полюстік қарсыласу моменті деп аталады. (9.10), (9.12) формулалары дөңгелек және сақина тәрізді қималар үшін орын алады. Дөңгелек қиманың полюстік инерция моментін (9.7) қолдануымен, элементар ауданы dA=2π∙ρ∙dρ тең деп алып, таба аламыз (9.4 сурет). Сонда
немесе 
. (9.14)
Дөңгелек қиманың полюстік қарсыласу моментін табамыз
. (9.15)
Сақина тәрізді қима үшін (сыртқы диаметрі D және ішкі диаметрі d болса) келесіні аламыз
. (9.16)
(9.17)
34.Бұралу кезіндегі беріктік және қатаңдық шарттары келесі түрде жазылады
, (9.18)
немесе 
(9.19)
мұндағы [τ], [φ], [θ] – сәйкес қауіпсіз жанама кернеу, қауіпсіз толық және қауіпсіз салыстырмалы бұралу бұрыштары.
35. көлденең қимал-ң геометриялық сипаттамалары. Жазық фигуралардың статикалық моменттері мен оның ауырлық центрі. Кейбір жазық фигураны x, y координат жүйесінде қарастырайық 
(10.1 сурет). Келесі интегралдар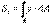 
, 
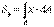(10.1), фигураның сәйкес x және y өстеріне қатысты ста-тикалық моменттері деп аталады.Координаттық өстерді параллель орын ауыс-тырса, қиманың статикалық моменттері қалай өзге-ретінін анықтайық (10.2 сурет ). x2 = x1 - a; y2 = y1 – b болатыны анық. Сонда
,
.
а мен b шамаларын, 
мен 
статикалық моменттері нөлге тең болатындай, таңдап алуға болады (тек бір ғана ретімен). Центрлік өс деп оған қатысты статикалық момент нөлге тең болатын өсті атайды. Центрлік өстерінің қиылысу нүктесі қиманың ауырлық центрі деп аталады. (x1, y1) координат жүйесінде ауырлық центрінің координаттары осыған тең
, 
(10.2)
Құрама қиманың статикалық моменті оны құраушы аймақтарының статикалық моменттерінің қосындысына тең екенін айтып өтейік.
