Базовый уровень
1. 1 Задание {{1}} ТЗ № 1
Порядок дифференциального ур-я определяется..
R порядком старшей производной
2. Задание {{1}} ТЗ № 1
Определить порядок дифференциального ур-я x 
R 2
3. Задание {{1}} ТЗ № 1
Определить порядок дифференциального ур-я 
R 1
4. Задание {{1}} ТЗ № 1
График решения дифференциального ур-я называется…
R Итегральной кривой
5. Задание {{1}} ТЗ № 1
Для дифференциального ур-я n-го порядка семейство функций γ(x,c 
,c 
,…c 
, любое решение ур-я можно получить выбирая значения
произвольных постоянных называется
R общим решением диф. ур-я
6. Задание {{1}} ТЗ № 1
Решением дифференциального ур-я 
является функцией
R 
R y=cosx
7. Задание {{1}} ТЗ № 1
Задача, состоящая в нахождении частного решения диф. ур-я по заданным начальным условиям называется…
R задачей Коши
8. Задание {{1}} ТЗ № 1
Из общего решения диф. ур-я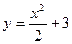 
найти частное решение, удовлетворяющее условию y(0)=3
R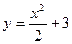 
9. Задание {{1}} ТЗ № 1
Укажите общее решение линейного однородного дифференциального уравнения 
:
R 
Средний уровень
10. Задание {{1}} ТЗ № 1
Укажите характеристическое уравнение для дифференциального уравнения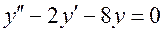 
:
R 
11. Задание {{1}} ТЗ № 1
Укажите общее решение линейного однородного дифференциального уравнения :
R
12. Задание {{1}} ТЗ № 1
Укажите характеристическое уравнение для дифференциального уравнения :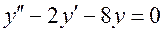
R
J 
13. Задание {{1}} ТЗ № 1
Дифференциальное уравнение первого порядка называется линейным, если его можно записать в виде
R 
14. Задание {{1 }} ТЗ № 1
Укажите общее решение линейного однородного дифференциального уравнения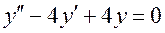 
:
R 
15. Задание {{ 1}} ТЗ № 1
Укажите характеристическое уравнение для дифференциального уравнения 
:
R 
16. Задание {{ 1}} ТЗ № 1
Укажите общее решение линейного однородного дифференциального уравнения 
:
R 
17. Задание {{ 1 }} ТЗ № 1
Общее решение линейного однородного дифференциального уравнения y ¢¢ – 4y ¢ + 3y = 0 имеет вид
R y(x) = C1ex + C2e3x
18. Задание {{ 1 }} ТЗ № 1
Общее решение линейного однородного дифференциального уравнения y ¢¢ + 4y ¢ + 4y = 0 имеет вид
R y(x) = e-2x (C1 + C2x)
19. Задание {{ 1 }} ТЗ № 1
Их данных диф. ур-й линейными неоднородными уравнениями 1го порядка являются…
R 
R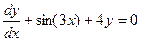 
20. Задание {{ 1 }} ТЗ № 1
Общий интеграл дифференциального уравнения 
имеет вид
R tgy=-e 
+c
21. Задание {{ 1 }} ТЗ № 1
Их данных диф. ур-й линейными неоднородными уравнениями 1го порядка являются…
R 
R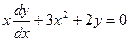 
22. Задание {{ 1 }} ТЗ № 1
Общий интеграл дифференциального уравнения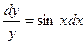 
имеет вид…
R ln|y|=- cosx+c
23. Задание {{ 1 }} ТЗ № 1
Общий интеграл дифференциального уравнения 
R arcsin y= 
24. Задание {{ 1 }} ТЗ № 1
Из данных диф. ур-й разделяющимися переменными являются…
R 
R 
Высокий уровень
25. Задание {{ 1 }} ТЗ № 1
Общее решение линейного однородного дифференциального уравнения y ¢¢ + y = 0 имеет вид
R y(x) = C1cosx + C2sinx
26. Задание {{ 1 }} ТЗ № 1
Общее решение линейного однородного дифференциального уравнения y ¢¢ –4y ¢ +5y=0 имеет вид
R y(x) = e2x (C1cosx + C2sinx)
27. Задание {{ 1 }} ТЗ № 1
Решение ур-я 
является функцией…
R y= 
28. Задание {{ 1 }} ТЗ № 1
Решение уравнения 
является функция
R y= 
29. Задание {{ 1 }} ТЗ № 1
Решением уравнения 
=1 является функция…
R y= 
30. Задание {{ 1 }} ТЗ № 1
Установить соответствие между видом правой части f(x) и видом частного решения 
дифференциального ур-я 
F(x)=x 
F(x)=x 
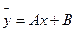
F(x)=e 
F(x)=2 
Ряды
Базовый уровень
1. Задание {{ 720 }} Укажите ряд Тейлора функции 
в окрестности точки а:
R 
2. Задание {{ 720 }} ТЗ № 20
Укажите ряд для функции 
:
R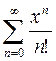 
3. Задание {{ 720 }} ТЗ № 20
Ряд 
расходится, если
R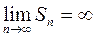 
4. Задание {{ 720 }} ТЗ № 20
Укажите общий вид степенного ряда:
R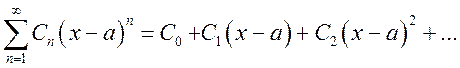 
5. Задание {{ 1 }} ТЗ № 1
Укажите ряд Маклорена:
J 
;
R 
;
6. Задание {{ 1 }} ТЗ № 1
Ряд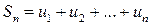 
сходится, если
J 
;
R2) 
;
R3) 
;
R4)* 
.
7. Задание {{ 1 }} ТЗ № 1
«если для знакоположительного ряда 
найти предел 
,
то при L>1 ряд сходится»- это утверждение называется…
R признаком Даламбера
8. Задание {{ 1 }} ТЗ № 1
«Если знакоположительного ряда существует предел 
, то при е<1 ряд сходиться, при е>1- расходится»- это утверждение называется
R признаком Коши
Средний уровень
9. Задание {{ 1 }} ТЗ № 1
Установите соответствие м\у знакопеременными рядами видами сходимости
Абсолютно сходится 
Условно сходится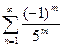 
Расходятся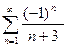 
10. Задание {{ 1 }} ТЗ № 1
Установите соответствие м\у знакопеременными рядами видами сходимости
Абсолютно сходится 
Условно сходится
Расходятся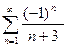
11. Задание {{ 1 }} ТЗ № 1
Установите соответствие м\у знакопеременными рядами видами сходимости
Абсолютно сходится 
Условно сходится 
Расходятся 
12. Задание {{ 1 }} ТЗ № 1
Установите соответствие м\у знакопеременными рядами видами сходимости
Абсолютно сходится 
Условно сходится 
Расходятся 
13. Задание {{ 1 }} ТЗ № 1
Сумма сходящегося числового ряда 
равна…
R 5
14. Задание {{ 1 }} ТЗ № 1
Сумма сходящегося числового ряда 
равна…
R 1.5
15. Задание {{ 1 }} ТЗ № 1
Сумма сходящегося числового ряда 
равна
R 30
Высокий уровень
16. Задание {{ 1 }} ТЗ № 1
Применив радикальный признак Коши (
) к ряду 
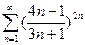, получаем…
R 
, ряд расходится
17. Задание {{ 1 }} ТЗ № 1
Радиус сходимости степенного ряда 
равен 10. Тогда интервал ходимости этого ряда имеет вид…
R (-9;11)
18. Задание {{ 1 }} ТЗ № 1
Применив радикальный признак Коши () к ряду 
, получаем…
R 
, ряд расходится
19. Задание {{ 1 }} ТЗ № 1
Радиус сходимости степенного ряда равен 12. Тогда интервал сходимости этого ряда имеет вид…
R (-11;13)
20. Задание {{ 1 }} ТЗ № 1
Радиус сходимости степенного ряда 
равен 10. Тогда интервал ходимости этого ряда имеет вид…
R (-8;2)
21. Задание {{ 1 }} ТЗ № 1
Применив радикальный признак Коши () к ряду 
, получаем…
R 
, ряд сходится
22. Задание {{ 1 }} ТЗ № 1
Найти коэффициент при 
в разложении функции 
в рядах Маклорена
R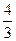 
23. Задание {{ 1 }} ТЗ № 1
Найти четыре первых члена в разложении в степенной ряд по степеням х функции 
R 
