Базовый уровень
Задние {{1}} ТЗ1
Укажите каноническое уравнение эллипса
R 
Задание {{1}} ТЗ1
Укажите каноническое уравнение гиперболы
R 
Задание {{1}} ТЗ1
Укажите каноническое уравнение параболы
R 
Задание {{1}} ТЗ1
Уравнение окружности радиуса R =3 с центром в точке С (–12) имеет вид
R (x +1)2+(y -2)2=9
Задание {{1}} ТЗ1
Уравнение эллипса, у которого большая полуось а =5, а малая полуось b =3 имеет вид
R 
Задание {{1}} ТЗ1
Уравнение эллипса, у которого большая полуось а =6, а малая полуось b =2 имеет вид
R 
Задание {{1}} ТЗ1
Геометрическое место точек, разность расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная, называется
R гиперболой
Задание {{1}} ТЗ1
Геометрическое место точек, сумма расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная, называется
R эллипсом
Задание {{1}} ТЗ1
Геометрическое место точек, равноотстоящих от данной точки, называемой фокусом, и данной прямой, называемой директрисой, есть
R парабола
Задание {{1}} ТЗ1
Дано уравнение окружности: 
. Ее радиус R и координаты центра С равны
R R=4, C(1-3)
Задание {{1}} ТЗ1
Уравнение гиперболы, у которой действительная полуось а =4, а мнимая полуось b =3, имеет вид
R 
Средний уровень
Задание {{1}} ТЗ1
Даны уравнения кривых:
1) 
: 2) 
: 3) 
: 4) 
.
Окружность описывают уравнения:
R 1,2
Задание {{1}} ТЗ1
Даны уравнения кривых:
1) 
2) 
3) 
4) 
.
Эллипс описывают уравнения:
R 2,4
Задание {{1}} ТЗ1
Даны уравнения кривых:
1) 
2) 
3) 
4) 
5) 
.
Гиперболу описывают уравнения:
R 2,3
Задание {{1}} ТЗ1
Дано уравнение гиперболы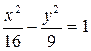 
.
Уравнения ее асимптот имеют вид:
R 
Задание {{1}} ТЗ1
Дано уравнение гиперболы 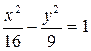. Координаты ее вершин (А 1 и А 2):
R А 1 (–40), А 2(40)
Задание {{1}} ТЗ1
Дана парабола 
. Координаты ее фокуса F и уравнение директрисы
R F (10), x = –1
Задание {{1}} ТЗ1
Уравнение окружности радиуса R =4 с центром в точке С (2 –3) имеет вид
R (x –2)2+(y +3)2 = 16
Задание {{1}} ТЗ1
Уравнение параболы, у которой фокус имеет координаты F (0,2), а директриса имеет уравнение x = –2, имеет вид
R y 2 = 8 x
Высокий уровень
Задание {{1}} ТЗ1
Расстояние между фокусами эллипса равно 6, а малая полуось b =4. Тогда уравнение этого эллипса имеет вид
R 
Задание {{1}} ТЗ1
Дано уравнение эллипса: 
. Координаты его фокусов:
R F 1(-40) F 2(40)
Задание {{1}} ТЗ1
Дана гипербола: . Координаты ее фокусов
R F 1(-50) F 2(50)
Задание {{1}} ТЗ1
Дано уравнение окружности: 
. Уравнение прямой, проходящей через ее центр параллельно прямой 
имеет вид
R 
Б- базовый (11)
С- средний (8)
Т- Высокий (4)
Тема 7. Прямая и плоскость в пространстве
Базовый уровень
Задание {{1}} ТЗ1
Канонические уравнения прямой линии в пространстве переменных x,y,z имеют вид:
R 
Задание {{1}} ТЗ1
Уравнение плоскости имеет вид: x –2 y +5 z –4=0. Вектор 
, перпендикулярный этой плоскости имеет координаты
R {1, –2,5}
Задание {{1}} ТЗ1
Направляющий вектор 
прямой линии, заданной каноническими уравнениями 
, имеет координаты
R 
Задание {{1}} ТЗ1
Дано уравнение плоскости: 
.
Вектор 
, перпендикулярный этой плоскости имеет координаты
R {1,2,–5}
Средний уровень
Задание {{1}} ТЗ1
Параметрические уравнения прямой линии в пространстве переменных x,y,z имеют вид:
R 
Задание {{1}} ТЗ1
Укажите уравнение плоскости, проходящей через данную точку 
перпендикулярно вектору .
R 
R 
.
Задание {{1}} ТЗ1
Расстояние от точки до плоскости 
, заданной уравнением 
, вычисляют по формуле
R 
Высокий уровень
Задание {{1}} ТЗ1
Каноническим уравнением прямой 
является уравнение
R 
Задание {{1}} ТЗ1
Уравнение плоскости, проходящей через точку М (1,2,0) перпендикулярно вектору 
,имеет вид
R 
Задание {{1}} ТЗ1
Даны две прямые: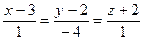 
и 
. Косинус угла между ними равен
R 
Б- базовый (4)
С- средний (3)
Т- Высокий (3)
Тема 8. Пределы
Базовый уровень
Задание {{1}} ТЗ1
Пусть функции 
и 
непрерывны и дифференцируемы в окрестности точки 
(кроме, быть может, точки ). В окрестности точки выполняются условия: 
, 
, существует предел 
. Тогда
R 
Задание {{1}} ТЗ1
Предел 
равен
R 1
Задание {{1}} ТЗ1
Предел 
равен
R 0
Задание {{1}} ТЗ1
Предел 
равен
R 1
Задание {{1}} ТЗ1
Предел 
равен
R 1
Задание {{1}} ТЗ1
Предел 
равен
R e
Задание {{1}} ТЗ1
Укажите первый замечательный предел.
R 
Средний уровень
Задание {{1}} ТЗ1
Предел 
равен:
R 
Задание {{1}} ТЗ1
Укажите второй замечательный предел.
R 
Задание {{1}} ТЗ1
Предел 
равен:
R 
Задание {{1}} ТЗ1
Предел 
равен:
R 
Задание {{1}} ТЗ1
Предел 
равен:
R 1
Задание {{1}} ТЗ1
Предел 
равен:
R 10
Задание {{1}} ТЗ1
Предел 
равен:
R -0,5
Задание {{1}} ТЗ1
Предел 
равен:
R 0
Задание {{1}} ТЗ1
Предел 
равен:
R ¥
Задание {{1}} ТЗ1
Предел 
равен:
R ¥
Задание {{1}} ТЗ1
Предел 
равен:
R 3
Задание {{1}} ТЗ1
Предел 
равен:
R 1/e
Задание {{1}} ТЗ1
Предел 
равен:
R 1
Задание {{1}} ТЗ1
Предел 
равен:
R e3
Задание {{1}} ТЗ1
Предел 
равен
R 0
Задание {{1}} ТЗ1
Предел 
равен
R 0
Задание {{1}} ТЗ1
Из перечисленных числовых последовательностей:
2) 
3) 
бесконечно малыми при n®¥ являются последовательности:
R 1, 3
Задание {{1}} ТЗ1
Из перечисленных функций: 1) sin2x 2) 3x 3) cosx 4) 2x эквивалентными при x ®0 являются следующие функции:
R 1, 4
Задание {{1}} ТЗ1
Из перечисленных функций 1) sinx 2) ln (1+ x) 3) x 4) cosx эквивалентными при x ®0 являются следующие функции
R 1, 2, 3
Высокий уровень
Задание {{1}} ТЗ1
Предел 
равен
R –1
Задание {{1}} ТЗ1
Предел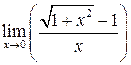 
равен
R 0
Задание {{1}} ТЗ1
Предел 
равен
R
Задание {{1}} ТЗ1
Предел равен
R 0
Задание {{1}} ТЗ1
Предел равен
R
Задание {{1}} ТЗ1
Предел 
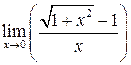равен
R 8/3
Задание {{1}} ТЗ1
Предел 
равен
R 6
Б- базовый (8)
С- средний (19)
Т- Высокий (5)
Тема 9. Производные функции f ( x )
Базовый уровень
Задание {{1}} ТЗ1
Угловой коэффициент нормали к графику функции y = f (x) в точке с абсциссой x 0 равен
R 
Задание {{1}} ТЗ1
Производная функции y = sin x – tg x имеет вид
R 
Задание {{1}} ТЗ1
Угловой коэффициент касательной к графику функции y = f(x) в точке с абсциссой x0 равен
R 
Задание {{1}} ТЗ1
Если 
и 
дифференцируемы в данной точке х, то производная их произведения находится по формуле:
R 
Задание {{1}} ТЗ1
Если и дифференцируемы в данной точке х, то производная их частного находится по формуле:
R 
Средний уровень
Задание {{1}} ТЗ1
Производная функции f (x) = 
имеет вид
R 
R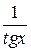 
Задание {{1}} ТЗ1
Производная функции f (x) = 
имеет вид
R 
Задание {{1}} ТЗ1
Производная функции f (x) = ln x – 3 x имеет вид
R 
Задание {{1}} ТЗ1
Производная функции f (x)=(x 3 × ex ) имеет вид
R 
Задание {{1}} ТЗ1
Производная функции f (x)= e x × sin x имеет вид
R 
Задание {{1}} ТЗ1
Производная функции f (x)= 
имеет вид
R 
Задание {{1}} ТЗ1
Производная функции f (x)= 
имеет вид
R 
Задание {{1}} ТЗ1
Производная функции f (x)= 
имеет вид
R 
Задание {{1}} ТЗ1
Производная функции f (x)= sin(x2+5x) имеет вид
R (2 x + 5) cos(x 2 + 5 x)
Задание {{1}} ТЗ1
Производная функции f (x)= esinx имеет вид
R e sin x × cos Xj
Задание {{1}} ТЗ1
Производная функции f (x)= ln(3 x –7) имеет вид
R 
Задание {{1}} ТЗ1
Производная функции f (x)=sin(x 2 + 2) имеет вид
R cos(x 2 + 2) ×2 х
Задание {{1}} ТЗ1
Производная функции f (x)=2 x 3–5 при x 0=3 равна
R 54
Высокий уровень
Задание {{1}} ТЗ1
Производная функции f (x)= 
имеет вид
R 
Задание {{1}} ТЗ1
Производная функции f (x)= 
равна
R 
Задание {{1}} ТЗ1
Дана функция f (x)= 
. Если аргументу х 0 дано приращение D х, то приращение D f функции f (x) равно
R 10 x 0 × D х + 5(D х)2
Задание {{1}} ТЗ1
Дана функция f (x)= x 3. Если аргументу х 0 дано приращение D х, то приращение D f функции f (x) равно
R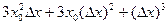 
Задание {{1}} ТЗ1
Уравнение касательной к кривой y = x 2 в точке M (2,4) имеет вид
R y = 4 x - 4
Задание {{1}} ТЗ1
Уравнение нормали к кривой y = x 2 в точке M 0(2 4) имеет вид
R 
Задание {{1}} ТЗ1
Угловой коэффициент нормали к кривой y =sin x в точке 
равен
R 
Задание {{1}} ТЗ1
Угловой коэффициент касательной к кривой 
в точке 
равен
R 1
Задание {{1}} ТЗ1
Угловой коэффициент нормали к кривой y =e2 x в точке M 0(0, 1) равен
R –1/2
Задание {{1}} ТЗ1
Функция y = ½ x ½ в точке x = 0
R не имеет производную
Б- базовый (5)
С- средний (13)
Т- Высокий (10)
