Легкий
Задание {{1}} ТЗ1
Функция 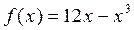
R имеет две стационарные точки 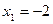 и
и 
Задание {{1}} ТЗ1
Функция 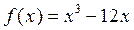
R имеет две стационарные точки 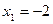 и
и 
Задание {{1}} ТЗ1
Функция 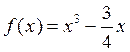
R имеет две стационарные точки 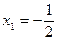 и
и 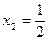
Средний
Задание {{1}} ТЗ1
Функция 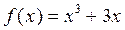
R имеет две стационарные точки 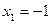 и
и 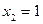
Задание {{1}} ТЗ1
Функция 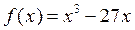
R имеет две стационарные точки 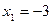 и
и 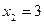
Задание {{1}} ТЗ1
Функция 
R имеет две стационарные точки 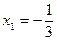 и
и 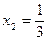
Задание {{1}} ТЗ1
Функция 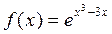
R имеет две стационарные точки 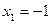 и
и 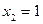
Тредный
Задание {{1}} ТЗ1
Функция 
R не имеет стационарных точек
Задание {{1}} ТЗ1
Функция 
R имеет две стационарные точки 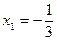 и
и 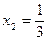
Задание {{1}} ТЗ1
Функция 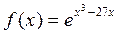
R имеет две стационарные точки 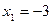 и
и 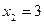
Тема 11. Локальный экстремум функции f(x)
Легкий
Задание {{1}} ТЗ1
Функция 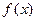 определена на отрезке [1,3], при этом:
определена на отрезке [1,3], при этом: 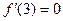 ,
, 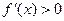 для
для  . Тогда
. Тогда
R  монотонно возрастает в интервале
монотонно возрастает в интервале 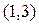
213. Задание {{1}} ТЗ1
Функция 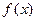 определена на отрезке [ –2,4], при этом:
определена на отрезке [ –2,4], при этом: 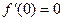 ,
, 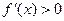 для
для 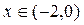 ,
, 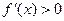 для
для 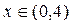 . Тогда
. Тогда
R 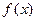 возрастает в интервале
возрастает в интервале 
Задание {{1}} ТЗ1
Функция 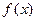 определена на отрезке [–2,2], при этом:
определена на отрезке [–2,2], при этом:  ,
, 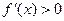 для
для 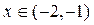 ,
,  для
для 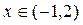 . Тогда
. Тогда
R 
Средний
Задание {{1}} ТЗ1
Функция 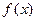 определена на отрезке [2,5], при этом:
определена на отрезке [2,5], при этом: 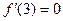 ,
,  для
для  ,
,  для
для  . Тогда
. Тогда
R 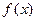 не имеет локального экстремума в интервале
не имеет локального экстремума в интервале 
Задание {{1}} ТЗ1
Функция 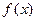 определена на отрезке [1,7], при этом:
определена на отрезке [1,7], при этом: 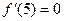 ,
,  для
для 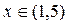 ,
, 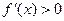 для
для 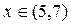 . Тогда
. Тогда
R 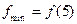
Задание {{1}} ТЗ1
Функция 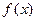 определена на отрезке [–2,1], при этом:
определена на отрезке [–2,1], при этом: 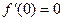 ,
, 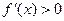 для
для 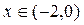 ,
,  для
для 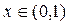 . Тогда
. Тогда
R 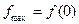
Трудный
Задание {{1}} ТЗ1
Функция 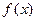 определена на отрезке [2,7], при этом:
определена на отрезке [2,7], при этом: 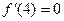 ,
, 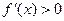 для
для  ,
, 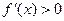 для
для 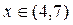 . Тогда
. Тогда
R 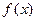 возрасает в интервале
возрасает в интервале 
Задание {{1}} ТЗ1
Функция 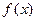 определена на отрезке [–1,2], при этом:
определена на отрезке [–1,2], при этом: 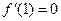 ,
,  для
для  ,
, 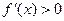 для
для  . Тогда
. Тогда
R 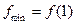
Задание {{1}} ТЗ1
Функция 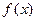 определена на отрезке [1,4], при этом:
определена на отрезке [1,4], при этом: 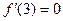 ,
,  для
для  ,
,  для
для 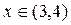 . Тогда
. Тогда
R 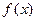 не имеет локального экстремума в интервале
не имеет локального экстремума в интервале 
Задание {{1}} ТЗ1
Функция 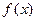 определена на отрезке [–2,6], при этом:
определена на отрезке [–2,6], при этом:  ,
,  для
для  . Тогда
. Тогда
R 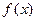 не имеет локального экстремума в интервале
не имеет локального экстремума в интервале 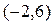
Интегралы.
Базовый уровень
1. Задание {{ 1 }} ТЗ № 1
Укажите теорему интегрирования по частям в определенном интеграле, если 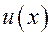 ,
,  ,
, 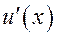 ,
, 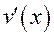 непрерывны на
непрерывны на  :
:
R 
2. Задание {{ 1 }} ТЗ № 1
Укажите формулу Ньютона-Лейбница:
R 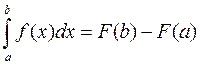
3. Задание {{ 1 }} ТЗ № 1
Функция F определенная на некотором промежутке называется первообразной функции 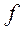 , если:
, если:
R 
4. Задание {{ 1 }} ТЗ № 1
Функция, производная которой равна f(x) или дифференциал которой равен выражению f(x)dx, называется
R первообразной
5. Задание {{ 1 }} ТЗ № 1
Интеграл функции y = -3sinx равен
R 3cosx + C
6. Задание {{ 1 }} ТЗ № 1
Интеграл функции y = 2/cos2x равен
R 2tgx + C
7. Задание {{ 1 }} ТЗ № 1
Интеграл функции 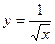 равен
равен
R 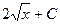
8. Задание {{ 1 }} ТЗ № 1
Если функция f(x) непрерывна на сегменте [a,b]; F(x) – одна из ее первообразных, то справедлива формула 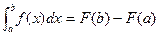 , то есть определенный интеграл равен приращению первообразной от подынтегральной функции на промежутке интегрирования – эта теорема
, то есть определенный интеграл равен приращению первообразной от подынтегральной функции на промежутке интегрирования – эта теорема
R Ньютона-Лейбница
Средний уровень
9. Задание {{ 720 }} ТЗ № 20
Интеграл 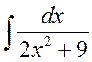 равен:
равен:
R 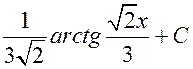
10. Задание {{ 720 }} ТЗ № 20
Интеграл  равен:
равен:
R 
11. Задание {{ 1 }} ТЗ № 1
Интеграл функции y = 2x2 – 2x – 7 равен
R (2/3)x3 – x2 – 7x + C
12. Задание {{ 1 }} ТЗ № 1
Интеграл функции 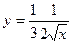 равен
равен
R 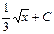
13. Задание {{ 1 }} ТЗ № 1
Интеграл функции 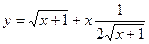 равен
равен
R 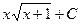
14. Задание {{ 1 }} ТЗ № 1
Интеграл функции 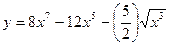 равен
равен
R 
15. Задание {{ 1 }} ТЗ № 1
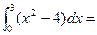
R –3
16. Задание {{ 1 }} ТЗ № 1
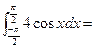
R 8
17. Задание {{ 1 }} ТЗ № 1
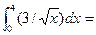
R 12
18. Задание {{ 1 }} ТЗ № 1
В неопределенном интеграле
 введена новая переменная
введена новая переменная
t=3+cos5x тогда интеграл приметет вид…
R 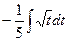
19. Задание {{ 1 }} ТЗ № 1
В неопределенном интеграле 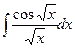 введена новая переменная t=
введена новая переменная t= 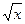 . Тогда интервал примет вид…
. Тогда интервал примет вид…
R 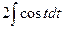
20. Задание {{ 1 }} ТЗ № 1
Какова площадь фигуры, ограниченный осью Ох и графиком функции 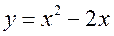 при
при 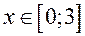
R 
21. Задание {{ 1 }} ТЗ № 1
Определенный интеграл 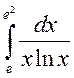 равен:
равен:
R 
22. Задание {{ 720 }} ТЗ № 20
Интеграл  равен:
равен:
R 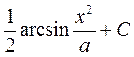
23. Задание {{ 1 }} ТЗ № 1

R 0
24. Задание {{ 1 }} ТЗ № 1
Площадь фигуры, ограниченной линиями y-x2=0, y2-x=0 на отрезке [0;1] равна
R 1/3
25. Задание {{ 1 }} ТЗ № 1
Площадь фигуры, ограниченной линиями y-x2=0 и y2+x=0 на отрезке [-1;0] равна
R 1/3
26. Задание {{ 1 }} ТЗ № 1
Площадь фигуры, ограниченной линиями y = (1-x); y = 4, x=1, х= 0 равна
R 7/2
27. Задание {{ 1 }} ТЗ № 1
Площадь фигуры, ограниченной линиями y = (x+1); y = 4, x = 0 и х=1 равна
R 5/2
28. Задание {{ 1 }} ТЗ № 1
Определенный интеграл 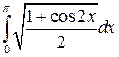 равен:
равен:
R 0.
29. Задание {{ 1 }} ТЗ № 1
Определенный интеграл  равен…
равен…
R 1
30. Задание {{ 1 }} ТЗ № 1
Несобственный интеграл 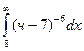 равен…
равен…
R 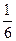
31. Задание {{ 1 }} ТЗ № 1
Несобтвенный интеграл 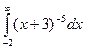 равен…
равен…
R 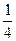
32. Задание {{ 1 }} ТЗ № 1
Определенный интеграл 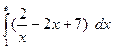 равен…
равен…
R 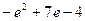
33. Задание {{ 1 }} ТЗ № 1
Определенный интеграл 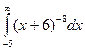 равен…
равен…



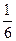
Функции нескольких переменных
Базовый уровень
1) Задание {{1}} ТЗ № 1
Частной производной функции z=f(x,y)  по переменной x называется…
по переменной x называется…
R производная по переменной x при построенном y
R предел отношения приращения функции по переменной x к приращению этой переменной, когда последнее стремиться к нулю
2) Задание {{1}} ТЗ № 1
Полным дифференциалом функции z=f(x,y) в точке (x  ,y
,y  ) является…
) является…
R главная часть полного приращения функции в точке (x  ,y
,y  ), линейная относительно
), линейная относительно 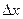 и
и 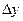
R f  (x
(x  ,y
,y  )
) 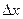 + f
+ f 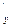 (x
(x  ,y
,y  )
) 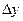
3) Задание {{1}} ТЗ № 1Формула для приближенного вычисления значения функции z=f(x,y) в точке (x  +
+ 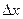 ,y
,y  +
+ 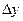 ) имеет вид…
) имеет вид…
R f(x  +
+ 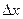 ,y
,y  +
+ 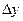 )≈f(x
)≈f(x  ,y
,y  )+df(x
)+df(x  ,y
,y  )
)
R f(x  +
+ 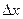 ,y
,y  +
+ 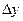 )≈f(x
)≈f(x  ,y
,y  )+ f
)+ f 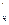 (x
(x  ,y
,y  )
) 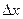 + f
+ f 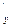 (x
(x  ,y
,y  )
) 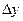
4) Задание {{1}} ТЗ № 1
Градиентом функции z=f(x,y) в точке (x  ,y
,y  ) называеться
) называеться
R вектор на плоскости XOY, задающий направление, в котором скорость изменения функции наибольшая
R вектор координатами которого является частные производные функции в точке (x  ,y
,y  )
)
5) Задание {{1}} ТЗ № 1
Производной функции z=f(x,y) в точке (x  ,y
,y  ) по направлению
) по направлению 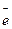 (|e|cosα, |e|cosβ) являются…
(|e|cosα, |e|cosβ) являются…
R число f 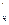 (x
(x  ,y
,y  ) cosα + f
) cosα + f 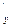 (x
(x  ,y
,y  )cosβ
)cosβ
6) Задание {{1}} ТЗ № 1
Частной производной функции z=f(x,y) по переменной y называется…
R производная по переменной y при постоянном x
R предел отношения прирощения функции по переменной у к прирощению этой переменной, когда последнее стремиться к нулю
7) Задание {{1}} ТЗ № 1
Полным дифференциалом функции n=f(x,y,z) в точке (x  ,y
,y  ,z
,z  ) является…
) является…
R главная часть приращения функции в точке (x  ,y
,y  ,z
,z  ), линейна относительно
), линейна относительно 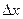 ,
, 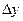 ,
, 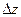 .
.
R f  (x
(x  ,y
,y  ,z
,z  )
) 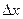 +f
+f 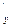 (x
(x  ,y
,y  ,z
,z  )
) 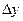 +f
+f  (x
(x  ,y
,y  ,z
,z  )
) 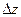 .
.
8) Задание {{1}} ТЗ № 1
Градиентом функции n=f(x,y,z) в точке (x  ,y
,y  ,z
,z  ) назаваеться…
) назаваеться…
R вектор (f  (x
(x  ,y
,y  ,z
,z  ),f
),f 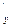 (x
(x  ,y
,y  ,z
,z  ),f
),f  (x
(x  ,y
,y  ,z
,z  ))
))
R вектор, координатами которого являются чачтные производные функции в точке (x  ,y
,y  ,z
,z  )
)
9) Задание {{1}} ТЗ № 1
Линией уровня с функцией z=f(x,y) называеться…
R линия на плоскости XOY, во всех точках которой функция принимает значение с
R линия, имеющая уравнение γ(x,y)=0, такое что из γ(x  ,y
,y  )=0 следует f(x
)=0 следует f(x  ,y
,y  )=C.
)=C.
10) Задание {{1}} ТЗ № 1
Указать линию уровня 5 функции z=ln y =0
R x ln y =0
11) Задание {{1}} ТЗ № 1
Указать линию уровня c функции z=e  y
y 
R e  y
y  =c
=c
Средний уровень.
12) Задание {{1}} ТЗ № 1
Частная производная функции 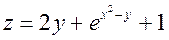 по переменной
по переменной 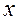 равна:
равна:
R 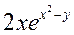
13) Задание {{1}} ТЗ № 1
Частная производная функции  по переменной
по переменной 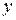 равна:
равна:
R 
14) Задание {{1}} ТЗ № 1
Частная производная функции 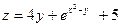 по переменной
по переменной 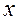 равна:
равна:
R 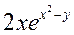
15) Задание {{1}} ТЗ № 1
Частная производная функции 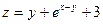 по переменной y равна
по переменной y равна
R 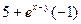
16) Задание {{1}} ТЗ № 1
Частная производная функции  по переменной X равна
по переменной X равна
R 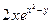
17) Задание {{1}} ТЗ № 1
Частная производная функции 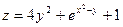 по переменной y равна
по переменной y равна
R 
18) Задание {{1}} ТЗ № 1
Частная производная функции  по переменной X равна
по переменной X равна
R 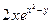 +1
+1
19) Задание {{1}} ТЗ № 1
Частная производная функции  по переменной y равна
по переменной y равна
R 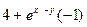 +x
+x
20) Задание {{1}} ТЗ № 1
Частная производная функции 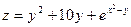 по переменной X равна
по переменной X равна
R 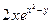
21) Задание {{1}} ТЗ № 1
Частная производная функции 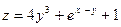 по переменной y равна
по переменной y равна
R 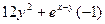
22) Задание {{1}} ТЗ № 1
Частная производная функции  по переменной X равна
по переменной X равна
R 
Высокий уровень
23) Задание {{1}} ТЗ № 1
Максимум функции z=xy при условии x+y=2 равен
R 1
24) Задание {{1}} ТЗ № 1
Максимум функции z=xy при условии x+y=3 равен
R 2.25
25) Задание {{1}} ТЗ № 1
Максимум функции z=xy при условии x+y=5 равен
R 6.25
26) Задание {{1}} ТЗ № 1
Максимум функции z=xy при условии x+y=7 равен
R 12.25






