1. 
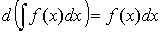; 2. 
3. 
;
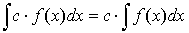4. 
.
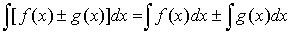19.Табличное интегрирование.
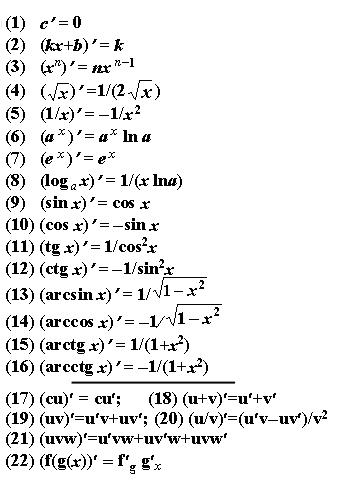
20. Метод замены переменной интегрирования.
Вычислить интегралы методом замены переменой:
Здесь 1/(1+x²) — производная от функции arctg x. Поэтому в качестве новой переменной t возьмем arctg x. Далее — воспользуемся таблицей интегралов:
После того, как нашли интеграл от t, выполняем обратную замену:
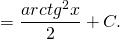
21. Метод интегрирования по частям.
Это способ вычисления неопределенного интеграла, основанный на соотношении
(*)
где u (x) и v (x) – непрерывно дифференцируемые функции, d (u (x)) и d (v (x)) – их дифференциалы.
Для вычисления определенного интеграла справедлива аналогичная формула; разница, естественно, в том, что окончание вычисления здесь – применение формулы Ньютона-Лейбница, и выбор технической детали – пересчитывать ли пределы интегрирования при замене переменной или сначала вычислить неопределенный интеграл, а затем применить формулу Ньютона-Лейбница с пределами изменения исходной переменной. Приведём эту формулу:
. (**)
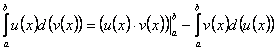22. Интегрирование рациональных дробей.
Рациональной дробью называется выражение вида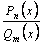 
, где 
, 
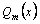–многочлены степеней n и m соответственно.
Если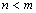 
, рациональная дробь называется правильной, в противном случае 
– неправильной.
Если дробь неправильная, из нее можно выделить целую часть, разделив числитель на знаменатель.
Например, 
–неправильная рациональная дробь. Выполним деление:
| 
| 
| ||
| 
| |||
| 
| |||
| ||||
| 
| |||
| 
| |||
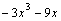
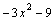
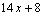
| остаток |
Таким образом, неправильную дробь можно представить в виде суммы целой рациональной функции (многочлена) и правильной дроби:
.
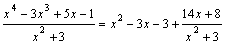Простейшими рациональными дробями называются правильные рациональные дроби следующих четырех типов:
| 
| 
|  ,
|
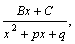
где A, B, C, a, p, q –числа, 
Покажем на примерах, как интегрируются дроби каждого типа.
Дробь 1–го типа: 
Дробь 2–го типа:
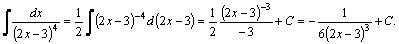
Дробь 3–го типа: 
=[выделим в знаменателе полный квадрат и введем новую переменную: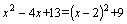 
; 
]= 
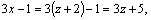
=[разобьем интеграл на сумму двух интегралов, первый из которых вычислим подведением под знак дифференциала, второй–табличный]=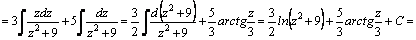 
23. Определение и свойства определенного интеграла.
Определение: Функция 
называется интегрируемой на отрезке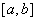 
, если существует конечный предел её интегнральных сумм на 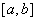. Обозначается: 
.
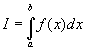Свойства:
1. Если с — постоянное число и функция ƒ(х) интегрируема на [a;b], то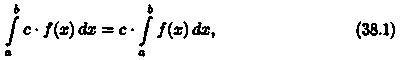 
2. Если функции ƒ1(х) и ƒ2(х) интегрируемы на [а;b], тогда интегрируема на [а; b] их сумма u
3. 
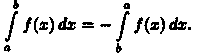
4. Если функция ƒ(х) интегрируема на [а; b] и а < с < b, то
24. Способы вычисления определенного интеграла.
1) 
2) Интегрирование заменой переменной.
3) Интегрирование по частям.
