Билет. Понятие предела функции в точке и на бесконечности.
Определение предела по Коши. Число A называется пределом функции f (x) в точке a, если эта функция определена в некоторой окрестности точки a за исключением, быть может, самой точки a, и для каждого ε > 0 существует δ > 0 такое, что для всех x, удовлетворяющих условию |x – a| < δ, x ≠ a, выполняется неравенство |f (x) – A| < ε.
Определение предела по Гейне. Число A называется пределом функции f (x) в точке a, если эта функция определена в некоторой окрестности точки a за исключением, быть может, самой точки a, и для любой последовательности такой, что сходящейся к числу a, соответствующая последовательность значений функции сходится к числу A.
Докажем
Билет. Арифметические свойства пределов.
Оператор взятия предела числовой последовательности является линейным, т. е. проявляет два свойства линейных отображений
Аддитивность. Предел суммы числовых последовательностей есть сумма их пределов, если каждый из них существует.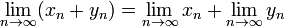 
Однородность. Константу можно выносить из-под знака предела
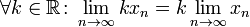
Предел произведения числовых последовательностей факторизуется на произведение пределов, если каждый из них существует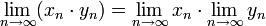 
Предел отношения числовых последовательностей есть отношение их пределов, если эти пределы существуют и последовательность-делитель не является бесконечно малой
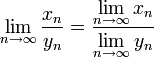
Билет 5 Основные неопределенности и приемы их раскрытия.
Раскрытие неопределённостей — методы вычисления пределов функций, заданных формулами, которые в результате формальной подстановки в них предельных значений аргумента теряют смысл, то есть переходят в выражения типа:
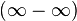
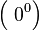
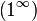
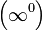
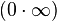
Все другие выражения не являются неопределенностями и принимают какое-то конкретное конечное или бесконечное значение.
Раскрытие неопределенностей
Для раскрытия неопределенностей используют следующее:
1. упрощают выражение функции: раскладывают на множители, преобразовывают функцию с помощью формул
сокращенного умножения, тригонометрических формул, домножают на сопряженное, что позволяет в дальнейшем сократить и т.д., и т.п.;
2. замечательные пределы - первый замечательный предел и второй замечательный предел;
3. правило Лопиталя;
4. эквивалентные бесконечно малые функции.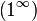
Билет 6 Замечательные пределы.
Так называют следующие равенства:
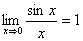– первый замечательный предел; 
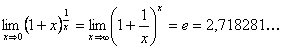второй замечательный предел.
Они замечательны тем, что помогают вычислению многих других пределов.
Так, с помощью первого замечательного предела можно установить важную для приложений эквивалентность при стремлении х к нулю следующих бесконечно малых величин: ax, sinax, tgax, arcsinax, arctgax(эквивалентность означает, что их отношение стремится к 1 при стремлении х к нулю). Отметим, что аргументы тригонометрических и обратных тригонометрических функций здесь измеряются в радианах, как это обычно бывает при рассмотрении подобных функций.
Среди непосредственных следствий второго замечательного предела можно указать такие: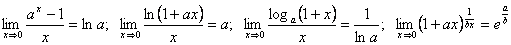 
В теории пределов так называется каждое из трех равенств:
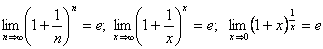
где е = 2,71828… – как доказано в 1873 г. французским математиком Ш. Эрмитом, трансцендентное число, основание натуральных логарифмов, говорят также неперово число (названо в честь шотландского математика Непера; как считают многие современные исследователи, необоснованно).
