1. Что понимается под законом распределения?
2. Какие знаете законы распределения?
3. Что такое функция распределения, какими свойствами она обладает?
4. Что такое плотность распределения, какими свойствами она обладает?
5. Какое распределение называют нормальным (нормированным, равномерным)?
6. Опишите распределение Стьюдента, Фишера, «хи-квадрат».
Задача 1
Текущая цена акции может быть приблизительно смоделирована при помощи нормального распределения с математическим ожиданием 15,28 тенге и средним квадратическим отклонением, равным 0,12 тенге. Рассчитайте вероятность того, что цена:
а) не ниже 15,5;
б) между 15,1 и15,4
в) не выше 15,0.
Методические рекомендации:
Используйте функцию Лапласа.
Задача 2
Цена акции нормально распределена. В течение последнего года на протяжении 20% рабочих дней цена была ниже 20 у.е. В 75% случаев цена была выше 25 у. е. Найти математическое ожидание и среднее квадратическое отклонение цены акции.
Методические рекомендации:
1.Найти вероятности того, что случайная величина меньше 20 и больше 25.
2 Воспользовавшись функцией Лапласа составить систему уравнений
3. Решить систему уравнения, найти ее параметры.
Задача 3
Дискретная случайная величина задана законом распределения:
а)
| х | |||
| р | 0,2 | 0,1 | 0,7 |
б)
| х | -1 | ||
| р | 0,1 | 0,2 | 0,7 |
Найти закон распределения случайной величины Х = У4.
Методические рекомендации:
Найти все возможные значения Х и их вероятности.
Задача 4
Независимые дискретные случайные величины заданы следующими законами распределения:
Статистические оценки распределения вероятностей
| х | у | |||||
| р | 0,3 | 0,5 | 0,2 | р | 0,2 | 0,8 |
Найти законы распределения функций:
а) Z = Y +X
б) Z = XY
Методически рекомендации:
Найти все возможные значения Z и их вероятности, используя свойства вероятностей.
Основная литература: [6], [5], [11], [12]
Дополнительная литература: [22]
Тема № 3 (занятие 4) Статистические оценки распределения
1. В чем отличие точечной и интервальной оценок?
2. Когда предпочтительнее использование интервальной оценки перед точечной?
3. Что такое доверительная вероятность и уровень значимости?
4. Какую оценку можно считать несмещенной (состоятельной, эффективной)?
5. Как связана ширина доверительного интервала и доверительная вероятность?
Задача1
С целью определения средней суммы вкладов в банке, имеющем 2 200 вкладчиков, проведено выборочное обследование (бесповторная выборка) вкладов, результаты которого даны в таблице
| Сумма вкладов, тыс. у. е. | 10 – 30 | 30 – 50 | 50 – 70 | 70 – 90 | 90 – 110 | 110 – 130 |
| Число вкладов |
Необходимо найти доверительные границы для генерального среднего, которые можно было бы гарантировать с вероятностью 0,96.
Методические рекомендации:
Сначала находим выборочное среднее 
и выборочную дисперсию s2, для чего, в качестве значения признака Х берем середины интервалов: Х 1 = = 20; Х 2 = 40; Х 3 = 60; Х 4 = 80; Х 5 = 100; Х 6 = 120.
1.Тогда 
89,91. Проведите подробный расчет.
2. s2 = 330,64. Проведите подробный расчет.
3. Вычисляем среднюю ошибку выборки:
=1,69
Так как по условию 2 Ф0(t) = 0,96,® Ф0(t)=0,48 то по таблице функции Лапласа из приложение1 имеем t =?. Таким образом, предельная погрешность ê = t•m, а доверительными границами для генерального среднего будут
. Проведите подробный расчет.
Задача 2
Выборка из 25 наблюдений за доходами по индексу цен характеризуется средней 0,005 и средним квадратическим отклонением 0,02. Предположив, что недельные доходы нормально распределены, рассчитайте 95 %-ный доверительный интервал для средней доходности.
Методические рекомендации:
1. Найти по таблице критическое значение для двусторонней проверки.
2. Найти точность оценки, затем и доверительный интервал.
Задача 3
Рассчитайте стандартную ошибку средней по отношению к доходу по финансовому индексу со средним значением в 10 % и средним квадратическим значением 16% на основе 60 наблюдений. Рассчитайте 95 %-ный доверительный интервал для выборочной средней и выборочного среднего квадратического отклонения.
Методические рекомендации:
1.Найти ошибку выборки.
2.В соответствии с критическим значением найти доверительный интервал для математического ожидания нормального распределения при известном среднем квадратическом отклонении.
3. В соответствии с критическим значением найти доверительный интервал для среднего квадратического отклонения нормального распределения.
Задача 4
Известны исправленное среднее отклонение, выборочная средняя и объем малой выборки нормального распределения признака. Найти, пользуясь распределением Стьюдента, доверительные интервалы для оценки математического ожидания с заданной надежностью.
а) s = 1,5 xb = 16,8 n = 12 γ = 0,95
б) s = 2,4 xb = 14,2 n =9 γ = 0,99
Основная литература: [6], [5], [11], [12]
Дополнительная литература: [22]
Тема № 5 (занятие 5) Проверка гипотез
1. Что понимается под статистической гипотезой?
2. Какие виды гипотез вы знаете?
3. Что понимается под ошибкой первого рода (второго рода)?
4. Правило приятия решения, критическая область, ОДЗ, критические точки
5. Каков алгоритм проверки гипотез?
6. Правосторонняя (левосторонняя, двусторонняя) проверка гипотезы
7. Сравнение средней, дисперсии, форм распределения.
Задача1
Компания заявила, что месячный доход по ее высокодоходному инвестиционному фонду превысил доход индекса на 0,3% или на 0,003. В течение одногодичного периода средний доход по индексу составил 0,005, а средний доход фонда – 0,0065, среднее квадратическое отклонение равно 0,019. Выполните одностороннюю статистическую проверку, чтобы выяснить, насколько верно заявление компании.
Задача 2
Компания заявила, что месячный доход по ее высокодоходному инвестиционному фонду превысил доход индекса на 0,3% или на 0,003. В течение одногодичного периода средний доход по индексу составил 0,005, а средний доход фонда – 0,0065, среднее квадратическое отклонение равно 0,019. Выполните одностороннюю статистическую проверку гипотезы, что доход по портфелю фактически превысил доход по индексу.
Задача 3
Управляющий портфелем заботиться о том, чтобы не осуществлять инвестиционные вложения в ценные бумаги с дисперсией годовой доходности более чем 0,04. Выборка из 52 наблюдений за доходом по активу «А» показала, что дисперсия равна 0,045. Проверьте гипотезу, что доход по активу «А» характеризуется дисперсией меньшей или равной 0,04.
Задача 4
Владелец фирмы считает, что добиться более высоких финансовых результатов ему помешала неравномерность поставок комплектующих по месяцам года, несмотря на то, что поставщик в полном объеме выполнил свои обязательства за год. Поставщик утверждает, что поставки были не так уж неравномерны. Распределение поставок по месяцам года имеет следующий вид:
| Месяц | ||||||||||||
| Объем поставок, единиц |
На уровне значимости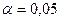 
определите, кто прав: владелец фирмы или поставщик? Изменится ли ответ на поставленный вопрос, если уровень значимости принять равным 0,01? Объясните результаты.
Задача5
Главный бухгалтер большой корпорации провел обследование по данным прошедшего года с целью выяснения доли некорректных счетов. Из 2000 выбранных счетов в 25 оказались некорректные проводки. Для уменьшения доли ошибок он внедрил новую систему. Год спустя он решил проверить, как работает новая система, и выбрал для проверки в порядке случайного отбора 3000 счетов компании. Среди них оказалось 30 некорректных. Можем ли мы утверждать, что новая система позволила уменьшить долю некорректных проводок в счетах? Принять уровень значимости .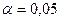
Основная литература: [5-14]
Дополнительная литература: [20] [32]
Тема № 6 (занятие 6- 7) Парный линейный и нелинейный регрессионный анализ
1. В чем состоят ошибки спецификации модели?
2. Поясните смысл коэффициента регрессии, назовите способы его оценивания.
3. Какие допущения Гаусса-Маркова вы знаете?
4. Какова концепция F-критерия Фишера?
5. Какие формы связи вы знаете?
6. Когда оценки называются наилучшие линейные несмещенные?
7. Какие статистические тесты вам известны, в чем их смысл?
Задача 1
Изучается зависимость материалоемкости продукции от размера предприятия по 10 однородным предприятиям:
| показатель | Материалоемкость продукции по предприятиям | |||||||||
| Потребление материалов на единицу продукции, кг | 3,7 | 3,6 | 3,5 | 3,5 | ||||||
| Выпуск продукции, тыс. ед. |
Задание
1. Найдите параметры уравнения yi(x) =a + b/xi.
2. Оцените тесноту связи с помощью коэффициента корреляции.
3. Охарактеризуйте эластичность изменения материалоемкости продукции.
4. Сделайте вывод о значимости уравнения регрессии.
Методические рекомендации.
1.Уравнение равносторонней гиперболы yi(x) =a + b/x линеаризуется при замене Z=1/x. Тогда yi(z)=a+bzi. Коэффициенты a,b находим стандартным образом.
2. Коэффициент корреляции вычислим по формуле:
3. Коэффициент эластичности показывает на сколько % в среднем изменится результативный признак У при изменении на 1% факторного признака Х.
4. Оценивание качества уравнения регрессии - состоит в проверке гипотезы Ho о статистической незначимости уравнения регрессии и показателя тесноты связи. Тест сводится к сравнению двух чисел Fфакт Fкрит. Если Fфакт > Fкрит, то Ho отклоняется и признается значимость и надежность уравнения регрессии.
Fкрит=Fa;m;n-m-1 находится по критическим точкам распределения Фишера. Приложение3.
Задача 2
По 20 регионам страны изучается зависимость уровня безработицы у (%) от индекса потребительских цен х (% к предыдущему году). Информация о логарифмах исходных показателей представлена в таблице:
| показатель | ln x | ln y |
| Среднее значение | 0,6 | 1,0 |
| Среднее квадратическое отклонение | 0,4 | 0,2 |
Известно также, что коэффициент корреляции между логарифмами исходных показателей составил rlnxlny = 0,8.
Задание
1. Постройте уравнение регрессии зависимости уровня безработицы от индекса потребительских цен в степенной форме.
2. Дайте интерпретацию коэффициента эластичности данной модели регрессии.
3. Определите значение коэффициента детерминации и поясните его смысл.
Методические рекомендации.
1. Уравнение прямой парной регрессии имеет вид: 
. После подсчета коэффициентов выполнить потенцирование.
2. Вычисление коэффициента эластичности и проверки значимости уравнения, смотри пример1.
Задача 3
Для двух видов продукции А и Б зависимость расходов предприятия у (тысяч тенге) от объемов производства х (штук) характеризуется данными, представленными в таблице:
| Уравнение регрессии | Показатели корреляции | Число наблюдений |
| уА = 160+0,8 х | 0,85 | |
| уБ = 50х0,6 | 0,72 |
Задание
1. Поясните смысл величин 0,8 и 0,6 в уравнениях регрессии.
2. Сравните эластичность расходов от объема производства для продукции А и Б при выпуске продукции А в 500 единиц.
3. Оцените значимость каждого уравнения регрессии с помощью F - критерия Фишера.
Методические рекомендации. Смотри пример1.
Основная литература: [5], [7], [11], [12-14]
Дополнительная литература: [20] [32]
Тема № 9 (занятие 8) Изучение взаимосвязей непараметрическими методами
1. Чтопонимается под ранговой корреляцией?
2. Какие вы знаете методы ранговой корреляции?
3. Как рассчитываются ранговые коэффициенты корреляции?
4. Назовите свойства ранговых коэффициентов корреляции Кендалла и Спирмена, коэффициента конкордации.
5. Когда необходимо использовать измерители тесноты ранговой связи?
Задача 1
Пусть имеется 5 продуктов, расположенных по порядку предпочтений от 1 до 5 в соответствии с 2 характеристиками X и Y.
Задание
1. Вычислить степень тесноты парной связи между ранговыми оценками характеристик с помощью рангового коэффициента корреляции Спирмена.
2. Проверить значимость коэффициента Спирмена.
| Характеристики для ранжирования | Продукт | ||||
| А | Б | С | Г | Д | |
| X | |||||
| Y |
Методические рекомендации
1.Наличие взаимосвязи между ранговыми оценками проверяется с помощью коэффициента Спирмена.
где n –число пар ранжированных наблюдений. D2=РангХ –рангУ.
В нашем случае n=5. SD2=(2-1)2+(5-3)2+…+(4-5)2=8
2. Значимость коэффициента Спирмена проверяется на основе t – критерия Стьюдента по формуле
, значение коэффициента считается существенным, если tнабл>tкрит(a;n-2).
Критические tкрит(a;n-2) находятся по таблице приложения 2. Проведите полные выкладки.
Задача 2
Зависимость между средними ежемесячными доходами семьи X (тысяч тенге), накоплениями Y (сбережения в банках, тысяч тенге) и ежемесячными расходами Z (тысяч тенге) представлена в таблице:
| X | 7,2 | 7,2 | 9,1 | 9,6 | 7,3 | 3,0 | 6,3 | 2,3 | 6,6 | 10,3 |
| Y | ||||||||||
| Z | 4,2 | 4,5 | 5,7 | 5,6 | 4,6 | 2,1 | 4,2 | 1,7 | 4,1 | 5,8 |
Задание
1. Вычислите парные ранговые коэффициенты Кендалла и Спирмена.
2. Проверьте гипотезу о значимости множественной ранговой связи между всеми компонентами.
3. Сделайте выводы
Задача 3
Найти выборочный коэффициент ранговой корреляции Спирмена по данным рангам объектов выборки объема n = 10.
| х | ||||||||||
| у |
Значима ли ранговая корреляционная связь при уровне значимости 0,05.
Методические рекомендации. Смотри задачу 1.
Основная литература: [5, С.281-343], [7, С.73-114], [11, С.34-54.], [12,С.65-79],[13] [14]
Дополнительная литература: [20] [32]
Тема № 10 (занятие 9-13) Множественная линейная регрессия
1. Назовите, в чем состоит спецификация модели множественной регрессии.
2. Сформулируйте требования, предъявляемые к факторам для включения их в модель множественной регрессии.
3. К каким трудностям приводит мультиколлинеарность факторов, включенных в модель, и как они могут быть устранены?
4. Методы устранения мультиколлинеарности факторов.
5. В каких случаях рассчитывается «квази R2»?
6. От чего зависит величина скорректированного индекса множественной корреляции?
7. Как можно проверить наличие гомо- и гетероскедастичности остатков?
Задача 1
По 19 предприятиям оптовой торговли изучается зависимость объема реализации (у) от размера торговой площади (х1) и товарных запасов (х2). Были получены следующие варианты уравнений регрессии:
1) у = 25+15х1 r2 = 0.9
2) y = 42+27 x2 r2 = 0.84
3) y = 30+10x1 + 8x2 r2 = 0.92
(2,5) (4,0)
4)y = 21+ 14x1 + 20x2 + 0.6 x22 R2 = 0.95
(5,0) (12,0) (0,2)
В скобках указаны значения стандартных ошибок для коэффициентов регрессии
Задание
1. Проанализируйте тесноту связи результата с каждым из факторов.
2. Выберите наилучшее уравнение регрессии, обоснуйте принятое решение.
Задача 2
Для изучения рынка жилья в городе по данным о 46 котеджах было построено уравнение множественной регрессии:
y = 21,1-6,2 x1 + 0,95x2 + 3.57 x3 R2 = 0.7
(1,8) (0,54) (0,83)
где
y - цена объекта, тыс. долл.;
x1 - расстояние до центра города, км;
x2 - полезная площадь объекта, кв. м;
x3 число этажей в доме, ед.;
К - коэффициент множественной детерминации.
В скобках указаны значения стандартных ошибок для коэффициентов мно-*ественной регрессии.
1 Проверьте гипотезу о том, что коэффициент регрессии b1 в генеpальной совокупности равен нулю.
2 Проверьте гипотезу о том, что коэффициент регрессии b2 в генеpальной совокупности равен нулю.
3. Проверьте гипотезу о том, что коэффициент регрессии b3 в генеральной совокупности равен нулю.
4. Проверьте гипотезу о том, что коэффициенты регрессии b1, b2 b3 в генеральной совокупности одновременно равны нулю (или что коэффициент детерминации равен нулю).
5. Поясните причины расхождения результатов, полученных в пп. 1, 2 и 3, с результатами, полученными в п. 4.
Задача3
В результате исследования факторов, определяющих экономический рост, по 73 странам получено следующее уравнение регрессии:
G= 1,4-0,52P+ 0,17S+11,16I-0,38D-4,75In, R2 =0,60,
(-5,9) (4,34) (3,91) (-0,79) (-2,7)
где G ~ темпы экономического роста (темпы роста среднедушевого ВВП в % к базисному периоду);
Р - реальный среднедушевой ВВП, %;
S - бюджетный дефицит, % к ВВП;
I - объем инвестиций, % к ВВП;
D - внешний долг, % к ВВП;
Іn - уровень инфляции, %.
В скобках указаны фактические значения t-критерия для коэффициентов множественной регрессии.
Задание
1. Проверьте гипотезу о достоверности полученной модели в целом.
2. До получения результатов этого исследования ваш однокурсник заключил с вами пари, что эмпирические результаты по данной модели докажут наличие обратной связи между темпами экономического роста и объемом внешнего долга страны (% к ВВП). Выиграл ли это пари ваш однокурсник?
Задача 4
По 20 предприятиям легкой промышленности получена следующая информация, характеризующая зависимость объема выпуска продукции у (млн тенге) от количества отработанных за год человеко-часов х1 (тыс. чел.-ч.) и среднегодовой стоимости производственного оборудования х2 (млн тенге.):
| Уравнение регрессии | у = 35+0,06х1 +2,5х2 |
| Множественный коэффициент корреляции | 0,9 |
| Сумма квадратов отклонений расчетных значений результата от фактических |
Задание
1. Определите коэффициент детерминации в этой модели.
2. Составьте таблицу результатов дисперсионного анализа.
3. Проанализируйте полученные результаты регрессионного анализа.
Основная литература: [4, С.90-175], [10], [14]
Дополнительная литература: [20],[22],[23],[25], [32]
Тема № 11 (занятие 14) Анализ временных рядов
1. Перечислите основные элементы временного ряда?
2. Что такое автокорреляция уровней временного ряда и как ее можно оценить количественно
3. Показатели анализа временных рядов.
4. Перечислите методы выравнивания временных рядов.
5. В чем заключается сущность метода сглаживания?
6. В чем сущность метода последовательных разностей?
7. Какова интерпретация параметров уравнения регрессии по первым разностям уровней рядов?
8. Что такое критерий Дарбина – Уотсона?
Задача 1
Администрация банка изучает динамику депозитов физических лиц за ряд лет (млн. долл. в сопоставимых ценах). Исходные данные представлены ниже:
| показатели | годы | сумма | ||||||
| Время, лет | ||||||||
| Депозиты физических лиц, х |
Известно также следующее: ∑ х2 = 511.
Задание
1. Постройте уравнение линейного тренда и дайте интерпретацию его параметров.
2. Определите коэффициент детерминации для линейного тренда.
3. Администрация банка предполагает, что среднегодовой абсолютный прирост депозитов физических лиц составляет не менее 2,5 млн. долл. подтверждается ли предположение результатами, которые вы получили?
Задача 2
Изучается динамика потребления мяса в регионе. Для этого были собраны данные об объемах среднедушевого потребления мяса уt (кг) за 7 месяцев. Предварительная обработка данных путем логарифмирования привела к получению следующих результатов:
| месяц | |||||||
| ln yt | 2,1 | 2,11 | 2,13 | 2,17 | 2,22 | 2,28 | 2,31 |
Задание
1. Постройте уравнение экспоненциального тренда.
2. Дайте интерпретацию его параметров.
Задача 3
Изучается зависимость объема продаж бензина (уt) от динамики потребительских цен (хt). Полученные за последние 6 кварталов данные представлены в таблице:
| показатель | 1кв. | 2кв. | 3кв. | 4кв. | 5кв. | 6кв. |
| Индекс потребительских цен, % к 1 кварталу | ||||||
| Средний за день объем продаж бензина в течение квартала, тыс. л. |
Известно также, что ∑xt = 680, ∑yt = 476, ∑xtyt = 53648, ∑xt2 = 77566.
Задание
1. Постройте модель зависимости объема продаж бензина от индекса потребительских цен с включением фактора времени.
2. Дайте интерпретацию параметров полученной вами модели.
Задача 4
Администрация торговой фирмы интересуется, есть ли взаимосвязь между объемом продаж и удельным весом женин среди работников компании. Для этого были собраны данные за последние девять лет.
| показатель | |||||||||
| Объем продаж, тыс.долл., уt | |||||||||
| Удельный вес женщин среди работников компании, %, хt |
Известны следующие данные; ∑xt = 264, ∑yt = 3788, ∑xtyt = 112001, ∑xt2 = 78388, ∑yt2 = 1604488.
Уравнения трендов для каждого из рядов составили:
а) для ряда хt, хt = 23,5 + 1,17t; б) для рада yt,ŷt = 374.14+3.33t +0.95 t2.
Задание
1. Определите коэффициент корреляции между изучаемыми рядами по их уровням.
2. Определите коэффициент корреляции между изучаемыми рядами по отклонениям от указанных выше линейного и параболического трендов соответственно.
3. Выбрав одну из полученных мер в пп.1 и 2, охарактеризуйте тесноту связи между временными рядами объемов продаж и долей женщин среди работников компании. Обоснуйте ваш выбор.
Задача 5
Годовое потребление товара А и доходы население (тысяч тенге) за 9 лет приведены в таблице
| Показатель | |||||||||
| Потребление | |||||||||
| Доходы |
Задание
1. Определите уравнение регрессии, включив в него фактор времени, если известно, что ∑У = 599, ∑Х = 731, ∑ХУ = 52179, ∑Х2= 64361,
∑У2 = 42367.
2. Интерпретируйте полученные результаты.
Основная литература: [4, С.90-175], [10], [14]
Дополнительная литература: [20],[22],[23],[25]
