С помощью регрессионного анализа строится и проверятся модель связи между одной зависимой (эндогенной) и одной или более независимыми (экзогенными) переменными.
Направление причинной связи между переменными определяется через предварительное обоснование и включается в модель как гипотеза. Регрессионный анализ проверяет статистическую состоятельность модели при данной гипотезе.
Кросс-секционная регрессия проверяет связь между переменными в определенный момент времени. При анализе регрессии во временных рядах данные по каждой из переменных собираются в течение следующих друг за другом периодов времени.
Для статистической проверки взаимосвязи между зависимой и независимой переменными необходимо найти значения параметров. Метод оценки должен быть таким, чтобы это были наилучшие, линейные, несмещенные оценки.
Метод, используемый чаще других для нахождения параметров уравнения регрессии и дающий наилучшие линейные несмещенные оценки – это метод наименьших квадратов.
Для обоснованного приложения МНК к данным и проверки взаимосвязи между переменными данные должны соответствовать допущениям, предполагаемым регрессионной моделью. К ним относятся:
1. случайный член не имеет систематических отклонений в каком – либо направлении;
2. дисперсия случайного члена постоянна для всех наблюдений;
3. случайные члены во всех наблюдениях должны быть независимы друг от друга;
4. случайный член должен быть распределен независимо от объясняющих переменных;
5. случайные члены нормально распределены.
Нарушение условий Гаусса- Маркова может привести к неэффективности оценок коэффициентов регрессии.
Статистическая значимость коэффициентов измеряется степенью вариации вокруг оценочного значения. Для определения степени значимости коэффициентов используются t-критерии. Чтобы их определить, надо знать: выборочное распределение данных коэффициентов; оценки их дисперсий.
Стандартные ошибки коэффициентов – это средние квадратические отклонения.
Тестирование гипотезы, критические значения, уровень значимости, P-значение, доверительные интервалы. Тестирование регрессионного уравнения, обсуждение R2 и t-, F-статистик. Оценки метода максимального правдоподобия.
Основная литература: [4, С.53-114], [11, С.55-94] [10], [14]
Дополнительная литература: [20],[22],[23],[25], [32]
Тема № 8.Парная нелинейная регрессия
Рассмотрим наиболее простые случаи нелинейной регрессии: гиперболу, экспоненту и параболу. При нахождении коэффициентов гиперболы и экспоненты используют прием приведения нелинейной регрессионной зависимости к линейному виду.
Гипербола
При нахождении гиперболы 
вводят новую переменную 
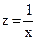, тогда уравнение гиперболы принимает линейный вид 
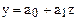. После этого используют формулы (9.3) для нахождений линейной функции, но вместо значений 
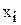используются значения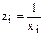 
; 
.
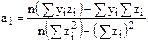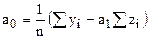При проведении вычислений во вспомогательную таблицу вносятся соответствующие колонки.
Экспонента
Для приведения к линейному виду экспоненты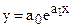 
проведем логарифмирование
;
;
.
Введем переменные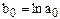 
и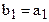 
, тогда 
, откуда следует, что можно применять формулы (9.3), в которых вместо значений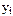 
надо использовать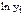 
.
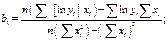
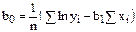При этом мы получим численные значения коэффициентов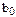 
и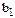 
, от которых надо перейти к 
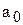и 
, и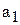спользуемых в модели экспоненты. Исходя из введенных обозначений и определения логарифма, получаем
, 
.
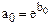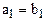Парабола
Длянахождения коэффициентов параболы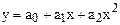 
необходимо решить линейную систему из трех уравнений
Оценка силы нелинейной регрессионной связи
Сила регрессионной связи для гиперболы и параболы определяется непосредственно по формуле (9.2). При вычислении коэффициента детерминации экспоненты все значения параметра Y (исходные, регрессионные, среднее) необходимо заменить на их логарифмы, например, 
– на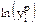 
и т.д.
Основная литература: [4, С.53-114], [11, С.55-94] [10], [14]
Дополнительная литература: [20],[22],[23],[25], [32]
