Задания
Необходимо выполнить разобранные примеры на компьютере.
Пример 1. Предположим, что застройщик оценивает стоимость группы небольших офисных зданий в традиционном деловом районе. Застройщик может использовать корреляционный анализ для установления связи между выбранными переменными.
Переменная Смысл переменной
y Оценочная цена здания под офис, тыс. $;
x1 Общая площадь в квадратных метрах;
x2 Количество офисов;
x3 Количество входов;
x4 Время эксплуатации здания в годах.
В этом примере предполагается, что существует линейная зависимость между каждой независимой переменной (x1, x2, x3 и x4) и зависимой переменной (y), то есть ценой здания под офис в данном районе.
Застройщик наугад выбирает 11 зданий из имеющихся 1500 и получает следующие данные.
| х1 | х2 | х3 | х4 | у |
| 1,5 | ||||
| 1,5 | ||||
"Пол-входа" (1/2) означает вход только для доставки корреспонденции.
Необходимо установить степень тесноты связи между объясняющими переменными и объясняемыми.
Выполнение.
Заполним данными диапазон A1:E12.
1. Для нахождения парной регрессии (например, между площадью и ценой) используем функцию КОРРЕЛ(), указав в окне диалога диапазоны A2:A12 и E2:E12. Полученное значение 0,32 свидетельствует о наличии слабой линейной связи между выбранными переменными.
2. Чтобы найти коэффициенты корреляции между всеми парами переменных воспользуемся средством Корреляция из Анализа данных. В окне диалога необходимо указать входной интервал, наличие меток (подписей к данным) в первой строке, название листа, на котором будут отображены результаты анализа.
Окно диалога «Корреляция».
| х1 | х2 | х3 | х4 | у | |
| х1 | |||||
| х2 | 0,22 | ||||
| х3 | 0,62 | 0,31 | |||
| х4 | 0,22 | -0,05 | -0,05 | ||
| у | 0,32 | 0,88 | 0,51 | -0,45 |
После выполнения анализа из отчета можно увидеть, что в наибольшей степени цена дома определяется количеством офисов в нем (коэффициент корреляции 0,88). Отрицательно на цене сказывается возраст дома, – чем он больше, тем дом дешевле (коэффициент корреляции -0,45). Можно также сделать вывод о существующей линейной зависимости площади дома и количества входов в него – коэффициент корреляции 0,62.
Линейная регрессия.
Регрессионный анализ используется, если две исследуемые переменные не равноправны, то есть изменение одной из переменных служит причиной для изменения другой. Например, рост дохода ведет к увеличению потребления; снижение процентной ставки увеличивает инвестиции; увеличение валютного курса сокращает чистый экспорт. Это - тот случай, когда должно быть оценено уравнение регрессии y=f(x). Уравнение регрессии - это формула статистической связи между переменными. Если эта формула линейна, то речь идет о линейной регрессии. Формула статистической связи двух переменных называется парной регрессией, зависимость от нескольких переменных - множественной регрессией.
Выбор формулы связи переменных называется спецификацией уравнения регрессии; в данном случае выбрана линейная формула. Однако до тех пор, пока не оценены количественные значения параметров, не проверена надежность сделанных оценок, эта формула остается лишь гипотезой. Оценка значений параметром выбранной формулы статистической связи переменных называется параметризацией уравнения регрессии.
Любую прямую можно задать ее наклоном и y-пересечением. Обозначим наклон через a1, а Y-пересечение через a0. Тогда уравнение парной регрессии примет вид y = a1× x + a0
Если известны значения b1 и b0, то можно вычислить любую точку на прямой, подставляя значения y или x в уравнение.
Оценки коэффициентов a в случае парной регрессии рассчитываются по формуле:

 ;
; 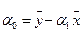
Проверка общего качества уравнения регрессии. Коэффициент детерминации R2
Для анализа общего качества оцененной линейной регрессии используют обычно коэффициент детерминации R2, называемый также квадратом коэффициента множественной корреляции. Для случая парной регрессии это квадрат коэффициента корреляции переменных х и y. Коэффициент детерминации рассчитывается по формуле
 , где еi = yi – a1xi-a0 – разница между теоретическим и реальным значением yi.
, где еi = yi – a1xi-a0 – разница между теоретическим и реальным значением yi.
Он характеризует долю вариации (разброса) зависимой переменной, объясненной с помощью данного уравнения. В качестве меры разброса зависимой переменной обычно используется ее дисперсия, а остаточная вариация может быть измерена как дисперсия отклонений вокруг линии регрессии. Если числитель и знаменатель вычитаемой из единицы дроби разделить на число наблюдений n, то получим, соответственно, выборочные оценки остаточной дисперсии и дисперсии зависимой переменной у. Отношение остаточной и общей дисперсий представляет собой долю необъясненной дисперсии. Если существует статистически значимая линейная связь величин х и у, то коэффициент R2 близок к единице[1].






