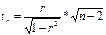Модель именуется адекватной, если прогнозы значений эндогенной переменной согласуются с её наблюденными значениями.
В целом для проверки адекватности модели используются различные тесты, например- Коэффициент детерминации, F-тест, Тест Стьюдента, Ошибка аппроксимации, Тест Дарбина- Уотсона и тест Голфелда-Квандта.
Тест Голфелда-Квандта предназначен для проверки предпосылки теоремы Гаусса-Маркова о гомоскедастичности случайных возмущений в уравнениях наблюдений, т.е. о том, что Var(u1)=Var(u2)=….=Var(un)=σ2
Тест Дарбина- Уотсона. Этот тест предназначен для проверки третьей Cov(ui;uj)=0 при i≠j. Часто истинной причиной неадекватности предпосылки оказывается ошибка в выборе уравнения регрессии в спецификации модели. Данный тест является одним из наиболее важных тестов в эконометрике.
Ошибка аппроксимации. Величина отклонений фактических и расчетных значений результативного признака (y-ˆyx) по каждому признаку представляет собой ошибку аппроксимации (ОА). Чтобы иметь общее суждение о качестве модели из относительных отклонений по каждому наблюдению, находят среднюю ОА как среднюю арифм-кую простую.
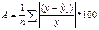 или
или  , где n-число наблюдений
, где n-число наблюдений
F-тест - оценивание качества уравнения регрессии - состоит в проверке гипотезы Н0 о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического Fфакт и критического (табличного) Fтабл значений F-критерия Фишера. Fфакт определяется как
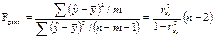
гду n — число единиц совокупности; m - число параметров при переменных х
Fтабл – это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости а. Уровень значимости а - вероятность отвергнуть пра-вильную гипотезу при условии, что она верна. Обычно а принимается равной 0,05 или 0,01.
Если Fтабл<Fфакт, то Н0 - гипотеза о случ-ной природе оцениваемых харак-тик отклоняется и признается их статистическая значимость и надежность. Если Fтабл>Fфакт, то гипотеза Н0 не отклоняется и признается стат-ская незначимость, ненадежность ур-ния регрессии.
Долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака у характеризует коэффициент (индекс) детерминации 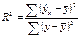
0≤ R2≤1. причем если R2= 1 то переменная полностью объясняется регрессором xt.
Тест Стьюдента. Отношение коэффициента регрессии к его стандартной ошибке дает t-статистику, которая подчиняется статистике Стьюдента при (n-2) степенях свободы. Эта статистика применяется для проверки статистической значимости коэффициента регерссии и для расчета его доверительного интервала.
Фактическое значение t-критерия Стьюдента определяется как