Выражение множественной регрессии в натуральном масштабе будет иметь следующий вид:
у=а+b1x1+b2x2+…+bmxm+ε
bmxm – коэффициенты регрессии. Характеризуют среднее изменение результата с изменением соответствующего фактора на единицу. При неизменном значении других факторов закреплён на их среднем уровне.
ε – остатки.
для того, чтобы найти параметры этого уравнения, мы должны написать систему нормальных уравнений. У нас m+1 неизвестное, значит у нас m+1 уравнение.
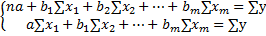
Кроме уравнения в натуральном масштабе во множественной регрессии используется уравнение в стандартизированном масштабе.
ty=β1t1+ β2t2 …βmtm
где tуt1 … tn – стандартизированные переменные, определяющиеся следующим образом:
ty= 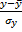 ti=
ti= 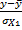
β1 β2… βn – стандартизированные коэффициенты регрессии, которые показывают, на сколько единиц изменится в среднем результат, если соответствующий фактор хiизменится на единицу при неизменном среднем уровне других факторов.
В силу того, что все переменные заданы как центрированные и нормированные, стандартизированные коэффициенты β можно сравнивать между собой.Сравнивая их друг с другом, можно ранжировать факторы по силе их воздействия на результат.
Ф-ла 2
Пусть β1 β2 β5 β4 β3
Коэф-ты в натуральном масштабе регрессии связаны между собой со стандартизированными коэ-ми.
bi=βi 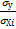
Рассмотренное значение стандартизированных коэф-в регрессии позволяет использовать их при отсеве факторов. Из модели исключаются факторы с наименьшими значениями β. На основе линейного уравнения регрессии в натуральном масштабе могут быть найдены частные уравнения регрессии.
уХ1.Х2Х3…Xm - уравнение зависимости результата от фактора х, при наличии факторов х1 … хm.
ф-ла 3
т.е. это система уравнений, которые связывают результативный признак с соответствующим фактором хiпри закреплении всех прочих факторов на их среднем уровне. При подстановке в это уравнение средних значений соответствующих факторов они примут вид парных линейных регрессий.
В отличие от парной регрессии частные уравнения регрессии характеризуют изолированное влияние на результат соответствующего фактора. Эффект влияния от других факторов обнаруживается (проявляется) в свободном члене А. это позволяет на основе частных уравнений регрессии определять частные коэф-ты эластичности.
Ф-ла 4
Где bi – коэф-т регрессии для фактора хi.
Знаменатель – частное уравнение регрессии. Наряду с частными коэф-ми эластичности рассчитывают средние по совокупности показатели эластичности.
Ф-ла 5
Этот показатель показывает, на скольков среднем изменится результат при изменении фактора на 1%. Средние показатели эластичности можно сравнивать друг с другом и, соответственно, ранжировать их по силе воздействия на результат.
Свойства оценок МНК
Оценки, полученные по МНК, будут обладать свойствами несмещенности, состоятельности и эффективности. Несмещённость оценок означает, что математическое ожидание остатков равно 0. Если это свойство выполняется, то параметры можно сравнивать по разным исследованиям. Оценки считаются эффективными, если они характеризуются наименьшей дисперсией. Степень достоверности доверительных интервалов параметров регрессии обеспечивается, если оценки будут обладать состоятельностью. Состоятельность характеризует увеличение точности с увеличением объёма выборки.
Пример. Имеются данные о сменной добыче угля на одного рабочего (у в тоннах), мощности пласта (х1 в метрах) и уровне механизации работ (х2 в %). Предполагается, что между переменными у, х1, х2 существует корреляционная зависимость. Найдём уравнение регрессии.
| № | Х1 | Х2 | у | Х12 | Х1*Х2 | УХ1 | Х22 | УХ2 | |
| ∑ |
Ф-ла 6
Оно показывает, что при увеличении мощности пласта х1 на 1 метр добыча угля на одного рабочего увеличивается в среднем на 0,854 тонны при неизменном х2. А при увеличении уровня механизации работ х2 (при неизменном х1) на 1%добыча угля у увеличивается в среднем на 0,367 тонны.
Найдем уравнение множественной регрессии в стандартизированном виде.
Ф-ла 7.
Поскольку β1больше β2, то можно сказать, что мощность пласта оказывает бОльшее влияние на добычу угля, чем уровень механизации работ.
Ф-ла 8
Эластичность для первого фактора выше, что говорит о том, что 1ый фактор оказывает бОльшее влияние на результат. Тем самым мы подтвердили выводы.






