Тема 1. Предмет эконометрики
Наука молодая, выделилась как самост. наука в 20г. прошлого века. Эконометрика – измерение в экономике (букв.). Термин был введен в 1926 году норвеж. экономистом Р. Фришем. Представляет собой единство 3х наук – статистика, эк. теория, математика.
Эконометрику определяют как науку о моделировании эк. процессов, позволяющую прогнозировать их развитие, выявлять и измерять определяющие факторы. Наука занимается моделированием эк. явлений (построение матем. моделей). Модель строится для прогнозирования.
Любой процесс построения модели проходит 6 основных этапов:
1. Постановочный. На нём определяются конечные цели моделирования, набор участвующих в модели факторов. Определяется роль факторов.
2. Информационный. Происходит сбор необх. информации, проверка достоверности данных, их сопоставимости. Используются как пространственные, так и временные данные.
3. Спецификация модели. Устанавливаются экзогенные (внешние) и эндогенные (внутренние) переменные. Выявляются связи и соотношения между ними.
4. Идентификация модели – статистический анализ модели, т.е. выявление условий корректного оценивания параметров модели на основе соотношения количественных переменных и связей между ними.
5. Оценка параметров модели.
6. Верификация модели – производится сопоставление реальных и модельных данных, проверка адекватности модели, оценка точности расчётов на основе моделей, получаемых в прогнозах оценок, и производится анализ остатков (случайных величин).
Если модель удовлетворяет всем предъявляемым ей требованиям, то её можно использовать для прогнозирования и для объяснения скрытых механизмов исследуемых процессов. Анализируемые задачи могут относиться к макроуровню (межстрановый), мезоуровню (регионы внутри страны), микроуровню (предприятия, фирмы, семьи).
Показатели вариации
1. СКО σ= 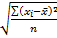 , для несгруппированных данных
, для несгруппированных данных
σ= 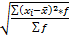 , для сгруппированных данных
, для сгруппированных данных
2. σ2 (дисперсия) – средний квадрат отклонения значения признака от средней величины
σ2=  , для несгруппированных данных
, для несгруппированных данных
σ2= 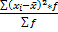 , для сгруппированных данных
, для сгруппированных данных
σ2= 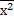 –
–  2, где
2, где 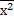 =
=  , и
, и  2=
2= 
3. V (коэффициент вариации) - наиб. часто применяемый на практике– процентное отношение среднего квадратического отклонения к средней арифметической величине признака

По величине V судят об однородности совокупности. Чем >V тем < однородная совокупность, тем < типична средняя для данной совокупности.
Совокупность считается однородной, если V не превышает 30%. Средняя степень однородности 30-60%.
4.  Моментный коэффициент асимметрии:
Моментный коэффициент асимметрии: 
Если As<0, асимметрия – левосторонняя. Если As>0, асимметрия – правосторонняя. Если  , асимметрия – незначительная. Если
, асимметрия – незначительная. Если  , асимметрия – значительная. Для нормального распределения А=0.
, асимметрия – значительная. Для нормального распределения А=0.
Excel: Данные – анализ данных – описательная статистика.
Показатели динамики
Для характеристики развития явления во времени применяются следующие показатели:
1. Абсолютный прирост. Базисный  где yt уровень дин ряда в момент времени. Цепной
где yt уровень дин ряда в момент времени. Цепной 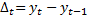 .
.
Абсолютный прирост показывает, на сколько единиц уровень одного периода больше или меньше уровня другого периода.
2. Коэф-т роста. Базисный -  . Цепной -
. Цепной -  .
.
Коэффициент роста характеризует интенсивность изменения уровней ряда.
3. Темп роста – то же, что и коэффициент роста, только выражен в %, а не в разах.
Базисный -  . Цепной -
. Цепной -  .
.
4. Коэффициент прироста характеризуют абсолютный прирост в относительных величинах. Базисный -  ,
,  . Цепной -
. Цепной -  ,
, 
5. Темп прирост а – то же, что и коэффициент прироста, только выражен в %.
Базисный –  ,
,  . Цепной -
. Цепной -  ,
,  .
.
6. Абсолютное значение 1% прироста. Базисный - 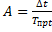 ,
,  . Цепной -
. Цепной -  ,
, 
Понятие о корреляционной связи
При взаимосвязи признаков одни рассматриваются как факторы, влияющие на изменения других признаков – факторные признаки (х). Признаки, изменяющиеся под действием факторных признаков, называются результативными (у).
Пример. Если изучается зависимость спроса на товары, то спрос – результативный, предложение товара – факторный признак.
Статистическая связь проявляется в массовых явлениях, при которых значению факторного признака соответствует множество значений результативного признака. При этом признаки могут быть, как количественными, так и качественными.
Корреляционная связь – статистическая связь, при которой изменение значения факторного признака вызывает различные изменения средних значений результативного признака. Корреляционная связь изучается только по количественным признакам. Слово «корреляция» означает соответствие.
Если рассматривается связь средней величины результативного признака с одним фактором, корреляция называется парнойу=f(x). Если факторов несколько, корреляция – множественнаяy=f(x1, x2…xn).
По характеру изменения фактора и результата парной корреляции различают нелинейную и линейную зависимость. Линейная зависимость бывает прямой и обратной.
Прямая связь график 1.
Пример. Чем больше стаж работы, тем выше производительность труда. Чем выше производительность, тем меньше себестоимость.
При исследовании корреляционной связи рассматривают следующие вопросы:
1. Выявление наличия связи;
2. Количественная оценка тесноты связи с помощью специальныхкоэф-в;
3. Построение математической модели связи, в которой среднее значение результативного признака рассматривается как функция одного или нескольких факторов (занимается регрессионный анализ).
Парная корреляция
Парная корреляция позволяет оценить тесноту связи. Для выявления корреляционной связи можно построить поле корреляции.
Поле корреляции – поле точек, координаты которых (х,у) определяются значениями факторного и результативного признаков. Расположение точек на поле корреляции позволяет судить о наличии связи и о её характере (линейная, нелинейная). Рисунок 1.
По полю корреляции мы выдвигаем только гипотезу. Глядя на одно и то же поле, мы можем судить как о линейной, так и о нелинейной связи.
Пример. Изучается зависимость оценки (у), полученной на экзамене 8 студентами от суммы баллов (х), набранных ими в течение семестра.
| № студента | Оценка на экзамене (у) | Сумма баллов (х) | xi-xср | Yi-yср | (xi-xcp)2 | (yi-ycp)2 | (xi-xcp)*(yi-ycp) | y^ | yi-y^ | (yi-y^)2 |
| -23 | -1,75 | 40,25 | 2,172 | 0,172 | ||||||
| -17 | -0,75 | 12,75 | 2,586 | 0,414 | ||||||
| -1 | -0,75 | 0,75 | 3,69 | 0,69 | ||||||
| -2 | 0,25 | 3,621 | 0,349 | |||||||
| 0,25 | 4,104 | 0,104 | ||||||||
| 0,25 | 4,38 | 0,38 | ||||||||
| 1,25 | 4,725 | 0,275 | ||||||||
| 1,25 | 4,794 | 0,206 | ||||||||

| 7,5 | 2,62 |
у
х
Для измерения тесноты корреляционной связи используют парныйлиненыйкоэф-т корреляции.
 =
=  . Коэф-т парной корреляции измеряется от -1 до 1. Чем ближе к 1 по модулю, тем теснее связь. Симметричная мера связи.
. Коэф-т парной корреляции измеряется от -1 до 1. Чем ближе к 1 по модулю, тем теснее связь. Симметричная мера связи.
Квадрат r – коэф-т детерминации, более предпочтителен, т.к. может быть использован для измерения и нелинейных связей.
Если значения отклонения от среднего значения совпадают, то коэф-т больше (связь прямая). В противном случае – связь обратная.
Если rxy=0, то связь отсутствует. Чем ближе значение к 1, тем связь теснее. Если =1, то связь функциональная. Чем он ближе к 0, тем связь слабее.
Коэф-т корреляции – симметричная функция, т.е.rxy=ryx.
ryx<0,3 – слабая связь;
0,3<rxy<0,7 заметная связь;
rxy>0,7 – тесная связь;
rxy>0,9 – очень тесная связь.
Посчитаем коэф-т парной линейной корреляции для примера. Для этогопосчитаем следующие показатели.
 =
=  =648/8=81
=648/8=81
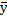 =
=  =30/8=3,75
=30/8=3,75
σ= 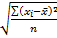 =
=  =12,99
=12,99
σ=  =
=  =0,97
=0,97
rxy= 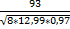 =0,92
=0,92
rxy2-коэф-т детерминации. Показывает долю вариации результативного признака под действием факторного признака. 0<rxy2<1. Чем ближе значение к 1, тем больше вариация результативного признака обусловлена вариацией факторного признака. Чем ближе к 0, тем меньше. Коэф-т вариации может выражаться в %.
rxy2=0,85 или 85%. Значит сумма накопленных за семестр баллов объясняет 85% различий в оценках, полученных на экзамене. 15% зависит от других факторов.
Если связь установлена, целесообразно перейти к 3му этапу – построению матем. функций.
Парная линейная регрессия
Уравнение, описывающее корреляционную связь между зависимой переменной у и одной независимой переменной х, называется парной регрессией. При выборе типа функции руководствуются характером расположения точек на поле корреляции, а также содержанием изучаемой связи, которая обеспечивает наилучшую аппроксимацию поля корреляции.
Когда влияние изменения фактора на результат постоянно, то обычно используют линейную функцию. В других случаях – используют нелинейную функцию.
у=а+bx
у-среднее значение результативного признака при определённом значении факторного признака х; а – свободный член уравнения регрессии, не имеющий экономической интерпретации (лишь математическую); b – коэф-т регрессии, показывает среднее изменение результата при изменении фактора на 1 единицу. Коэф-т детерминации показывает…
Построение регрессионной модели включает следующие основные этапы:
1. Определение цели исследования;
2. Оценка однородности исходных данных;
3. Выбор формы связи между результатом и признаком;
4. Определение параметров модели (a&b);
5. Оценка тесноты связи;
6. Определение показателей эластичности;
7. Проверка качества построенной модели.
Вначале оценим однородность исходных данных. Для этого рассчитаем коэф-т вариации. 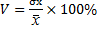 =12,99/81*100%=16,0%
=12,99/81*100%=16,0%
Построим уравнение регрессии. Найдём параметры а и b парной линейной регрессии. Для этого используем метод наименьших квадратов (НМК). Исходным условием для нмк является то, что нужно подобрать такую прямую у=а+bx, которая отражает минимальную сумму квадратов отклонений фактических значений результативной переменной от её теоретических значений, получаемых на основе уравнения регрессии.  àmin
àmin
уi- фактические значения результативного признака y^i – теоретические значения.
f(a,b)=∑(yi-(a+bx))2àmax
Чтобы найти минимум функции, надо вычислить частные производные по каждому из параметров и приравнять их к 0.

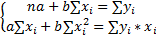
Получаем систему нормальных уравнений.
у=а+bх
b=  = rxy*
= rxy* 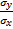
a= 
Вернёмся к нашему примеру.
b=(0,92*0,97)/12,99=0,069
а=3,75-0,069*81=-1,83
запишем теоретическое уравнение:
у^=-1,83+0,069х.
Коэф-т корреляции и параметр b должны быть одного знака, т.к. они показывают направление связи.
Коэф-т регрессии b показывает, что с ростом накопленных за семестр баллов на одну единицу оценка за экзамен увеличивается на 0,069 от своего среднего значения.
Направление связи между результатом и фактором определяется знаком коэф-та регрессии. В отличие от коэф-та корреляции коэф-т регрессии b является асимметрической хар-кой связи, т.к. показывает зависимость изменения у от х.
Коэффициент эластичности
Для оценки влияния фактора на результативный признак вычисляют коэф-т эластичности. Средний коэф-т эластичности для парной линейной регрессии будет рассчитываться по формуле 
Единицы измерения этого коэф-та - % (но умножать на 100 не нужно).
Он показывает,на сколько % в среднем изменяется результативный признак от своего среднего значения при изменении среднего факторного признака на 1%.
 0,069*(81/3,75)=14,9%
0,069*(81/3,75)=14,9%
Значит, что при увеличении накопленных за семестр баллов на 1% от своего среднего значения оценка за экзамен увеличивается на 14,9%.
Проверка качества построенной модели.
Для оценки качества построенной модели, рассчитаем теоретические значения экзаменационной оценки для каждого студента. Подставляем в y^=-1,83+0,069*58=2,172






