Различают 2 класса нелинейных регрессий:
1. Регрессии нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам.
к ним относятся:
парабола у=a+bx+cx2
y=a+b/x – равносторонняя гипербола
у=b*lnx – полулогарифмическая функция
у=axb – степенная
у=abx-показательная
у=еа+bx - экспоненциальная
2. Регрессии, нелинейные по оцениваемым параметрам
Регрессии, нелинейные по включенным переменным приводятся к линейному виду простой заменой переменных, а дальнейшая оценка параметров производится методом НМК.
у=a+bx+cx2
Z=x2
y=a+bx+cz
И неизвестные параметры мы находим методом НМК.
y=a+b/x
z=1/x
y=a+bz
b= 
a= 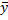 -b
-b 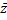
| у | Х | Z | Z |
| 0,5 | ln2 | ||
| 0,25 | ln4 |
Мы работаем с z, чтобы найти параметры а и b.
Нелинейные модели 2го класса, в свою очередь, делятся на 2 типа:
1. Нелинейные модели внутренне-линейные (приводятся к линейному виду с помощью соответствующих преобразований, например, логарифмированием). Сюда относятся показательная, степенная, экспоненциальная, логистическая у=а/(1+becx), обратная у= 1/(а+bх)
2. Нелинейные модели внутренне нелинейные (не приводятся к линейному виду).
y=а+bxc
Среди всех нелинейных функция наиболее часто используется степенная функция, которая приводится к линейному виду логарифмированием у=a*xb
log y = log a*xb
log y = lna+lnxb
log y = ln a +b ln x
log y = Y, ln a = A, ln x = X
Y=A+bX.
| х | у | Х | Y |
| ln 1 | ln 3 | ||
| ln 2 | ln 4 |
Далее делается операция, обратная логарифмированию – потенцирование:
ln y = A+bln x
ln y = G
y=eG
i.e. y=eA+blnx
y=eA+ebln x
y=eA+xb
В нелинейных функциях такую интерпретацию имеет параметр b.
Параметр b в степенной функции является коэф-м эластичности, который показывает, на сколько % в среднем изменится результат при изменении фактора на 1% от его среднего значения.
Коэф-т эластичности для нелинейных функций: Э=f’(x)* 
Эср = f’(xcp)* 
Таблица расчета средних коэф-в эластичности для наиболее используемых уравнений регрессий:
| Вид функции у | f’(x) | Эср |
| y=a+bx | b | b* 
|
| у=a+bx+cx2 | b+2cx | 
|
| у=а+b/x | -b/x2 | - 
|
| y=a*xb | ab*x-1 | |
| y=a+bln x | b/x | b/(a+bln x cp) |
| y=1/(a+bx) | -b/(a+bx)2 | -bx/(a+bxcp) |
a+bxcp - среднее значение у. Эластичность получается сразу в %.
Бывают случаи, когда для рассматриваемых признаков бессмысленно изменение в %. В этих случаях коэф-т эластичности не рассчитывают.
Для уравнений нелинейной регрессии определяют показатель тесноты связи. В это случае он называется индексом корреляции.
ρxy= 
σ2y(общая) = 
 =
= 
Квадрат индекса корреляции носит название индекса детерминации и характеризует долю дисперсии результативного признака у, объясняемую регрессией в общей дисперсии результативного признака.
ρxy2=1-(σ2ост/σ2ост)=σ2факторная/σ2у
σ2факт= 
Индекс детерминации можно сравнивать с коэф-м парной линейной детерминации для обоснования возможностей применения линейной функции. Чем больше кривизна линии регрессии, тем меньше величина парного линейного коэф-та детерминации по сравнению с индексом детерминации.
Индекс детерминации используется для проверки существенности в целом уравнения регрессии по F-критерию Фишера.
Fф=(ρxy2/(1-ρxy2))*(n-m-1)/m
n-m-1 = k1
m=k2
m- число параметров при х
Сравниваем с табличным значением, если оно больше фактического, то уравнение считается статистически значимым. Fтабл = (α, k1, k2)
О качестве нелинейного уравнения можно судить также, используя ошибку аппроксимации, которая вычисляется аналогично линейной функции.
Пример.
Поэтому отбор факторов обычно осуществляется в 2 стадии:
1. Подбираются факторы, исходя из сущности проблемы;
2. На основе матрицы показателей корреляции определяют факторы для параметров регрессии. Корреляция между объясняющими переменными позволяет исключить из модели дублирующие факторы.
Считается, что 2 переменные явно коллинеарны (находятся между собой в линейной зависимости), если парныйкоэф-т корреляции между ними больше 0,7. rXiXj>0,7.
Если факторы явно коллинеарны, то один из них дублирует другого, а значит, один из них надо исключить из модели. Предпочтение при этом отдаётся не фактору, тесно связанному с результатом, а фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами.
Пример. Пусть матрица коэф-в парной корреляции оказалась следующей:
| У | Х1 | Х2 | Х3 | |
| У | ||||
| Х1 | 0,8 | |||
| Х2 | 0,7 | 0,6 | ||
| Х3 | 0,8 | 0,5 | 0,2 |
y=f(х1, х2, х3).
Оставляем тот фактор, который менее тесно связан с результатом – х2. Убираем х1.
(Excel- анализ данных – корреляция – матрица корреляции).
При наличии мультиколлинеарности факторов, т.е. когда более, чем 2 фактора, связаны между собой линейной связью, имеет место совокупное воздействие факторов друг на друга. Наличие мультиколлинеарности означает, что некоторые факторы будут всегда действовать в унисон, в результате вариация исходных данных не будет являться независимой, а следовательно, нельзя будет оценить воздействие каждого фактора в отдельности. Наличие мультиколлинеарности приводит к следующим последствиям:
1. Затрудняется интерпретация параметров множественной регрессии, они теряют экономический смысл;
2. Оценки параметров ненадёжны, обнаруживаются большие стандартные ошибки, что делает модель непригодной для анализа и прогнозирования.
Для оценки мультиколлинеарности факторов используют определитель матрицы парных коэф-в корреляции между факторами. Если бы факторы не коррелировали между собой, то матрица парных коэф-в была бы единичной, т.к. все диагональные коэф-ты были бы равны 0.
Пусть нам дано уравнение регрессии следующего вида:
y=a+b1x1+b2x2+b3x3
1-матрица
∆r= 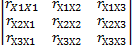 =
=  =1
=1
Если наоборот – между факторами существует полная линейная зависимость, то и все коэф-ты корреляции будут равны единице, т.е. (матрица 2)
∆r=  =0
=0
и её определитель будет равен 0. Следовательно, чем ближе к 0 определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадёжнее результаты множественной регрессии (мультиколлинеарность – это плохо =)).
Чем ближе к 1 – тем меньше мультиколлинеарность факторов.
Существует ряд подходов преодоления сильной межфакторной корреляции. Самый простой путь – убрать из модели один или несколько факторов. 2ой подход связан с преобразованием факторов, при котором уменьшается корреляция между ними.Существует много способов отбора факторов в модель. Наибольшее применение получили следующие:
1. Метод исключения – рассматривается полный набор факторов, а потом отсеиваются факторы из полного набора.
2. Метод включения – дополнительное введение факторов.
3. Шаговый регрессионный анализ –исключение ранее введённого фактора.
При отборе факторов рекомендуется пользоваться следующим правилом: число включаемых факторов в 6-7 раз должно быть меньше объёма совокупности, по которой строится регрессия. Если это соотношение нарушается, то число степеней свободы остаточной дисперсии очень мало. Это приводит к тому, что уравнение регрессии оказывается статистически незначимым, т.е. F-критерий меньше табличного значения.




