Середнє арифметичне значення вибірки (просто середнє) 
– середня величина, що згладжує індивідуальні відмінності та визначає найбільш характерні ознаки
,
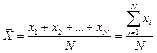де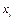 
– значенняваріанти; N – кількість варіант у вибірці. Якщо ж у досліджуваній сукупності окремі варіанти повторюються, то розраховується зважене середнє
.
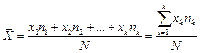Середнє арифметичне має наступні властивості:
▲ збільшується (зменшується) на яку-небудь величину, якщо у досліджуваній вибірці кожну варіанту збільшити (зменшити) на ту ж величину;
▲ збільшується (зменшується) у k разів, якщо кожну варіанту збільшити (зменшити) у k разів;
▲ сума усіх позитивних і негативних варіант від середньої арифметичної дорівнює нулю, тобто сума відхилень значень, що спостережуються, від середньої арифметичної дорівнює нулю;
▲ сума квадратів відхилень варіант від середньої арифметичної – найменша величина у порівнянні з сумою квадратів відхилень варіант тієї ж сукупності від будь-якої величини, відмінної від середньої арифметичної.
Для повної характеристики вибірки поряд з середньою арифметичною вводять показник варіабельності ознаки, який називають дисперсією. Це абсолютна міра нестабільності, розмірність якої відповідає розмірності ознаки, що вивчається, у другому ступені
.
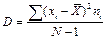Середньоквадратичне відхилення (стандартне відхилення) характеризує варіювання ознаки довкола середньої арифметичної, має ту ж розмірність, що й ознака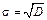 
. Якщо розмірність ознак різна, то визначають їхні коефіцієнти варіації, які характеризують відносну міру нестабільності
.
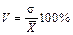У спортивній практиці прийнятні наступні значення варіацій:
● V = 0-10 % – невелика;
● V = 11-20 % – середня;
● V > 20 % – велика.
Для значного числа випадкових величин, що зустрічаються у практиці, можна чекати розподілу їхніх значень згідно із законом нормального розподілу, який носить ім’я Гауса-Лапласа. Функція щільності нормального розподілу значень має вигляд, який приведено на рис. 2.2.
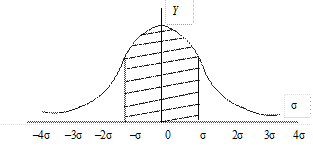
Рис. 2.2. Крива нормального розподілу значень випадкової величини
Якщо перенести начало координат у центр розподілу, то криву можна розглядати як лінію розподілу випадкових похибок, де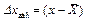 
. При цьому дійсне значення наближається до середнього арифметичного, з чого витікає низка властивостей:
▲ позитивні і негативні випадкові помилки рівно можливі, про що свідчить симетрична крива;
▲ середнє арифметичне із алгебраїчної суми значень випадкових помилок при необмеженому зростанні спостережень прагне до нуля, про що також свідчить симетрична крива;
▲ малі за абсолютною величиною випадкові помилки зустрічаються при спостереженнях частіше, ніж великі, про що свідчить кілообразна крива;
▲ вірогідність того, що випадкові похибки не вийдуть за межі «плюс-мінус» складає 0.682 (~68 %). Це означає попадання у заштриховану площу приблизно у два рази більше, ніж у не заштриховану, тобто в цьому випадку вірогідність появи малих похибок більша, а великих менша.
Асиметрія або коефіцієнт асиметрії є мірою несиметричного розподілу. Якщо коефіцієнт асиметрії значно відрізняється від нуля, розподіл асиметричний, про що свідчить відношення
.
Ексцес або коефіцієнт ексцесу вимірює гостроту піку розподілу за формулою
.
Асиметрію та ексцес використовують для перевірки нормальності розподілу. Якщо коефіцієнт асиметрії та ексцес дорівнюють нулю, то має місце нормальний розподіл змінної. Розподіл із гострішою вершиною, ніж нормальний, має позитивний ексцес, а із більш закругленою – негативний. При зростанні об’єму вибірки збільшується точність оцінок.
Для характеристики правильності оцінки служить показник, який носить назву помилка репрезентативності, величина якої зменшується при збільшенні обсягу вибірки
.
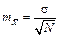Для вибірок малого об’єму (N < 30) використовується формула
.
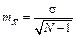Математичне очікування випадкової величини є таким її значенням, довкола якого групуються результати окремих спостережень і яке для дискретних величин обусловлюють сумою добутків усіх можливих варіант ряду на вірогідність (частість)
.
Медіана 
Ме – це варіанта, що знаходиться у середині варіаційного ряду і розбиває відповідну вибірку на дві рівні частини. Одна половина спостережень лежить нижче за медіану, інша – вище. Наприклад, у гімнастиці п’ять експертів поставили наступні оцінки у балах: 9; 9.1; 9.2; 9.3; 9.4. Значення медіани дорівнює 9.2 бали (Ме = 9.2). Якщо число спостережень непарне (n = 2 m + 1), то медіана оцінюється як х (m); med = х (m), а якщо парне (n = 2 m), то як med = 0.5(х (m) + х (m + 1)). Медіана має важливу властивість, яка заключається у тому, що сума абсолютних відстаней між точками вибірки та медіаною мінімальна.
Квантіль – це число, яке відповідне перцентілям (відсоткам), нижче за яке знаходиться такий же об’єм вибірки. Наприклад, квантіль дорівнює 0.75, тобто значення варіанти таке, нижче за яке знаходяться 75 % значень інших варіант.
Квартілі (від слова «кварта» – чверть) – нижня та верхня чверті, які мають відповідні значення розподілів 25 % і 75 %. Отже, нижня квартіль, медіана і верхня квартіль ділять вибірку на чотири рівні частини. Це означає, що 25 % спостережень лежить між мінімальним значенням і нижньою квартілью, 25% – між нижньою квартілью і медіаною, 25% – між медіаною і верхньою квартілью, а 25% – між верхньою квартілью і максимальним значенням вибірки. Квартільний розмах – інтервал, що містить медіану, у який потрапл яє 50 %спостережен ь.
Мода Мо – варіанта у ряді розподілів, яка найчастіше зустрічається, інакше кажучи найбільш модна. Якщо розподіл має декілька мод (декілька піків), то його називають мультімодальным. Мультімодальність при суддівських оцінках у спорті говорить про те, що існує декілька певних різних думок експертів. При необмеженому обсязі вибірки мода й медіана сходяться до середнього значення генеральної сукупності.
