При проведенні повторних спостережень (вимірів) однієї й тієї ж величини в однакових умовах можна отримати результати, які збігаються або відрізняються один від одного. Це говорить про наявність у спостереженнях випадкових помилок (похибок), що проявляються без явного закономірного зв’язку із попередніми спостереженнями.
Властивості випадкових подій у великих сукупностях вивчає теорія вірогідності. Випадковою подією називають таке явище, яке при здійсненні певного комплексу умов може статися або не статися. Випадкові помилки (відхилення) бувають будь-якими за величиною чи за знаком.
Вірогідність події – це кількісна оцінка об’єктивної можливості її появи. Вірогідність достовірної події дорівнює одиниці, а неможливої – нулю. Обидві ці події невипадкові. Якщо зіштовхнути який-небудь об’єкт з горизонтальної опори, то він полетить униз і це буде достовірною подією, а не вгору, що вважатиметься неможливою подією. Події вірогідності появи, яких більше нуля і менше одиниці, випадкові.
У результаті спостережень явищ масового характеру було встановлено, що певна подія зберігає стійку частоту появи по відношенню до спільного числа усіх подій даного типу. Відношення частоти до числа дослідів називають частістю. При повторних спостереженнях схожих явищ така подія з’являється з тією ж частотою. Тому частість появи подій при необмеженому збільшенні числа однорідних незалежних дослідів мало відрізнятиметься від їх вірогідності. Результати явищ масового характеру більш-менш відрізняються один від одного, тобто значення яких-небудь параметрів завжди зазнають випадкове розсіювання. Але масові вимірювання однорідних об’єктів, що володіють якісною спільністю, виявляють певні закономірності. Дослідженнями і створенням методів виявлення цих закономірностей займається математична статистика.
Математична статистика – наука, яка вивчає результати масових вимірів, що повторюються [2, 4].
Основні положення статистичних досліджень у спорті
У спортивній практиці використовують такі основні етапи статистичних досліджень [3, 8]:
■ спостереження, які являють собою планомірний, науково-обгрунтований збір даних, що характеризує об’єкти, які підлягають вивченню, і задовольняє наступним вимогам. Об’єкти спостереження (у нашому випадку спортсмени і фізкультурники, яких будуть випробувати) мають бути однаковими (однорідними) з точки зору їх властивостей: кваліфікації, спеціалізації, віку, спортивного стажу й тому подібного. Число цих об’єктів повинно бути таким, щоб була можливість виявити закономірності та узагальнити їхні властивості;
■ відомості, які включають систематизацію даних та угрупування і оформлення певних статистичних таблиць;
■ аналіз статистичного матеріалу за допомогою математично-статистичного методу.
У процесі спостереження або вимірювання якого-небудь показника для випробовуваних спортсменів одержують ряд чисел. Чисельні результати підрозділяють на дискретні (від англійського слова «diskrete», що означає переривчастий) і безперервні. До дискретних відносять, наприклад, число підтягувань чи спроб, тобто результати, виражені цілим числом. Як безперервні результати можна розглядати час проходження дистанції, час реакції, швидкість руху й таке інше. Їх можна виражати дробовим числом, зокрема безконечним дробом.
Підготовка результатів статистичних спостережень
Досліджень
Після певних спостережень фіксують чисельні результати яких-небудь показників групи спортсменів. Якщо 
– результат виміру показника, що вивчається, у 1-го спортсмена, 
– у 2-го й т.д., а всього спортсменів N, то такий результат, представлений випадковими числами, називають вибірковою сукупністю або вибіркою. Сукупність усіх значень, які можна було б отримати для вибірки, що вивчається, називають генеральною сукупністю. Наприклад, числові значення довжини тіл студентів конкретної групи – це вибірка, а числові значення довжини тіл студентів усього університету – генеральна сукупність. Так, якщо розглядати цей параметр для всіх вузів, наприклад, Харкова по відношенню до НТУ «ХПІ», то це буде генеральна сукупність, а саме для університету – вибірка.
Кожне числове значення з вибірки називають варіантою. Кількість варіант характеризує об’єм вибірки, позначений через N. Генеральну сукупність можна представити загальною сукупністю об’єктів спостереження спортсменів, які володіють тими ж властивостями, що й об’єкти вибірки. Задача математичної статистики при побудові модельних характеристик спортсменів, при встановленні різних видів норм, з урахуванням точності вимірів, які створюють, – це оцінка генеральної сукупності на основі вивчення вибірки обмеженого об’єму. Для цього необхідно, щоб вибірка, яка досліджується, була типовою та добре репрезентувала структуру генеральної сукупності. Об’єм вибірки має бути таким, щоб закономірності загальної властивості були характерними для генеральної сукупності.
Після того, як сформована сукупність, тобто отримана низка випадкових чисел, проводять її первинну обробку, яка включає угрупування результатів спостережень. Початковий масив значень вибірки перетворюють у низку, де варіанти розташовані у зростаючому або убиваючому порядку. Таку операцію називають ранжируванням. Потім варіанти розміщують у вигляді подвійного ряду або стовпця з урахуванням їхньої повторюваності. Таким чином впорядкований числовий ряд, в якому вказана повторюваність варіантів, називають варіаційним рядом. Числа, що показують кількість повторень варіанти 
, – це частоти або ваги.
Вибірки великого об’єму розбивають на інтервали. Число інтервалів k, що рекомендується для вибірок різного об’єму, наведено у табл. 2.1.
Таблиця 2.1
| Об’єм вибірки N |  10-20
| 30-50 | 60-90 | 100-120 | 300-400 |
| Число інтервалів k | 5-6 |
Якщо необхідно відібрати гірших і кращих спортсменів, то величину або крок інтервалу визначають за формулою
,
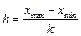де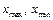 
– максимальний і мінімальний результати у вибірці. Далі для наглядності малюють гістограму розподілу значень – столбчатий графік. Термін «гістограма» у 1985 році запропонував К. Пірсон. Гістограми дозволяють визначати у різних інтервалах частоту значень змінних. Вони зручні для використанні при великому числі спостережень, бо показують, які саме значення змінної, що досліджується, або їхні діапазони найбільш часто зустрічаються, як вони розрізняються між собою, яка концентрація спостережень навколо середнього арифметичного має місце, яка симетричність розподілу та кількість мод (стовпців) розподілу й так далі. За формою розподілу значень, наприклад, за наявністю двох високих стовпців (двох мод), можна зробити висновок про те, що вибірка неоднорідна та складається з варіант, які належать двом різним генеральним сукупностям. Вигляд гістограми визначає, який закон розподілу вона має, та на основі цього вибирають відповідні статистичні критерії.
На рис. 2.1 варіаційний ряд представлений у вигляді ступінчастої кривої. На осі абсцис відкладені відрізки, що відображують інтервал, а на осі ординат – відрізки, що відповідають частотам або частостям окремих варіант. На цій основі збудовані прямокутники з висотами, відповідними частотам або частостям інтервалів. При малих інтервалах ступінчаста крива переходить у плавну криву.
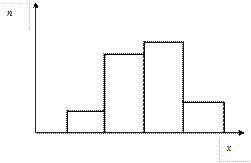
Рис. 2.1. Гістограма розподілу значень випадкової величини
