У української мові складні речення одержують із двох інших за допомогою союзів і, а, якщо... то, або, або, тоді й тільки тоді, коли й ін. Назвемо такі й аналогічні їм союзи логічними зв'язуваннями. Нові речення з'являються також із уживанням частинки не або слів невірно, що….. Ці слова також будемо називати логічними зв'язуваннями.
Тоді стверджувальні речення, (не утримуючі \ утримуючі) логічні зв'язування, називають (елементарними \ складовими) висловленнями. Наприклад, пропозиція «Всі програмісти мають вищу або середню фахову освіту» складається із двох елементарних пропозицій: «Всі програмісти мають вищу фахову освіту» і «Всі програмісти мають середню фахову освіту». З'єднано речення зв'язуванням або.
Пропозиція «Якщо програміст не має фахової освіти, то він не буде конкурентоспроможний на ринку праці» складається із простих пропозицій, з'єднаних зв'язуваннями якщо... то й заперечень не. Однак не завжди граматична форма пропозицій, у яких виражене судження, збігається з його логічною формою. Так, складне судження може бути представлено простою пропозицією. Наприклад: «Дискретна математика включає розділи: «Елементи теорії множин», «Елементи теорії графів», «Елементи класичної й математичної логіки», «Елементи теорії автоматів». Це складне судження хоча й представлено простою пропозицією, але містить п'ять простих суджень.
Оскільки мовою алгебри логіки служать буліви функції, то природно значеннєвим зв'язуванням поставити у відповідність операції над булівими змінними.
Якщо просте висловлення є істинним, то йому відповідає значення логічної змінної 1. Якщо просте висловлення є помилковим, то йому відповідає значення логічної змінної 0. Якщо виконується все (складене) висловлення, то воно називається істинним і йому відповідає 1, якщо не виконується, то висловлення вважається помилковим і йому відповідає 0. Складене висловлення можна розглядати як буліву функцію, де аргументами є семантичні характеристики простих висловлень, що входять у складне, а значенням буде семантична характеристика всього висловлення. Залишається тільки встановити відповідність між синтактическими зв'язуваннями російської мови й булівими операціями.
Для того щоб визначити, істинно або хибне деяке складне висловлення, використовують таблиці істинності, у яких латинськими буквами позначаються самі висловлення, а цифрами 1 і 0 їхня семантична характеристика — відповідно «істина» або «неправда». Наприклад, висловлення «Місто X розташоване на березі Дніпра» (А)може бути істинним (при Х = Канів А = 1) або помилковим (при Х= Харків А = 0).
Основними операціями є: заперечення (не), диз'юнкція (строга) (або) і нестрога (або)), кон’юнкція (і), імплікація (якщо... то), еквіваленція (тоді й тільки тоді). Природно, вони визначаються на основі уведених раніше відповідних булівих функцій з обліком чисто логічної специфіки.
Уведемо визначення логічних операцій.
Запереченням, або інверсією, висловлення А називається висловлення 
яке істинно, коли висловлення А хибне, і хибне, коли А істинне.
Диз'юнкцією (нестрогої або сполучної) висловлень А і В називається висловлення 
яке істинно тоді й тільки тоді, коли істинно хоча б одне із цих висловлень.
Кон’юнкцією висловлень А і В називається висловлення 
, що істинно тоді й тільки тоді, коли істинні обоє висловлення.
Строгою диз'юнкцією висловлень А і В називається висловлення 
яке істинно тоді й тільки тоді, коли істинно тільки одне із цих висловлень.
Імплікацією висловлень А і В називається висловлення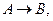 
яке хибне тоді й тільки тоді, коли з істини випливає хибність.
Еквіваленцієй висловлень А і В називається висловлення 
яке істинно тоді й тільки тоді, коли або істинні, або помилкові одночасно обоє висловлення.
Наприклад, для простих висловлень «Максимов — гарний програміст» (А)і «Він перемагає на олімпіадах» (В)можна скласти складні висловлення.
Кон’юнкція : «Максимов — гарний програміст, і він перемагає на олімпіадах» або «Максимов — гарний програміст, він перемагає на олімпіадах».
Нестрога диз'юнкція 
«Або Максимов гарний програміст, або перемагає на олімпіадах».
Строга диз'юнкція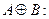 
«Або Максимов гарний програміст, або перемагає на олімпіадах».
Імплікація 
«Якщо Максимов гарний програміст, то він перемагає на олімпіадах»; «Для того щоб Максимов перемагав на олімпіадах, досить,щоб він був гарним програмістом».
Еквіваленція 
«Максимов гарний програміст тоді й тільки тоді, коли він перемагає на олімпіадах». «Максимов гарний програміст тільки коли він перемагає на олімпіадах».
Помітимо, що операція заперечення не завжди виражена в явному виді за допомогою слова невірно або частки не перед дієсловом. Наприклад, для висловлення 
(А) заперечення може бути представлено варіантами: «невірно, що , «X не більше 5» або 
а також 
або 
Для висловлення «Пряма а, що лежить на площині, не перетинає окружність» (А)запереченням служать висловлення: «Невірно, що пряма а, що лежить на площині, не перетинає окружність», «Пряма а, що лежить на площині, перетинає окружність», «Пряма а, що лежить на площині, має з окружністю загальні точки»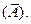 
Однак додавання частки не й слова невірно може не перетворити висловлення А в негативне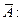 
«Максимов — гарний програміст» і «Невірно, що Максимов — гарний програміст», тому що мова може йти про різних Максимових. Тому для одержання висловлень, протилежних даним, необхідно враховувати загальні правила побудови суперечливих суджень А і 
Якщо висловлення має вигляд елементарного речення без квантора спільності, то не перед дієсловом дійсно замінить висловлення А на його заперечення
Складемо словник перекладу з української мови на мову алгебри логіки й включимо в нього таблиці істинності логічних операцій (табл. 4.5).
З порівняння визначень логічних операцій, операцій над множинами й відповідними колами Ейлера можна укласти, що диз'юнкції (логічній сумі) відповідає об'єднання множин, кон’юнкції (логічному добутку) — перетинання (добуток) множин, строгої диз'юнкції (сумі по модулю 2) — пряма сума, запереченню — різниця, імплікації — підмножина. Оборотний увага, що фактично у визначенні множин були використані логічні зв'язування й, або, не й ін. У такому випадку виникають проблеми з визначеннями, адже виходить замкнуте коло. Саме тому ми вважаємо за необхідне введення логічних операцій тільки через відповідні буліви функції, значення яких уводяться постулативне.
Визначення логічних операцій цілком базуються на відповідних булівих функціях і теорії множин. Всі вони, крім імплікації, є зрозумілими й безперечними. Що стосується імплікації, то на перший погляд не очевидно, чому свідомо помилкове висловлення (наприклад, «2,53 є натуральним числом») може приводити до будь-якого твердження (наприклад, «Перший політ людини в космос був в 1961 р.»). Також бентежить, що щиро імплікацію двох не зв'язаних логічно між собою щирих висловлень, наприклад «17 - просте число» і «XXI в. почався з 2001 р.». Тому саме ця логічна операція буде розглянута докладно в наступному підрозділі.
Таблиця 4.5
Словник перекладу на мову алгебри логіки
