Тому що відношення на М задаються підмножинами,  (або
(або 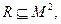 якщо
якщо  для них визначні ті ж операції, що й над множинами:
для них визначні ті ж операції, що й над множинами:
1. Об'єднання 
 або
або 
2. Перетинання 
 і
і 
3. Різниця 
 і
і 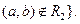
4. Доповнення R:
 де
де 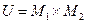 (або
(або 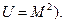
Крім того, визначають інші операції над відношеннями, у тому числі:
5. Зворотне відношення  існує тоді й тільки тоді, коли існує bRа:
існує тоді й тільки тоді, коли існує bRа:

Наприклад, якщо R - "бути молодше", то  - "бути старше", якщо R - "бути сином", то
- "бути старше", якщо R - "бути сином", то  - "бути батьком (або матір'ю)".
- "бути батьком (або матір'ю)".
6. Складене відношення (композиція) 
Нехай задані множини  й відношення
й відношення  й
й  Складене відношення діє з
Складене відношення діє з 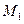 у
у 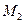 за допомогою
за допомогою 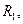 а потім з
а потім з 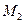 у
у  за допомогою
за допомогою  тобто
тобто  якщо існує таке
якщо існує таке  що
що  й
й  На рис.1.8 показані множини
На рис.1.8 показані множини  , у них - області визначень
, у них - області визначень 
 і області значень
і області значень  і
і  заштриховані
заштриховані

Рис.1.8
у різних напрямках для  й
й  Сегменти з подвійним штрихуванням на
Сегменти з подвійним штрихуванням на  являють собою
являють собою  й
й  відповідно.
відповідно.
Зокрема, якщо відношення R визначене на множині 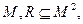 то складене відношення
то складене відношення 
Наприклад, якщо R - "бути сином", те  - "бути онуком".
- "бути онуком".
Позначимо  Використовуючи це позначення, можна визначити
Використовуючи це позначення, можна визначити  для будь-якого
для будь-якого  в такий спосіб:
в такий спосіб:
 і
і 
7. Транзитивне замикання 
Транзитивне замикання  складається з таких і тільки таких пар елементів а,b з М, тобто
складається з таких і тільки таких пар елементів а,b з М, тобто  для яких у М існує ланцюжок з (k+2)елементів
для яких у М існує ланцюжок з (k+2)елементів  між сусідніми елементами якої виконується R:
між сусідніми елементами якої виконується R:  тобто:
тобто:
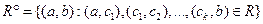 (визначення I).
(визначення I).
Унарна операція транзитивного замикання  може бути також визначена як нескінченне об'єднання:
може бути також визначена як нескінченне об'єднання:
 (визначення II).
(визначення II).
Наприклад, для відношення R - "бути сином" складене відношення (композиція)  - "бути онуком",
- "бути онуком",  - "бути правнуком" і т.д. Тоді об'єднання всіх цих відношень є транзитивне замикання
- "бути правнуком" і т.д. Тоді об'єднання всіх цих відношень є транзитивне замикання  - "бути прямим нащадком".
- "бути прямим нащадком".
Якщо відношення R транзитивно, то  Наприклад, транзитивне замикання відношення R - "бути більше" збігається із цим відношенням, тобто
Наприклад, транзитивне замикання відношення R - "бути більше" збігається із цим відношенням, тобто 
8. Рефлексивне замикання 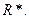
Нехай тотожне відношення  Тоді
Тоді

Якщо R транзитивно й рефлексивно, то 
Процедура обчислення транзитивного замикання  для відношення
для відношення 
1) привласнити 
2) обчислити  привласнити
привласнити 
3) зрівняти:  Якщо
Якщо  то привласнити
то привласнити  й перейти до кроку 2. У противному випадку - до кроку 4;
й перейти до кроку 2. У противному випадку - до кроку 4;
4) кінець: 
Функція як бінарне відношення. Часткові і повні функції. Відображення. Класифікація функцій. Зворотна функція. Композиція функцій
Якщо відомо, що А і В — упорядковані множини з відношеннями порядку, аналогічними « » і «
» і « », і
», і 
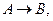 то можна дати визначення для монотонних функцій: функція
то можна дати визначення для монотонних функцій: функція  називається монотонної \ строго монотонної, якщо із
називається монотонної \ строго монотонної, якщо із  випливає, що
випливає, що 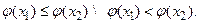
На множині пар дійсних чисел (множина точок площини) частковий порядок можна задати за допомогою покоординатного попередування, а повний - якщо поставити порядок однієї з координат як пріоритетний.
Функціональні відношення. Функціональними відношеннями,або функцією,називається бінарне відношення для якого кожному елементу х з області визначення ставиться у відповідність єдиний елемент у з області значень. Якщо відношення і йому зворотне є функціональними, то функція визначає взаємо-однозначнувідповідність, або бієкцію.
a) Відношення  називається функціональним, якщо для кожного
називається функціональним, якщо для кожного  перетин R по х містить не більше одного елемента).
перетин R по х містить не більше одного елемента).
Приклад. Задамо таблицею на рис. 10.3 деяке відношення  яке повністю задовольняє умові функціональності, оскільки на кожній вертикалі перебуває жирна точка, і притім єдина. Побудуємо стрілочне подання цього відношення (рис. 10.3): як видно з рисунка, з кожної точки виходить стрілка, і притім тільки одна (включаючи цикли).
яке повністю задовольняє умові функціональності, оскільки на кожній вертикалі перебуває жирна точка, і притім єдина. Побудуємо стрілочне подання цього відношення (рис. 10.3): як видно з рисунка, з кожної точки виходить стрілка, і притім тільки одна (включаючи цикли).
Якщо перетин R по будь-якому елементі з А містить один (і тільки один) елемент, то функціональне відношення називається всюди певним.
Приклад. Відношення, представлене на рис. 10.3.
Якщо відношення 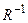 ,симетричне до функціонального відношення
,симетричне до функціонального відношення  теж функціонально, то відношення R називається взаємно однозначним.
теж функціонально, то відношення R називається взаємно однозначним.

Рис. 10.3.
Приклад. Зображена нижче таблиця, у якої в кожному рядку й у кожному стовпці рівно одна жирна точка, представляє взаємно однозначне відношення. Подання цього відношення за допомогою перетинів має вигляд:
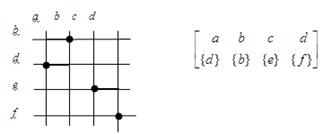
d) Для всякого функціонального відношення, взаємно однозначного чи ні, визначимо функцію, пов'язану із цим відношенням, як функцію, перетин якої по кожному  або порожньо, або є той елемент множини В, що є елементом R(x).
або порожньо, або є той елемент множини В, що є елементом R(x).
Перетин R(x) множини R по  називають образом аргументу х для функції
називають образом аргументу х для функції  й позначають
й позначають 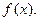 Аргумент також називають змінною, а
Аргумент також називають змінною, а  — значенням функції. Перетин
— значенням функції. Перетин  множини R по
множини R по  називають прообразом у для функції
називають прообразом у для функції 
Множина  , таких, що існує
, таких, що існує  є область визначення.
є область визначення.
Якщо образ всієї множини А дорівнює В, інакше кажучи, якщо кожен елемент із В є образ принаймні одного елемента з А, то говорять, що має місце відображення А на В; говорять також, що  є сюр¢єктівне відображення функції, пов'язаної з R. Якщо
є сюр¢єктівне відображення функції, пов'язаної з R. Якщо  всюди визначена, тобто якщо область визначення збігається з А, то говорять, що
всюди визначена, тобто якщо область визначення збігається з А, то говорять, що  є відображення множини А в В і пишуть
є відображення множини А в В і пишуть 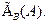 Якщо А і В збігаються, тобто
Якщо А і В збігаються, тобто  відображення множини А в А, елемент х, що задовольняє відношенню
відображення множини А в А, елемент х, що задовольняє відношенню 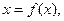 називається нерухомою точкою відображення
називається нерухомою точкою відображення 
Якщо  -функція, пов'язана з R, то, коли R — взаємно днозначне відношення, функція, пов'язана з
-функція, пов'язана з R, то, коли R — взаємно днозначне відношення, функція, пов'язана з  позначається
позначається  В цьому випадку
В цьому випадку  називається ін¢єктивної (говорять також однозначної) функцією, а
називається ін¢єктивної (говорять також однозначної) функцією, а  — оберненною функцією.
— оберненною функцією.
Якщо, крім того, R усюди визначено, тобто  ін¢єктивне відображення, або ін'єкція. Тоді
ін¢єктивне відображення, або ін'єкція. Тоді 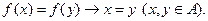
Бієктивними відображеннями, або бієкціями, називаються відображення одночасно сюр¢єктивні й ін¢єктивні.
Приклади. а) (Відображення множини А на множину В.)Нехай  — множина дійсних чисел. Функція
— множина дійсних чисел. Функція 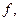 яка визначена формулою
яка визначена формулою  —2 (читається: х переходить в y = 3 х — 2), задає відображення множини А на множину В.
—2 (читається: х переходить в y = 3 х — 2), задає відображення множини А на множину В.
b) (Відображення множини А в множину В.) Нехай знову  . Функція
. Функція  така, що
така, що  є відображення множини А в В. Тут знову
є відображення множини А в В. Тут знову  -множина дійсних чисел. Це відображення не сюр¢єктивне, тому що негативні числа із множини В не є образами елементів з А при відображенні f.
-множина дійсних чисел. Це відображення не сюр¢єктивне, тому що негативні числа із множини В не є образами елементів з А при відображенні f.
c) Нехай А — множина R дійсних чисел, і В - множина  позитивних дійсних чисел, відображення
позитивних дійсних чисел, відображення  яке ставить у відповідність кожному елементу з А деякий елемент із В, взаємно однозначно; дійсно кожному у відповідає
яке ставить у відповідність кожному елементу з А деякий елемент із В, взаємно однозначно; дійсно кожному у відповідає 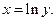
Отже маємо ін¢єктивне відображення.
Оберненне відображення до відображення  буде відображення
буде відображення 
d) Нехай функція  визначена на множині А, і функція
визначена на множині А, і функція  визначена на множині
визначена на множині  якщо для кожного
якщо для кожного  то
то  називається обмеженням функції
називається обмеженням функції 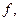 а
а  — продовженням функції
— продовженням функції  Якщо дані множини А,
Якщо дані множини А,  і
і  задані на
задані на  , то
, то  повністю визначено. Зворотне невірно: так, симетрію щодо точки М у площини Р можна розглядати як обмеження різних перетворень простору в себе, наприклад симетрії простору щодо крапки М або симетрії відносно прямій, ортогональної до Р у точки М.
повністю визначено. Зворотне невірно: так, симетрію щодо точки М у площини Р можна розглядати як обмеження різних перетворень простору в себе, наприклад симетрії простору щодо крапки М або симетрії відносно прямій, ортогональної до Р у точки М.
Таблиця 1.6.
Властивості бінарних відношень
| Множина | Відношення | Рефлек- тивність | Симет- ричність | Асиметрич- ність | Антисиме-тричність | Транзити- вність | Антитран- зитивність |
| Будь-які | 
| + | - | - | + | + | - |
| Будь-які не порожні | 
| + | + | - | - | - | - |
| Будь-які | 
| - | + | - | - | - | - |
| Будь-які | 
| + | + | - | - | + | - |
| Будь-які | 
| - | + | - | - | - | + |
| N | 
| + | - | - | + | + | - |
| R | 
| - | - | + | - | + | + |
| R | 
| + | - | - | + | + | + |
| R | 
| - | - | + | - | + | + |
| R | 
| + | - | - | + | + | + |
| Прямі площини | 
| + | + | - | - | + | - |
| Прямі площини | 
| - | + | - | - | - | - |
Вектори 
| Колінеар-ність

| + | + | - | - | + | - |
| окружність | дотик | + | + | - | - | - | - |
| окружність | концент-ричність | + | + | - | - | + | - |
| N | Взаємна простота | - | + | - | - | - | - |
| N | 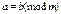 (порівняня за модулем m) (порівняня за модулем m)
| + | + | - | - | + | - |






