Розглянемо буліви функції, представлені у вигляді суперпозиції елементарних функцій «І», «АБО», «НЕ». Використовуючи закони алгебри логіки, можна замінити громіздкі буліви функції їм рівносильними, але більше простими. Такий процес називається мінімізацією булівих функцій. Його проводять для спрощення складних логічних виражень у програмах, а також для того, щоб побудовані на їхній основі функціональні схеми не містили зайвих елементів.
Мінімізувати буліви функції треба, приводячи їх до так званої нормальної форми.
Існують два різновиди нормальних форм - диз'юнктивні (ДНФ) і кон’юнктивні (КНФ). Уведемо визначення.
Елементарною (кон’юнкцією \ диз'юнкцією)називається вираження, що складається з кінцевого числа змінних і їхніх заперечень, узятих у цьому вираженні не більше одного разу й розділених операціями (кон’юнкції \ диз'юнкції):
де 
або 
наприклад 
— елементарна кон’юнкція;
де або наприклад 
— елементарна диз'юнкція.
(Диз'юнктивної \ кон’юнктивної) нормальною формою називається (диз'юнкція \ кон’юнкція) кінцевого числа елементарних (кон’юнкцій \ диз'юнкцій). Скорочено вони позначаються ДНФ і КНФ відповідно.
Нормальна форма називається досконалою, якщо в кожній її елементарній диз'юнкції (кон’юнкції) представлені всі змінні, вхідні в дану функцію (або самі, або із запереченням).
Будь-яка буліва функція й будь-яка формула алгебри логіки можуть бути представлені множиною різних диз'юнктивних форм, рівносильних між собою. Наприклад: 
і т.д.
Із всіх різних ДНФ функції 
особливо виділяється останнє логічне вираження, що є досконалою ДНФ, скорочено ДДНФ. На ДДНФ накладаються наступні вимоги:
Ø формула не є тотожно-хибною;
Ø формула наведена до одного з видів ДНФ;
Ø з формули вилучені елементарні кон’юнкції, що включають одночасно змінну і її заперечення, відповідно до закону протиріччя;
Ø з формули вилучені однакові елементарні кон’юнкції, крім однієї, відповідно до правила ідемпотентності;
Ø кожна елементарна кон’юнкція в ДНФ включає всі логічні змінні (або їхні інверсії), що входять у цю формулу.
Якщо в логічній функції не виконується остання вимога, то в неповну елементарну кон’юнкцію необхідно ввести додатковий множник, що включає диз'юнкцію відсутньої змінної і її заперечення. Це завжди можна зробити, тому що відповідно до закону виключення третього 
а також 
Так, у розглянутому прикладі 
є ДНФ. Для того щоб привести її до ДДНФ, необхідно в першої елементарної кон’юнкції мати змінні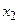 
й 
або їхнього заперечення. Для цього двічі помножимо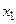 
на 1, для того щоб потім ці одиниці замінити диз'юнкціям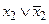и 
й 
відповідно:
Отримана ДНФ є досконалою, тому що відповідає всім перерахованим вимогам.
Аналогічно будь-яку формулу, що має вид КНФ, можна привести до досконалої кон’юнктивної нормальної форми (ДКНФ), для якої виконуються вимоги:
• формула не є тотожно-хибною;
• формула наведена до одному з видів КНФ;
• з формули вилучені однакові елементарні диз'юнкції, крім однієї;
• кожна елементарна диз'юнкція в КНФ включає всі логічні змінні, вхідні в цю формулу.
Якщо логічна функція має вигляд КНФ, то привести її до виду досконалою КНФ (скорочено ДКНФ) можна, доповнивши кожну елементарну диз'юнкцію логічним нулем, що у наступному кроці заміняється на кон’юнкцію відсутньої змінної і її заперечення, тобто відповідно до закону протиріччя: 
а також 
.
Для приклада розглянемо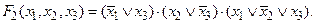 
Вона має вигляд КНФ, але в першій дужці немає змінної 
а в другий — 
Скориставшись наведеним правилом, приведемо її до виду ДКНФ. Тоді маємо:
= 
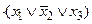Отримана кон’юнктивна нормальна форма є досконалою.
Для порівняння приведемо приклади нормальних форм (табл. 4.19).
Для того щоб привести буліву функцію до досконалої нормальної форми, треба виконати операції в наступному порядку.
Таблиця 4.19
Приклади нормальних форм
Ø Використовуючи рівносильності алгебри логіки, замінити всі наявні операції на кон’юнкцію, диз'юнкцію й заперечення.
Ø Застосовуючи закони Де Моргана, зняти заперечення з логічних операцій кон’юнкції й диз'юнкції.
Ø Використовуючи розподільний і інші закони, привести функції до нормальної форми.
Ø Використовуючи закони ідемпотентності, склеювання й ін., мінімізувати отримані буліви вираження.
Ø Застосовуючи правила операцій з константами, привести мінімізовані нормальні форми до досконалого виду.
Розглянемо приклад. Привести буліву функцію 
до досконалої нормальної форми.
Спочатку приведемо функцію до виду ДКНФ. Маємо:
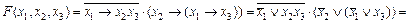
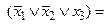
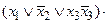
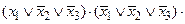
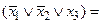
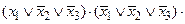
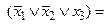
Приведемо спрощену функцію до виду ДДНФ:
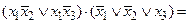
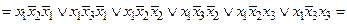
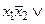
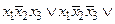
Отримане булево вираження дійсно має вигляд ДДНФ, тому що кожна елементарна кон’юнкція містить всі змінні цієї булівої функції, які зустрілися по одному разу. Знаючи ДДНФ, можна скласти таблицю істинності відповідної функції.
Нехай 
Для одержання таблиці істинності підставимо у функцію значення логічних змінних у кожному рядку й, виконавши дії з логічними константами, знайдемо значення функції. Це набагато простіше, ніж розписувати кожний стовпець у вихідній функції (табл. 4.20).
Досконалі нормальні форми потрібні, наприклад, у тих змістовних задачах, де необхідно розглянути всі можливі варіанти інформації про кожну зі змінних, вхідних у дану буліву функцію.
