Універсальною називають множину U, щоскладається із всіх можливих елементів, які володіють даною ознакою. Наприклад, множина планет Сонячної системи U = {Земля, Марс, Венера, Юпітер, Сатурн, Уран, Плутон, Меркурій, Нептун}. Помітимо, що поняття універсальної множини чітко не визначено, тобто некоректно, U можна включити в іншу множину W, і вона теж буде універсальної. Наприклад, довго вважалося, що множина дійсних чисел 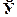 універсальна (тобто описує всю математику), поки не відкрили поле комплексних чисел
універсальна (тобто описує всю математику), поки не відкрили поле комплексних чисел 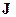 й не зрозуміли, що не існує універсальної числової множини. Проте там, де область об'єктів не виходить за рамки якоїсь множини, іноді буває зручно оперувати із цим терміном.
й не зрозуміли, що не існує універсальної числової множини. Проте там, де область об'єктів не виходить за рамки якоїсь множини, іноді буває зручно оперувати із цим терміном.
Рівними називають дві множини А і В, щоскладаються з однакових елементів: 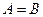 . Наприклад, рівні множини рішень рівнянь
. Наприклад, рівні множини рішень рівнянь 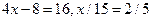 і
і 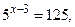 тому що їхнім рішенням є те саме число 6. Рівні множини букв, з яких складені слова «навіс» і «вісна». Рівними множинами є: корені рівняння
тому що їхнім рішенням є те саме число 6. Рівні множини букв, з яких складені слова «навіс» і «вісна». Рівними множинами є: корені рівняння 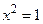 й множина
й множина 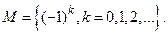 Тому задача «вирішити рівняння» - у реальності означає «вирішити рівняння в якійсь множині». Так, рівняння
Тому задача «вирішити рівняння» - у реальності означає «вирішити рівняння в якійсь множині». Так, рівняння 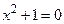 не має дійсних коренів:
не має дійсних коренів: 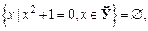 але має два комплексних корені
але має два комплексних корені 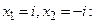
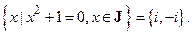 Рівність двох множин А і В означає також, що одночасно
Рівність двох множин А і В означає також, що одночасно  й
й 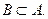 Інавпаки, виконання властивостей
Інавпаки, виконання властивостей 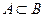 і
і 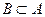 означає виконання рівності А = В. Ці твердження рівносильні. Число елементів множини А називається потужністю множини й позначається
означає виконання рівності А = В. Ці твердження рівносильні. Число елементів множини А називається потужністю множини й позначається 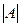 або
або 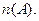 Так, потужність порожньої множини дорівнює 0:
Так, потужність порожньої множини дорівнює 0: 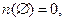 а потужність множини планет Сонячної системи
а потужність множини планет Сонячної системи 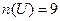 або
або 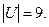
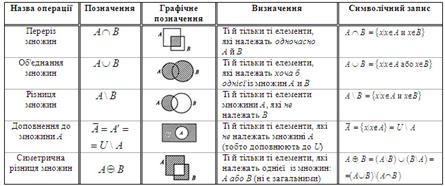
Введення операцій над множинами. З даних множин А і В можна побудувати нові множини за допомогою операцій об'єднання, перетинання, віднімання й ін. (табл. 1.1).
Таблиця 1.1
Основні операції над множинами
Приклад перший. Окружність — множина точок площини, рівновіддалених від даної (наприклад, точки 0), називаної центром. Математично для її знаходження треба задати рівняння рівновіддаленості 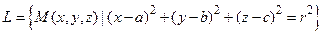 (а це рівняння кола) і рівняння площини, що проходить через центр 0 зкоординатами
(а це рівняння кола) і рівняння площини, що проходить через центр 0 зкоординатами 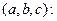
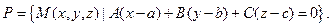 Окружністю (Е) буде множина точок, що належать колу (L),і площини (Р),тобто їхнє перетинання:
Окружністю (Е) буде множина точок, що належать колу (L),і площини (Р),тобто їхнє перетинання: 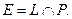 Тому для знаходження цих точок треба вирішити систему двох рівнянь.
Тому для знаходження цих точок треба вирішити систему двох рівнянь.  Отже, окружність
Отже, окружність
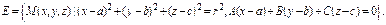
Приклад другій. Нехай 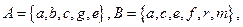 тоді
тоді 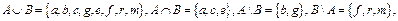
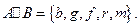
Зверніть увагу, що для різниці двох множин не виконується комутативний закон: 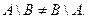 Це стає очевидним, якщо одна множина порожня (наприклад, А),а інша — непуста.
Це стає очевидним, якщо одна множина порожня (наприклад, А),а інша — непуста.
Властивості операцій над множинами. Операції над множинами володіють рядом властивостей, схожих на властивості операцій додавання й множення чисел. Розглянемо закони, справедливі для будь-яких множин А, В, С.
1. 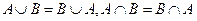 — комутативний закон для операцій об'єднання й перетинання. Оскільки (а це неважко довести) цю властивість справедливо для будь-якого кінцевого числа множин, то зручно використовувати знаки
— комутативний закон для операцій об'єднання й перетинання. Оскільки (а це неважко довести) цю властивість справедливо для будь-якого кінцевого числа множин, то зручно використовувати знаки  й
й 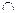 для позначення об'єднання й перетинання багатьох множин. Наприклад,
для позначення об'єднання й перетинання багатьох множин. Наприклад, 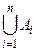 означає об'єднання п множин поза залежністю від того, яке з них уважати першим, другим і т.д.
означає об'єднання п множин поза залежністю від того, яке з них уважати першим, другим і т.д.
2. 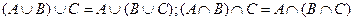 — сполучний закон (асоціативність) для операцій об'єднання й перетинання.
— сполучний закон (асоціативність) для операцій об'єднання й перетинання.
3. 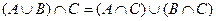 — розподільний закон (дистрибутивність) перетинання щодо об'єднання множин.
— розподільний закон (дистрибутивність) перетинання щодо об'єднання множин.
4. 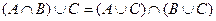 — розподільний закон об'єднання щодо перетинання множин.
— розподільний закон об'єднання щодо перетинання множин.
5. 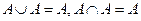 — закони ідемпотентності.
— закони ідемпотентності.
6. 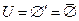 і
і 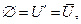 тобто універсальна й порожня множини є доповненнями одна другої.
тобто універсальна й порожня множини є доповненнями одна другої.
7. Якщо позначити через 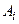 всі підмножини
всі підмножини 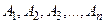 множини А,то будуть справедливі рівності:
множини А,то будуть справедливі рівності: 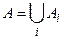 і
і 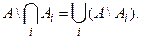
Операція доповнення володіє рядом характерних властивостей.
8. Для будь-якої множини  справедливо (інволюція)
справедливо (інволюція) 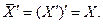
9. Для будь-яких двох множин X і Y справедливо (закон де Моргана): якщо 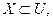
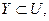 те
те 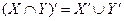 або
або 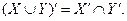
Доведемо останню властивість.
Нехай 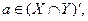 що рівносильно
що рівносильно 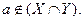 Це значить, що
Це значить, що 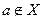 або
або 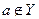 , тобто
, тобто 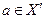 або
або 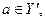 тому
тому 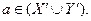
10. Множину А можна розбити на класи непересічних підмножин 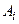 , якщо:
, якщо:
• об'єднання всіх підмножин збігається із множиною А: 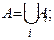
• перетинання будь-яких двох різних підмножин порожньо, тобто для будь-яких 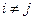 виконується
виконується 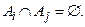
Упорядковані елементи. Відношення на множинах (двомісні і багатомісні). Декартовий добуток. Область визначення й область значень двомісного відношення. Зворотне відношення. Композиція відношень
Двомісним, або бінарним, відношенням R називається підмножина пар 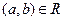 прямого добутку
прямого добутку 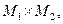 тобто
тобто 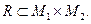 При цьому множину
При цьому множину 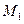 називають областю визначення відношення R, амножину
називають областю визначення відношення R, амножину 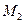 - областю значень. Часто розглядають відношення R між парами елементів тої самої множини М,тоді
- областю значень. Часто розглядають відношення R між парами елементів тої самої множини М,тоді 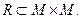 Якщо а, b перебувають у відношенні R,це часто записується як аRb.
Якщо а, b перебувають у відношенні R,це часто записується як аRb.
Нехай 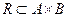 визначено відповідно до зображення на рис.1.1. Область визначення
визначено відповідно до зображення на рис.1.1. Область визначення 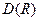 й область значень
й область значень 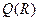 визначаються відповідно:
визначаються відповідно:
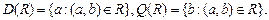
Рис. 1.2
Основні поняття. Відповідність між рівними множинами А = В називається відношенням на даній множині (А). Відношення в деяких числових множинах можуть виражатися термінами: «бути рівним», «бути більше», «бути не менше», «бути дільником» і т.д.
Відношення в множині ліній на площині можуть виражатися термінами: «бути паралельними», «перетинатися», «стосуватися» і т.д.
Назвемо n- місцевим відношенням R на непустій множині М підмножину 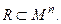 При п = 2 відношення R називається бінарним. Тобто бінарним відношенням між елементами множин А і В називають будь-яка підмножину R множини
При п = 2 відношення R називається бінарним. Тобто бінарним відношенням між елементами множин А і В називають будь-яка підмножину R множини 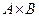 й записують
й записують 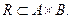 Для відношення R зворотним є відношення
Для відношення R зворотним є відношення 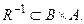 Бінарні відношення прийнято записувати у вигляді
Бінарні відношення прийнято записувати у вигляді 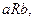 де
де 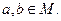 Запис читається як «
Запис читається як «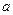 і
і 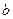 перебувають у відношенні
перебувають у відношенні 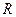 ».
».
Наприклад, 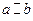 (паралельні прямі),
(паралельні прямі), 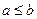 (дійсні числа),
(дійсні числа), 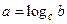 і т.д.
і т.д.
Розглянемо приклади бінарних відношень.
У школі докладно вивчають відношення 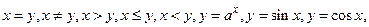
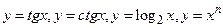 й ін.
й ін.
Графіки прямих і зворотних бінарних відношень, певних на множині дійсних чисел, симетричні щодо бісектриси I і III квадрантів. Це властивість зворотних бінарних відношень використовують при побудові графіків зворотних функцій 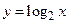 і
і  й
й 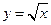 де
де  (рис. 3.2, а);
(рис. 3.2, а); 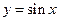 і
і 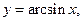 де
де 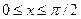 (рис. 3.2, б).
(рис. 3.2, б).
Побудова однозначної зворотної функції можливо лише для монотонних функцій, тому при побудові графіків функцій, зворотних квадратичної і тригонометричної, були уведені обмеження. Для функції 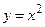 зворотну будували не для всієї області визначення, а лише для ненегативних значень х, тобто на інтервалі, де функція зростає.
зворотну будували не для всієї області визначення, а лише для ненегативних значень х, тобто на інтервалі, де функція зростає.
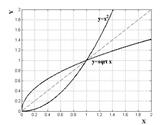
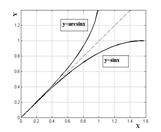
а) б)
Рис. 3.2. Графіки прямих і зворотних бінарних відношень:
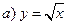 і
і 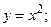

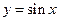 й
й 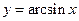
Декартів добуток. Нехай задані множини 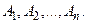 Декартівим (прямим) добутком цих множин називається множина, яка складається із всіх кортежів
Декартівим (прямим) добутком цих множин називається множина, яка складається із всіх кортежів 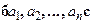 довжини
довжини 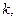 в якій
в якій 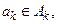 де
де  Оскільки для завдання кортежу важливий порядок, то порядок множників важливий і в декартівому добутку.
Оскільки для завдання кортежу важливий порядок, то порядок множників важливий і в декартівому добутку.
Наприклад, декартівим добутком множин 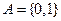 і
і 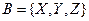 буде множина пар
буде множина пар 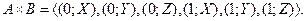
Дужки для вказівки пар опускають там, де це не може привести до затруднень: 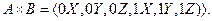
Якщо множини 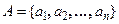 й
й 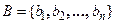 кінцеві, то їх декартів добуток може бути представлений в загальному виді таблицею зі
кінцеві, то їх декартів добуток може бути представлений в загальному виді таблицею зі 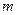 стовпців і
стовпців і 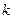 рядків.
рядків.
Таблиця 1.5

| 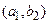
| … | 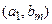
|
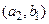
| 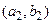
| … | 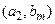
|
| … | … | … | … |
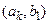
| 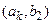
| … | 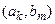
|
Табличне завдання декартіва добутку 
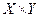
| 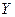
| |||
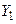
| 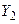
| 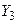
| ||
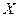
| 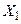
| 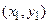
| 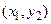
| 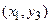
|
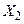
| 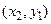
| 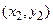
| 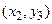
| |
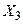
| 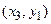
| 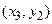
| 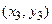
| |
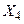
| 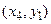
| 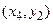
| 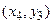
|
Наприклад, декартів добуток 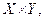 де
де 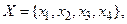 а
а 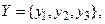 можна представити у вигляді табл. 1.5.
можна представити у вигляді табл. 1.5.
Число елементів у декартівому добутку кінцевих множин А і В дорівнює добутку числа елементів множини А на число елементів множини В. Варіанти запису: 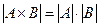 або
або 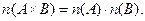
Якщо 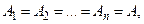 то пишуть
то пишуть 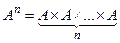 і називають n- й декартівим ступенем множини А.
і називають n- й декартівим ступенем множини А.
Наприклад, площина є декартівим квадратом двох прямих і позначається відповідно 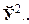 У фізики просторово-часовий континуум є декартів добуток
У фізики просторово-часовий континуум є декартів добуток 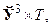 де
де 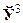 — тривимірний простір, а
— тривимірний простір, а 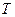 — числова вісь часу.
— числова вісь часу.
Декартів добуток не володіє комутативним законом, тобто, загалом кажучи, пари (а, b)і (b, а)різні: 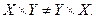 Так, різні точки площини з координатами (5; 3) і (3; 5). Але для довільної й порожньої множин справедливо
Так, різні точки площини з координатами (5; 3) і (3; 5). Але для довільної й порожньої множин справедливо 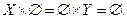
Прикладами декартівих добутків є таблиці додавання й множення, всі можливі набори пар координат на площині, трійок координат деякої точки в просторі. Залізничний квиток теж є кортежем, а сукупність всіх квитків - декартівим добутком множин паспортів, посадкових станцій, станцій прибуття, часу й інших множин.
Якщо число елементів множини X позначити 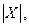 то справедливо співвідношення
то справедливо співвідношення 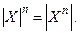
Властивості бінарних відношень. Приведемо характерні властивості бінарних відношень, причому помітимо, що кожне конкретне відношення може володіти або не володіти деякими із зазначених властивостей.
1. Рефлективність: 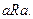 Наприклад, «бути не більше» на
Наприклад, «бути не більше» на 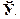
2. Антирефлективність. Має місце, коли відношення не має властивість 1 для будь-яких а, наприклад «бути більше», «бути молодше» і ін.
3. Симетричність будь-яких двох елементів. Відношення R на множині М називається симетричним, якщо для будь-яких 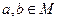 одночасно справедливо
одночасно справедливо 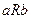 й
й 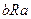 (тобто
(тобто 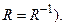 Симетрична паралельність прямих, тому що якщо
Симетрична паралельність прямих, тому що якщо 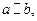 те
те 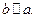 Симетричне відношення «бути рівним» на будь-якій множині або «бути взаємо простим» на
Симетричне відношення «бути рівним» на будь-якій множині або «бути взаємо простим» на 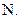
4. Антисиметричність. Якщо для незбіжних елементів 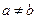 вірне відношення
вірне відношення 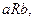 то хибне
то хибне 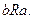 Антисиметричними є відношення «бути більше», «не менше» на
Антисиметричними є відношення «бути більше», «не менше» на 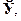 «бути дільником» на
«бути дільником» на 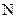 й ін.
й ін.
5. Транзитивність. Якщо 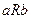 й
й 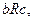 то
то 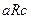 для будь-яких
для будь-яких 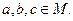 Транзитивні відношення «бути більше», «бути паралельним», «бути рівним» і ін.
Транзитивні відношення «бути більше», «бути паралельним», «бути рівним» і ін.
6. Антитранзитивність. Має місце, коли відношення не має властивість 5. Наприклад, «бути перпендикулярним» на множині прямі площини 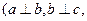 але невірно
але невірно 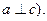
7. Асиметричність. Для жодної пари 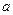 й
й 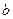 не виконується одночасно
не виконується одночасно 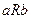 й
й 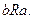
8. Зв’язність. Для будь-яких 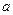 і
і  якщо
якщо 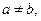 та
та 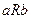 або
або 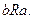
Деяка властивості конкретних бінарних відношень наведені в табл. 1.6.
Розглянемо основні види бінарних відношень.






