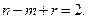В орграфі маршрут є орієнтованим і називається шляхом. На шлях відразу накладають важливі вимоги, що є частиною визначення:
Ø напрямок кожної дуги повинне збігатися з напрямком шляху;
Ø жодне ребро шляху не повинне зустрічатися двічі.
Інакше кажучи, шлях — упорядкована послідовність ребер орієнтованого графа, у якій кінець попереднього ребра збігається з початком наступне й все ребра єдині. Цикл в орграфі — шлях, у якого збігаються початок і кінець. Для циклів орграфа також справедлива теорема про циклічні підстановки. Ланцюг, шлях і цикл у графі називаються простими, якщо вони проходять через кожну з вершин не більше одного разу. Неорієнтований граф називається зв'язковим, якщо між будь-якими двома його вершинами є маршрут. Для зв'язного графа орієнтація дуг не обов'язкова. Так, граф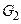 
(рис. 2.1, б) є зв'язковим, а граф 
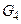(рис. 2.1, г) — незв'язним. Також можна ввести поняття зв’язності для вершин графа: дві вершини називаються зв'язковими, якщо існує маршрут між ними. Зрозуміло, що зв’язність між вершинами є бінарним відношенням. Це відношення буде відношенням еквівалентності. Дійсно, відношення зв’язністі має відомі властивості, тобто воно:
Ø рефлексивне — кожна вершина (включаючи ізольовані) зв'язна сама із собою;
Ø симетричне — будь-який маршрут 
можна представити у зворотному порядку: 
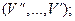
Ø транзитивне — якщо вершина V з'єднана з вершиною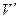 
маршрутом 
а вершина 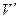з'єднана з вершиною 
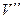маршрутом 
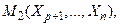то вершина V з'єднана з вершиною 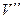маршрутом 
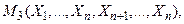у якому спочатку йдуть всі ребра маршруту 
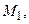а потім всі ребра маршруту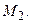 
Граф G можна розбити на непересічні підмножини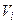 
по ознаці зв’язністі. Вершини однієї множини є зв'язковими між собою, а вершини різних множин — незв'язні. Тоді всі підграфи 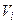(класи еквівалентності) графа G називають зв'язними компонентами, або компонентами зв’язністі. Зв'язний граф має один компонент зв’язності.
Доведено, що в кінцевому зв'язному графі завжди можна побудувати орієнтований цикл, що проходить через кожне ребро по одному разі у двох напрямках. Такий цикл називають способом обходу всього графа й використовують при рішенні багатьох прикладних задач. Зокрема, розроблені спеціальні алгоритми обходу ребер графа, які можна використовувати при рішенні задач виду «пошуку виходу з лабіринту». У лабіринті доріжки служать ребрами графа, а їхнього розгалуження, початок руху (вхід) і кінець (вихід) - вершинами графа. Якщо вхід і вихід належать одному компоненту зв’язністі, то такий лабіринт принципово проходимо, якщо різним - то непрохідний. У другому випадку не допоможе навіть міфологічна «нитка Аріадни».
Теорема 2.3. Для того щоб зв'язний граф G був простим циклом, необхідно й досить, щоб кожна його вершина мала ступінь, рівну 2.
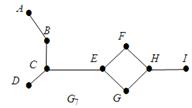
Рис.2.4. Граф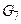 
з мостом CE
Ребро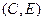 
зв'язного графа G називається мостом, якщо після його видалення G стане незв'язним і розпадеться на два зв'язкових графа 
й 
На рис. 2.4 міст (CЕ)розділив зв'язний граф 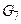на два різних зв'язкових графа: з вершинам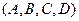и 
й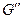 
з вершинами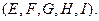 
Теорема 2.4. Ребро графа є мостом тоді й тільки тоді, коли не належить жодному циклу.
Які графи можна вважати різними, а які не розрізняються?
Графи й 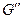називаються ізоморфними, якщо існує взаємо-однозначна відповідність між їхніми ребрами й вершинами, причому відповідні ребра з'єднують відповідні вершини. Оскільки в даному розділі досліджуються кінцеві множини, така бієкція повинна бути підстановкою. Між назвою вершини і її номером розходження немає. Суміжність двох вершин є бінарне відношення, тому ізоморфізм графів можна розглядати як ізоморфізм множин їхніх вершин, на якому уведене відношення суміжності. Отже, графи 
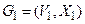і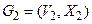 
називаються ізоморфними, якщо 
й існує підстановка 
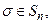така, що 
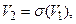а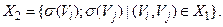 
Іншими словами, можна так перепозначити вершини першого графа, що в нових позначеннях вершини й ребра будуть збігатися із другим графом, причому кратним ребрам першого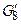 
повинні відповідати кратні ребра другого 
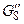такої ж кратності (рис. 2.5).
Аналогічно встановлюється ізоморфізм між орієнтованими графами. При цьому варто пам'ятати, що ребро є впорядкованою множиною, і треба бути особливо уважним, дотримуючись порядку.
Важливо, що ізоморфізм графів є відношенням еквівалентності. Це зручніше за все помітити виходячи із властивостей підстановок. На практиці такі різні по зовнішніх ознаках ізоморфні графи не розрізняють, розглядаючи їх з точністю до ізоморфізму.
Граф G називається планарним (плоским), якщо існує ізоморфний йому граф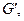 
у зображенні якого на площині ребра перетинаються тільки у вершинах. Іншими словами, у планарного графа ніякі два ребра не мають загальних точок, крім загальних вершин. На рис. 2.1 графи 
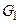і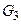 
є планарними, а 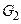— немає. Областю назвемо підмножину площини, що перетинається із планарним графом тільки по деякому простому
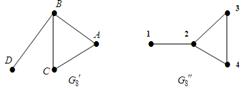
Рис. 2.5. Ізоморфні графи
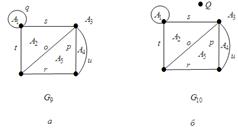
Рис. 2.6. Графи:
а — 
(з областями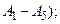 
б —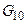 
(з областями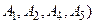 
циклу графа, що є границею області. Оскільки розглядаються кінцеві графи, то плоский граф завжди є обмеженою підмножиною площини. Нехай М — планарний граф із внутрішніми областями. Тоді доповнення М, тобто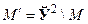 
також може бути областю. Наприклад, граф (рис.2.6, а)виділяє в площині наступні області: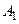 
із границею 
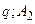із границею 
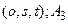із границею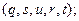 
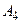із границею 
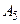із границею 
Множина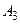 
на рис. 2.6, б)областю не є, тому що перетинання 
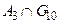містить точку 
не приналежному ніякому циклу.
Теорема 2.5 (Ейлера). Зв'язний плоский граф з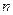 
вершинами й 
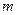ребрами розбиває площину на 
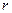областей (включаючи зовнішню), причому
