На откосах от площадки горизонтали параллельны краям площадки, т.к. они тоже являются горизонталями.(Рис.9), а все горизонтали параллельны между собой.
Откос от дороги – это плоскость, касательная к системе конусов, стоящих вдоль бровки (края) дороги и расположенных в точках пересечения горизонталей дороги с бровкой дороги или границей канавки. Дорога имеет уклон, а поэтому горизонтали откосов от нее не будут параллельны ее краям. Конусы, расположенные вдоль кромки дороги, могут быть вершинами вверх или вниз.
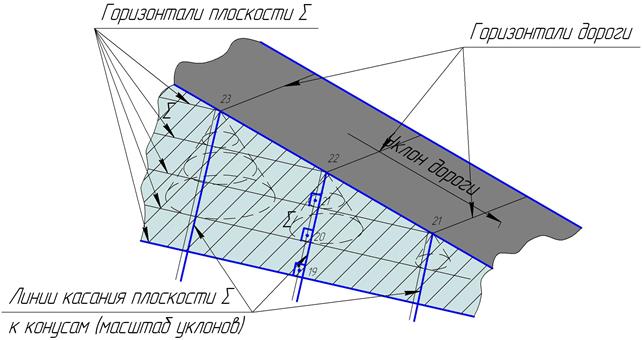
Рис. 14
На рис 14 изображена плоскость Σ касательная к семейству конусов, вершины которых расположены вверх с одним и тем же наклоном образующих к оси вращения. Горизонталь – окружность конуса, расположенная на одну отметку ниже чем вершина, и вершина следующего конуса, расположены на отметку ниже поэтому, имеют одинаковую отметку. Поэтому прямая, проведенная через вершину следующего конуса и касательная к горизонтали – окружности предыдущего конуса есть горизонталь плоскости Σ.
Остальные горизонтали плоскости Σ будут параллельны ей.
На рис. 15 показывается как строятся на чертеже горизонтали плоскости, касательной к конусам. Масштаб уклона ее проводится на любом из конусов

Рис. 15
Для упрощения построения достаточно построить:
а) одну горизонталь.
б) масштаб падения, перпендикулярный ей, с нанесенными интервалами.
в) горизонтали плоскости, проведенные через интервалы и параллельные построенной горизонтали.

Рис. 16
На рис 16 изображена плоскость Σ касательная к семейству конусов, вершины которых расположены вниз и находятся в точках пересечения горизонталей дороги с ее границей. Все конусы с одинаковым наклоном образующих к осям вращения. Вершина каждого последующего конуса на одну отметку больше. Так как горизонталь – окружность предыдущего конуса и вершина следующего конуса имеют одну и ту же отметку, то касательная, проведенная через вершину конуса к окружности – горизонтали, и будет горизонталью плоскости Σ.

Рис. 17
На рис. 17 показано, как строятся горизонтали плоскости Σ на чертеже. Масштаб уклона плоскости откоса проводится из вершины любого конуса перпендикулярно горизонталям (через точки касания горизонталей плоскости с горизонталями конуса).
Задание топографической поверхности
Поверхности, образование которых не подчинено определенным законам, называются каркасными или градоическими поверхностями. Они используются в авиации, судостроении, автостроении и других отраслях техники. К ним относятся и земная поверхность, которую принято называть топографической поверхностью. На чертеже она задается проекциями горизонталей. Горизонтали это линии пересечения топографической поверхности с плоскостями, параллельными плоскости нулевого уровня. Расстояние между плоскостями – 1ед.

Рис. 18 Рис. 19
На рис.18 горизонтали представляют собой замкнутые плоские кривые, по взаимному расположению которых и по отметкам можно судить о рельефе изображаемой местности.
По расстоянию между горизонталями топографической поверхности можно судить об уклоне поверхности в том или ином направлении. Чем меньше расстояния (интервалы) между проекциями смежных горизонталей, тем круче уклоны топографической поверхности и наоборот. Уклоны изображений на чертеже поверхности от точки, имеющей отметку 14, в направлении «а» более пологий, чем в направлении «b». (рис.19)
Если горизонтали местности не замкнутые линии, то числовые отметки ставятся с обеих сторон для удобства построений.






