Проекции с числовыми отметками
Учебно-методическое пособие для выполнения части дисциплины
«Инженерная графика»
«План вертикальной планировки»
Тольятти
ТГУ
2011 г.
УДК
744.4(075.8):624.13(0758)
ББК 30.11я73
П79
Методические указания по курсу «Инженерная графика»
Авторы: Буткова Т.А., Елисеева М.П.
Рецензент Живоглядова И. А.
«Проекции с числовыми отметками» - Учебно-методическое пособие для выполнения части дисциплины «Инженерная графика»
Данные методическое пособие содержат теоретический и практический материал по дисциплине, который поможет студентам выполнить самостоятельную графическую работу, а также контрольную работу по этой же теме.
Эта работа предназначена для студентов строительных специальностей. Она знакомит их с выполнением строительных работ на нулевом уровне.
© ГОУВПО «Тольяттинский государственный университет»
Содержание
1. Введение ………………………………………………………………………4
2. Цели и задачи темы ………………………………………………………......4
3. Сущность метода и проекции точек…………………………………………6
4. Задание на чертеже отрезков прямой………………………………………..7
5. Градуирование прямой ………………………………………………………8
6. Угловой масштаб……………………………………………………………..9
7. Задание на чертеже плоскости……………………………………………...10
8. Построение линий пересечения плоскостей……………………………….12
9. Задание на чертеже прямого кругового конуса……………………………13
10. Построение линии пересечения конической поверхности с плоскостью14
11. Построение горизонталей откосов дороги ………………………………...15
12. Задание топографической поверхности……………………………………18
13. Построение профиля местности……………………………………………19
14. Построение линии пересечения топографической поверхности с плоскостью…………………………………………………………………..20
15. Построение линии пересечения конической поверхности с топографической…………………………………………………………….22
16. Определение нуля работ на площадке и дороге…………………………..23
17. Примеры выполнения чертежей земельных работ на дорогах…………..26
18. Построение промежуточных горизонталей на плане местности………...28
19. Построение сечения сооружения…………………………………………...32
20. Содержание задания…………………………………………………………37
21. Последовательность выполнения задания…………………………………38
22. Оформление чертежа………………………………………………………..47
23. Глоссарий…………………………………………………………………….48
24. Пример выполнения задания………………………………………………..50
25. Литература…………………………………………………………………...51
Введение
В инженерной практике существуют такие объекты, для которых метод проецирования на две и более взаимно перпендикулярные плоскости проекций непригоден: изображения получаются мало наглядными, а точность графических построений на таких чертежах недостаточна при решении позиционных и метрических задач.
В строительном деле такими объектами являются участки земной поверхности с различными сооружениями на ней: строительными площадками, автодорогами, каналами и т.д.
Отличительной чертой таких объектов является значительное преобладание горизонтальных размеров над вертикальными.
Чертежи же, выполненные в проекциях с числовыми отметками, свободны от этих недостатков и поэтому широко используются в строительной практике.
Цель и задачи.
Цель – овладение студентами навыков изображения различных геометрических фигур в проекциях с числовыми отметками после освоения методов проецирования по дисциплине «Начертательная геометрия». Приобретение знаний и умений в составлении и оформлении чертежей.
Задачи – построение однокартинных чертежей на основе метода ортогонального проецирования;
- реконструирование пространства – это умение по однокартинному изображению восстановить оригинал;
- развитие графической культуры
- подготовка к формированию конструктивно – геометрического инженерного мышления;
- формирование у студентов способности к саморазвитию, творческому применению полученных знаний, способам адаптации к профессиональной деятельности;
- грамотно выполнять чертежи;
- воспитание эмоционально-волевых качеств: системность, трудолюбие, внимательность, рефлексии.
В результате изучения темы «План вертикальной планировки» студент должен:
Иметь представление:
О роли данной темы в деятельности будущего инженера строителя;
О методах решения поставленных задач графическими способами;
О правилах оформления чертежей.
Знать:
- основные геометрические понятия;
- методы проецирования геометрических фигур на плоскость чертежа;
- правила решения различных задач на одной плоскости проекций;
- читать однокартинные чертежи;
- правила оформления однокартинных чертежей.
Уметь:
В результате изучения темы «План вертикальной планировки» студент должен:
Иметь представление:
- о роли и месте однокартинных чертежей в инженерной деятельности будущего специалиста строителя;
Уметь:
Решать пространственные задачи на плоскости, т.е. определять по графическому изображению геометрических фигур их положение относительно плоскости проекций;
- решать позиционные задачи на однокартинном чертеже;
- решать метрические задачи на одной плоскости проекций;
- выражать техническую мысль на чертеже.
Овладеть навыками:
- пространственно-образного мышления, т.е. развить способность не только распознавать и создавать образы геометрических фигур, но и оперировать ими:
- работать с методической литературой.
Сущность метода и построения проекций точек.
В методе с числовыми отметками используется ортогональное проецирование на одну горизонтальную плоскость проекций, называемую плоскостью нулевого уровня или основной плоскостью.
Однокартинные чертежи необратимы, но числовая отметка, стоящая возле изображения, дополняет чертеж и показывает на сколько единиц данная фигура удалена от основной плоскости.
Все чертежи с числовыми отметками сопровождаются линейным масштабом.
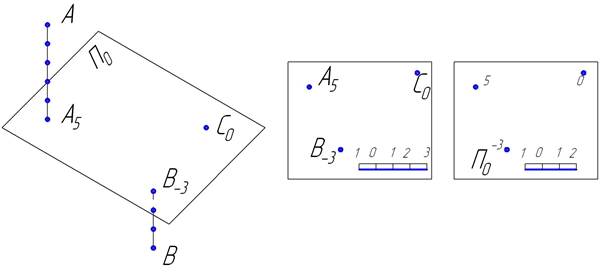
Рис. 1
На рис.1 изображены точки А, В и С. Они ортогонально спроецированы на плоскость проекций П0. Число (отметка), стоящее рядом с буквенным обозначением точки, указывает на сколько единиц (метров) точка удалена от этой плоскости П0. Точка А, расположенная выше плоскости П0, имеет положительную отметку и знак перед числом не ставится.
Точка В, расположенная ниже плоскости нулевого уровня, имеет отрицательную отметку. Знак «-» ставится перед числовой отметкой. Точка С лежит в плоскости П0, поэтому имеет отметку «0».
На чертежах проекции точек можно обозначать буквами с соответствующими числами или одними числами «Рис.1б», если это не затрудняет чтения чертежа.
Такие чертежи с числовыми отметками называют планами. На них обязательно наносится линейный масштаб.
Задание на чертеже отрезка прямой
Прямая может быть задана проекциями любых двух, принадлежащих ей, точек с указанием их отметок. П роекция отрезка прямой называется заложением.(Рис2) Величина заложения отрезка, разность отметок двух точек которого равна единице, называется интервалом и обозначается L. И ли можно сказать, что интервалом прямой является заложение, соответствующее подъему, равному единице. (Рис.2)
Величина заложения зависит от уклона прямой. Эти величины обратные друг другу: чем больше уклон, тем меньше заложение и наоборот. (Рис.3)
Уклон прямой есть отношение алгебраической разности отметок концов отрезка к длине его проекции и обозначается i.
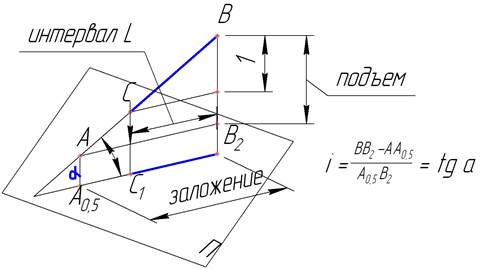
Рис. 2
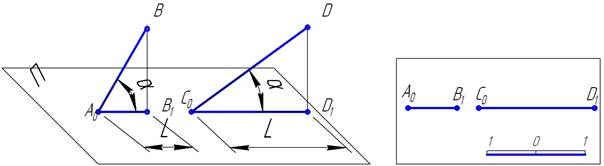
Рис. 3
Градуирование прямой
Проградуировать прямую – значит найти на ней точки, имеющие целочисленные отметки. Например, задан отрезок АВ (А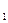 
В 
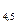). Чтобы проградуировать его, надо на проекции данного отрезка построить проекции точек 2,3,4. Для решения этой задачи применяется метод пропорционального деления отрезка. (Рис.4)
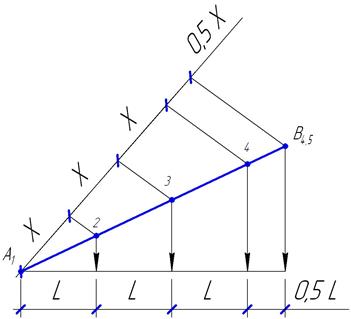
Рис. 4
Из точки А 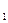(или В 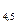) под произвольным углом проводится луч. Так как разность отметок точек А и В составляет 3,5 единицы, то на этом луче откладываем 3 произвольных, но равных отрезка и еще половину такого же отрезка. Последняя засечка соединяется с точкой В 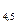. Из всех засечек проводятся прямые, параллельные ему. Этими линиями отрезок А 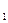В 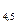делится на такое же количество равных частей. Проставляются отметки точек имеющих целые числа.
Угловой масштаб
Угловой масштаб выполняется для определения интервалов прямых, имеющих разный уклон. Например, задается уклон выемки i в= 3/4, уклон насыпи iн = 1/2 и уклон дороги (подъездных путей) iп.п = 1/5.
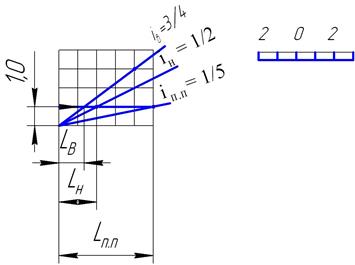
Рис. 5
По заданному линейному масштабу определяется, что величина одной единицы равна 5мм.
Строится сетка, высота и ширина клеточек по 5мм. (Рис.5)
Чтобы построить прямую с уклоном 3/4, откладываем числитель (3 клеточки) на вертикальной линии, а знаменатель (4 клеточки) на горизонтальной. Строим прямоугольник. диагональ этого прямоугольника и есть прямая с уклоном 3/4. На этой прямой находим точку, которая на одну единицу выше самой нижней точки. Проекция этого отрезкаходим точку, которая на одну единицу выше самой нижней точки. горизонтальной.клон.тся интервалом и обозначаетсяй плоскости П. и есть интервал выемки (L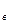 
), остальные интервалы определяются аналогично.
Задание плоскости
В проекциях с числовыми отметками, как и в других методах, плоскость может быть задана тремя точками, не лежащими на одной прямой; прямой и точкой, не лежащей на этой прямой; двумя параллельными или двумя пересекающимися прямыми; плоской фигурой. Однако чаще всего задается масштабом уклонов (масштабом падения) т.к. в проекциях с числовыми отметками такое задание является более наглядным и удобным для решения большинства инженерных задач.
Масштаб уклонов – это проградуированная проекция линии наибольшего ската.(проекция линии ската, на которую нанесены ее интервалы).
Линия наибольшего ската плоскости Р перпендикулярна линии пересечения этой плоскости с плоскостью проекций. А любая линия, лежащая в плоскости Р и параллельная линии пересечения плоскостей, будет горизонтальной. Тогда можно сказать, что линия наибольшего ската есть прямая перпендикулярная горизонталям плоскости. (Рис.6)
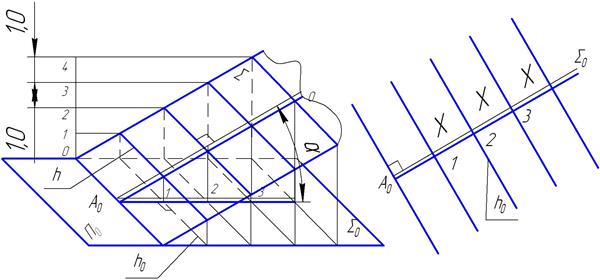
Рис. 6 Рис. 7
Из свойства проецирования прямого угла горизонтальная проекция линии наибольшего ската перпендикулярна горизонтальной проекции горизонтали. Поэтому на плане плоскость задается проекцией линии наибольшего ската (масштабом уклона) с интервалами и проекциями горизонталей, проходящими через них, перпендикулярными проекции линии ската. (Рис.7) Проставляются отметки каждой горизонтали.
Масштабы уклонов на плане проводятся двумя параллельными линиями – одна из них толстая, другая тонкая. Числовые отметки проставляются со стороны толстой линии.
