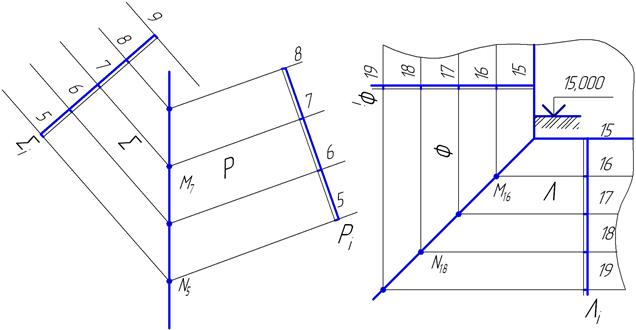
Рис. 8 Рис. 9
На рис. 8 заданы две плоскости Σ и Ρ с разным уклоном: уклон плоскости Σ больше, т.к. интервалы меньше, а уклон Ρ меньше, т.к. интервал больше. Две плоскости пересекаются по прямой линии. Для ее построения достаточно построить две точки. Такими точками будут точки пересечения одноименных горизонталей, т.к. пересекаться могут только те прямые, которые лежат в одной плоскости. Горизонтали, имеющие отметку 7,лежат в одной горизонтальной плоскости, а значит пересекаются (т. М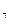 
). Аналогично строится точка N 
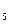. Соединив две точки, принадлежащие обеим плоскостям, получим проекцию линии пересечения.
На рис.9 заданы две плоскости Φ и Λ, имеющие одинаковый уклон, т.к. интервалы их равны, поэтому линия пересечения этих плоскостей будет биссекторной (M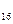 
N 
). Строится она так же, как в предыдущем примере.
Задание прямого кругового конуса
В проекциях с числовыми отметками форма любых поверхностей достаточно полно характеризуется их горизонталями. Все способы представляют собой разновидности каркасного способа задания поверхностей. Для выполнения графической работы достаточно знать, как задается прямой круговой конус и топографическая поверхность.
Если прямой круговой конус пересечь рядом параллельных плоскостей, расположенных перпендикулярно оси вращения, то они пересекут его по концентрическим окружностям-горизонталям. (Рис.10). Если расстояния между плоскостями равны одной единице, то расстояния между окружностями на плане будут равны интервалу.
Таким образом, на чертеже прямой круговой конус задается проекцией образующей снанесенными интервалами (проградуированная проекция образующей), через которые можно провести круговые горизонтали, (рис.11).
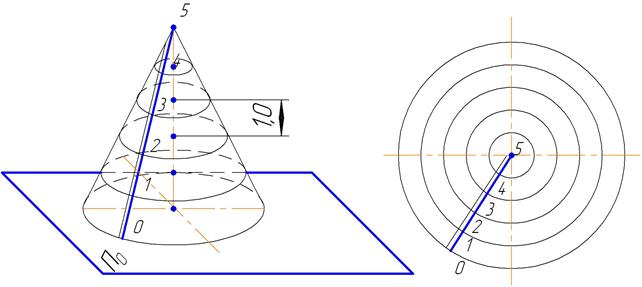
Рис. 10 Рис. 11
Построение линии пересечения конической поверхности с плоскостью.
Коническая поверхность с плоскостью пересекается по плоской кривой линии, которая строится по точкам пересечения горизонталей плоскости с горизонталями конуса с такой же отметкой, т.к. лежат в одной горизонтальной плоскости. (рис.12). Полученные точки соединяются плавной кривой линией. (M 
N 
).
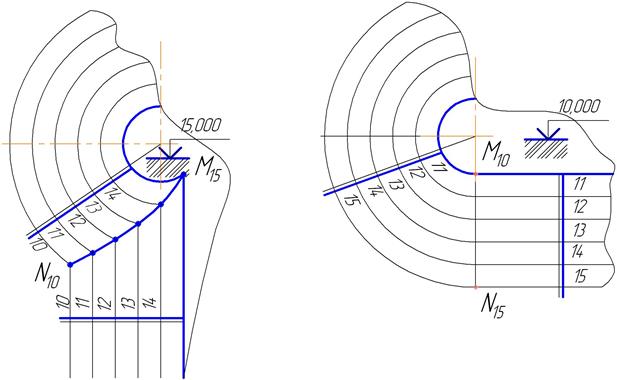
Рис. 12 Рис. 13
На рис.12 прямой круговой конус расположен вершиной вверх, поэтому каждая последующая горизонталь на одну отметку ниже, чем предыдущая. У плоскости точно так же.
На рис. 13 коническая поверхность расположена вершиной вниз и плоскость касательная к ней. Каждая последующая горизонталь на одну отметку выше предыдущей.
Линию касания плоскости выделять не нужно, она остается тонкой сплошной линией. (M 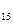N )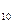
