Линейный коэффициент детерминации. 7 страница

 

Если наиболее высоким оказался коэффициент автокорреляции первого порядка, то исследуемый ряд содержит только:

+ тенденцию;

- циклические колебания с периодичностью в один момент времени;

- сильную нелинейную тенденцию;

- случайную компоненту.

 

Отсутствие автокорреляции в остатках предполагает, что значения ___________ не зависят друг от друга.

+ остатков;

- результата;

- независимых переменных;

- фактора.

 

Коррелограммой называется:

+графическое отображение автокорреляционной функции;

- аналитическое выражение для автокорреляционной функции;

- графическое отображение регрессионной функции;

- процесс экспериментального нахождения значений автокорреляционной функции.

 

Известны значения аддитивной модели временного ряда: 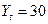- значение уровня ряда, 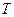=15 - значение тренда, =2 - значение случайной компоненты. Определите значение сезонной компоненты .

- 0;

+ 13;

- 1;

- -1.

 

Может ли ряд содержать только одну из компонент?

- не может, так как временной ряд не содержит компонент, влияющих на его уровни;

+ может, если другие две компоненты не участвуют в формировании уровней ряда;

- может, если он представлен данными, описывающими совокупность различных объектов в определенный момент времени;

- не может, так как уровень ряда должен формироваться под воздействием всех трех компонент.

 

Временной ряд характеризует …

- совокупность последовательных моментов (периодов) времени;

+ данные, описывающие один объект за ряд последовательных моментов (периодов) времени;

- зависимость последовательных моментов (периодов) времени;

- данные, описывающие совокупность различных объектов в определенный момент (период) времени.

 

Значения коэффициента автокорреляции рассчитывается по аналогии с …

- линейным коэффициентом регрессии;

- линейным коэффициентом детерминации;

- нелинейным коэффициентом корреляции;

+ линейным коэффициентом корреляции.

 

«Белым шумом» называется:

+ чисто случайный процесс;

- функциональный процесс;

- неслучайный процесс;

- регрессионный процесс.

 

Основной задачей моделирования временных рядов является …

- исключение уровней из совокупности значений временного ряда;

+ выявление и придание количественного значения каждой из трех компонент;

- исключение значений каждой из трех компонент из уровней ряда;

- добавление новых уравнений к совокупности значений временного ряда.

 

Значения коэффициента автокорреляции второго порядка характеризует связь между:

- исходными уровнями и уровнем второго временного ряда;

- исходными уровнями и уровнями другого ряда, сдвинутыми на 2 момента назад;

- двумя временными рядами;

+ исходными уровнями и уровнями этого же ряда, сдвинутыми на 2 момента времени.

 

При построении модели временного ряда проводится:

- расчет каждого уровня временного ряда;

+ расчет значений компонент для каждого уровня временного ряда;

- расчет средних значений компонент для временного ряда в целом;

- расчет последующих и предыдущих значений уровней временного ряда.

 

Стационарность временного ряда означает отсутствие …

+ тренда;

- наблюдений по уровням временного ряда;

- значений уровней ряда;

- временной характеристики.

 

Структуру временного ряда можно выявить с помощью коэффициента …

+ автокорреляции уровней ряда;

- авторегрессии уровней ряда;

- регрессии уровней ряда;

- автодетерминации уровней ряда.

 

Модель временного ряда предполагает …

- независимость значений экономического показателя от времени;

- пренебрежение временными характеристиками ряда;

+ зависимость значений экономического показателя от времени;

- отсутствие последовательности моментов (периодов) времени, в течении которых рассматривается поведение экономического показателя.

 

Стационарность временного ряда не подразумевает отсутствие …

- сезонных колебаний;

- стохастического процесса с наличием тренда;

+ стационарного стохастического процесса;

- конъюнктурных сдвигов.

 

Если наиболее высоким оказался коэффициент автокорреляции третьего порядка, то исследуемый ряд содержит …

+ сезонные колебания с периодичностью в три момента времени;

- линейный тренд, проявляющийся в каждом третьем уровне ряда;

- случайную величину, влияющую на каждый третий уровень ряда;

- нелинейную тенденцию полинома третьего порядка.

 

Если факторы входят в модель как сумма, то модель называется:

- суммарной;

- мультипликативной;

+ аддитивной;

- производной..

 

Экономические временные ряды, представляющие собой данные наблюдений за ряд лет, как правило, являются …

- стационарными временными рядами;

+ функционально зависящими от времени временными рядами;

- строго возрастающими временными рядами;

- нестационарными временными рядами.

 

Значения коэффициента автокорреляции первого порядка равно 0,9. Следовательно …

- линейная связь между последующим и предыдущим уровнями не тесная;

+ линейная связь между последующим и предыдущим уровнями тесная;

- нелинейная связь между последующим и предыдущим уровнями тесная;

- линейная связь между временными рядами двух экономических показателей тесная.

 

Под лагом подразумевается число …

+ периодов, по которым рассчитывается коэффициент автокорреляции;

- уровней исходного временного ряда;

- пар значений, по которым рассчитывается коэффициент автокорреляции;

- уровней ряда, сдвинутых при расчете коэффициента автокорреляции.

 

Стационарность характерна для временного ряда:

- с положительной динамикой роста;

- с отрицательной динамикой роста;

- содержащего сезонные колебания;

+ типа «белый шум».

 

При моделировании временных рядов экономических показателей необходимо учитывать …

- конструктивный характер уровней исследуемых показателей;

+ стохастический характер уровней исследуемых показателей;

- функциональный характер уровней исследуемых показателей;

- не зависящий от времени уровень исследуемых показателей.

 

Модель временного ряда не предполагает …

- зависимость значений экономического показателя от времени;

+ независимость значений экономического показателя от времени;

- учет временных характеристик;

- последовательность моментов (периодов) времени, в течении которых рассматривается поведение экономического показателя.

 

Уровнем временного ряда является …

+ значение временного ряда в конкретный момент (период) времени;

- среднее значение временного ряда;

- совокупность значений временного ряда;

- значение конкретного момента (периода) времени.

 

Параметры уравнения тренда определяются ________методом наименьших квадратов

+ обычным;

- двухшаговым;

- обобщенным;

- косвенным.

 

Максимальный лаг связан с числом уровней временного ряда 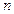следующим соотношением не более …

- ;

+ ;

- ;

- .

 

 

Тема Модели временных рядов (Задачи)

 

На основе помесячных данных за последние 6 лет была построена аддитивная модель временного потребления тепла. Скорректированные значения сезонной компоненты приведены в таблице:

Уравнение тренда выглядит так:

Значение сезонной компоненты за март, а также точечный прогноз потребления тепла на 1 квартал следующего года равны:

+—9; 1290,4

— –9; 1290,4

—9; 1226,4

—12; 1226,4

 

 

На основе помесячных данных за последние 5 лет была построена аддитивная модель временного потребления тепла. Скорректированные значения сезонной компоненты приведены в таблице:

Январь	+ 17	май	- 20	сентябрь	- 10
февраль	+ 15	июнь	- 34	октябрь	?
март	+ 10	июль	- 42	ноябрь	+22
апрель	- 4	август	- 18	декабрь	+27

Уравнение тренда выглядит так:

Значение сезонной компоненты за октябрь, а также точечный прогноз потребления тепла на 1 квартал следующего года равны:

+—37; 1615

—–37; 1615,2

—37; 1845

—4; 1845

 

На основе помесячных данных за последние 8 лет была построена аддитивная модель временного потребления тепла. Скорректированные значения сезонной компоненты приведены в таблице:

Январь	+ 42	Май	- 10	сентябрь	- 10
февраль	+ 21	Июнь	- 50	октябрь	+ 12
март	?	Июль	- 35	ноябрь	+22
апрель	- 1	Август	- 16	декабрь	+28

Уравнение тренда выглядит так:

Значение сезонной компоненты за март, а также точечный прогноз потребления тепла на 1 квартал следующего года равны:

+—-3; 1611,6

—3; 1617,6

—3; 1526,4

—7; 1226,4

 

На основе поквартальных данных построена мультипликативная модель некоторого временного ряда. Скорректированные значения сезонной компоненты равны:

I квартал – 1,6

II квартал – 0,8

III квартал – 0,7

IV квартал -?

Уравнение тренда имеет вид:

Значение сезонной компоненты за IV квартал и прогноз на II и III кварталы следующего года равны:

+—0,90; 5,28 и 4,55

—1,00; 10,72 и 5,28

—0,90; 4,55 и 5,28

—0,80; 5,28 и 10,72

 

На основе поквартальных данных построена мультипликативная модель некоторого временного ряда. Скорректированные значения сезонной компоненты равны:

I квартал – 1,5

II квартал –?

III квартал – 0,6

IV квартал – 0,8

Уравнение тренда имеет вид:

Значение сезонной компоненты за II квартал и прогноз на II и III кварталы следующего года равны:

+—1,10; 16,06 и 8,82

—1,20; 21,75 и 16,06

—1,10; 8,82 и 16,06

—1,00; 16,06 и 21,75

 

На основе поквартальных данных построена мультипликативная модель некоторого временного ряда. Скорректированные значения сезонной компоненты равны:

I квартал – 1,2

II квартал – 0,8

III квартал –?

IV квартал – 1,4

Уравнение тренда имеет вид:

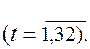
Значение сезонной компоненты за III квартал и прогноз на II и III кварталы следующего года равны:

+—0,60; 4,32 и 3,12

—0,70; 6,72 и 4,32

—0,60; 3,12 и 4,32

—0,50; 4,32 и 6,72

 

На основе поквартальных данных построена мультипликативная модель некоторого временного ряда. Скорректированные значения сезонной компоненты равны:

I квартал – 1,2

II квартал – 0,9

III квартал – 0,5

IV квартал -?

Уравнение тренда имеет вид:

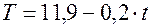
Значение сезонной компоненты за IV квартал и прогноз на II и III кварталы следующего года равны:

+—1,40; 1,71 и 0,85

—1,60; 7,48 и 4,57

—1,40; 1,36 и 4,57

—1,30; 2,28 и 7,48

 

На основе поквартальных данных построена мультипликативная модель некоторого временного ряда. Скорректированные значения сезонной компоненты равны:

I квартал – 1,5

II квартал – 0,7

III квартал –?

IV квартал – 1,2

Уравнение тренда имеет вид:

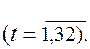
Значение сезонной компоненты за III квартал и прогноз на II и III кварталы следующего года равны:

+—0,60; 4,55 и 3,78

—0,70; 6,72 и 4,55

—0,60; 3,78 и 4,55

—0,50; 4,55 и 6,72

 

На основе квартальных данных объемов продаж 1995 – 2000гг. была построена аддитивная модель временного ряда. Трендовая компонента имеет вид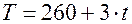

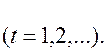
Показатели за 2000 г. приведены в таблице:

Квартал	Фактический объем продаж	Компонента аддитивной модели
трендовая	сезонная	случайная
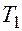
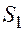
				-9
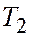
				+4
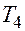
ИТОГО:

Отдельные недостающие данные в таблице равны:

+—

—

—

—

 

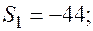
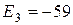
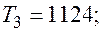
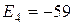
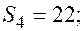
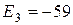
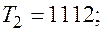
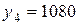
На основе квартальных данных объемов продаж 1995 – 2000гг. была построена аддитивная модель временного ряда. Трендовая компонента имеет вид

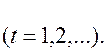
Показатели за 1999 г. приведены в таблице:

Квартал	Фактический объем продаж	Компонента аддитивной модели
трендовая	сезонная	случайная
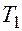
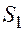
				-11
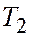
				+5
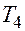
Итого

Отдельные недостающие данные в таблице равны:

+—

—

—

—

 

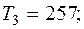
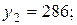
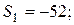
На основе квартальных данных объемов продаж 1995 – 2000гг. была построена аддитивная модель временного ряда. Трендовая компонента имеет вид

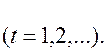
Показатели за 1999 г. приведены в таблице:

Квартал	Фактический объем продаж	Компонента аддитивной модели
трендовая	сезонная	случайная
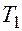
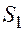
				-11
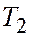
				+5
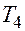
ИТОГО

Отдельные недостающие данные в таблице равны:

+—

—

—

—

 

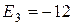
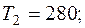
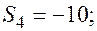
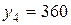
На основе квартальных данных объемов продаж 1995 – 2000гг. была построена аддитивная модель временного ряда. Трендовая компонента имеет вид

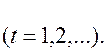
Показатели за 1999 г. приведены в таблице:

Квартал	Фактический объем продаж	Компонента аддитивной модели
трендовая	сезонная	случайная
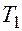
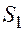
				-11
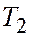
				+5
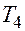
ИТОГО

Отдельные недостающие данные в таблице равны:

+—

—

—

—

 

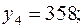
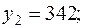
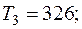
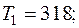
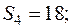
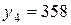
На основе квартальных данных объемов продаж 1996 – 2000гг. была построена аддитивная модель временного ряда. Трендовая компонента имеет вид

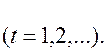
Показатели за 1999 г. приведены в таблице:

Квартал	Фактический объем продаж	Компонента аддитивной модели
трендовая	сезонная	случайная
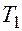
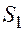
				-10
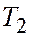
				+3
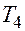
ИТОГО:

Отдельные недостающие данные в таблице равны:

+—

—
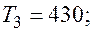