—Наибольшее влияние на результат оказывает фактор 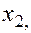 наименьшее -
наименьшее - 


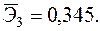
—Наибольшее влияние на результат оказывает фактор  наименьшее -
наименьшее - 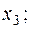

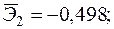

Уравнение регрессии в стандартизованном виде имеет вид:


Как влияют факторы на результат и каковы значения частных коэффициентов эластичности?
+—Наибольшее влияние на результат оказывает фактор 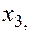 , наименьшее
, наименьшее 



—Наибольшее влияние на результат оказывает фактор 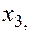 наименьшее -
наименьшее - 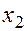 ;
; 


—Наибольшее влияние на результат оказывает фактор 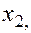 наименьшее -
наименьшее - 


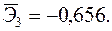
—Наибольшее влияние на результат оказывает фактор  наименьшее -
наименьшее - 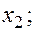
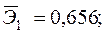


По 20 наблюдениям получены следующие данные:
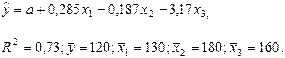
Значения скорректированного коэффициента детерминации, частных коэффициентов эластичности и параметра 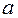 равны:
равны:
+— 
— 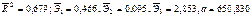
— 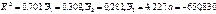
— 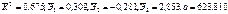
По 16 наблюдениям получены следующие данные:
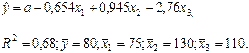
Значения скорректированного коэффициента детерминации, частных коэффициентов эластичности и параметра 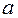 равны:
равны:
+— 
— 
— 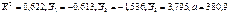
— 





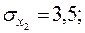


 Уравнения регрессии
Уравнения регрессии  на
на  и
и 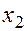 в стандартизованном и натуральном масштабе имеют вид:
в стандартизованном и натуральном масштабе имеют вид:
+— 

— 

— 

— 
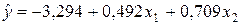





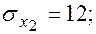


 Уравнения регрессии y на
Уравнения регрессии y на  и
и 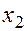 в стандартизированном и натуральном масштабе имеют вид:
в стандартизированном и натуральном масштабе имеют вид:
+— 

— 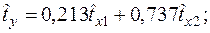
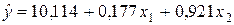
— 

— 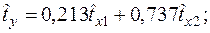









 Уравнения регрессии
Уравнения регрессии  на
на  и
и 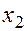 в стандартизованном и натуральном масштабе имеют вид:
в стандартизованном и натуральном масштабе имеют вид:
+— 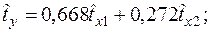

— 

— 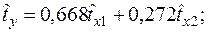

— 
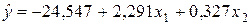

 . Уравнения регрессии в стандартизированном и натуральном масштабе имеют вид:
. Уравнения регрессии в стандартизированном и натуральном масштабе имеют вид:
+— 
— 
— 
— 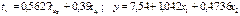

 . Уравнения регрессии в стандартизированном и натуральном масштабе имеют вид:
. Уравнения регрессии в стандартизированном и натуральном масштабе имеют вид:
+— 
— 
— 
— 

 . Уравнения регрессии в стандартизированном и натуральном масштабе имеют вид:
. Уравнения регрессии в стандартизированном и натуральном масштабе имеют вид:
+— 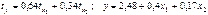
— 
— 
— 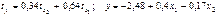

 .Уравнения регрессии в стандартизированном и натуральном масштабе имеют вид:
.Уравнения регрессии в стандартизированном и натуральном масштабе имеют вид:
+— 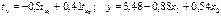
— 
— 
— 
При построении регрессионной зависимости некоторого результативного признака на 8 факторов по 25 измерениям коэффициент детерминации составил 0,736. После исключения 3 факторов коэффициент детерминации уменьшился до 0,584. Обоснованно ли было принятое решение на уровнях значимости 0,1, 0,05 и 0,01:
+—Да, только на уровнях 0,05 и 0,01
—Да, на всех уровнях значимости
—Нет, на всех уровнях значимости
—Да, только на уровне 0,01
—Да, только на уровнях 0,1 и 0,05
При построении регрессионной зависимости некоторого результативного признака на 7 факторов по 32 измерениям коэффициент детерминации составил 0,812. После исключения 2 факторов коэффициент детерминации уменьшился до 0,76. Обоснованно ли было принятое решение на уровнях значимости 0,1, 0,05 и 0,01:
+—Да, только на уровнях 0,05 и 0,01
—Да, на всех уровнях значимости
—Нет, на всех уровнях значимости
—Да, только на уровне 0,01
—Да, только на уровнях 0,1 и 0,05
При построении регрессионной зависимости некоторого результативного признака на 10 факторов по 45 измерениям коэффициент детерминации составил 0,617. После исключения 3 факторов коэффициент детерминации уменьшился до 0,512. Обоснованно ли было принятое решение на уровнях значимости 0,1, 0,05 и 0,01:
+—Да, только на уровне 0,01
—Да, на всех уровнях значимости
—Нет, на всех уровнях значимости
—Да, только на уровнях 0,05 и 0,01
—Да, только на уровнях 0,1 и 0,05
При построении регрессионной зависимости некоторого результативного признака на 10 факторов по 45 измерениям коэффициент детерминации составил 0,347. После добавления 3 факторов коэффициент детерминации увеличился до 0,536. Обоснованно ли было принятое решение на уровнях значимости 0,1, 0,05 и 0,01:
+—Да, на всех уровнях значимости
—Нет, на всех уровнях значимости
—Да, только на уровнях 0,1 и 0,05
—Да, только на уровне 0,1
—Да, только на уровнях 0,05 и 0,01
При построении регрессионной зависимости некоторого результативного признака на 7 факторов по 42 измерениям коэффициент детерминации составил 0,443. После добавления 3 факторов коэффициент детерминации увеличился до 0,527. Обоснованно ли было принятое решение на уровнях значимости 0,1, 0,05 и 0,01:
+—Нет, на всех уровнях значимости
—Да, на всех уровнях значимости
—Да, только на уровнях 0,1 и 0,05
—Да, только на уровне 0,1
—Да, только на уровнях 0,05 и 0,01
При построении регрессионной зависимости некоторого результативного признака на 8 факторов по 38 измерениям коэффициент детерминации составил 0,558. После добавления 2 факторов коэффициент детерминации увеличился до 0,644. Обоснованно ли было принятое решение на уровнях значимости 0,1, 0,05 и 0,01:
+—Да, только на уровнях 0,1 и 0,05
—Да, на всех уровнях значимости
—Нет, на всех уровнях значимости
—Да, только на уровне 0,1
—Да, только на уровнях 0,05 и 0,01
По данным 150 наблюдений о доходе индивидуума Y, уровне его образования X1, и возрасте X2 определите, можно ли считать на уровне значимости 5 % линейную регрессионную модель Y на X1 и X2 гетероскедастичной, если суммы квадратов остатков после упорядочения данных по уровню образования следующие: RSS1 (для 50 значений с наименьшим уровнем образования) = 894,1; RSS2 (для 50 значений с наибольшим уровнем образования) = 3918,2:
+—гипотеза об отсутствии гетероскедастичности отвергается
—гипотеза об отсутствии гетероскедастичности принимается
—на основе имеющихся данных такую гипотезу нельзя проверить
Имеется следующая модель, построенная на основе 30 наблюдений:
Y = 1, 48+ 0, 788X R2 = 0,97
(3,29) (29,37)
В скобках указаны t – статистики
Для проверки гетероскедастичности, были построены отдельные модели по первым 12 и последним 12 наблюдениям. Остаточные суммы квадратов отклонений составили RSS1 = 1069 и RSS2 = 3344. Проверить гипотезу о гомоскедастичности с уровнем значимости 5%:
+—гипотеза о гомоскедастичности отвергается
—гипотеза о гомоскедастичности принимается
—для проверки данной гипотезы в данной задаче недостаточно данных
Имеется следующая модель, построенная на основе 30 наблюдений:
Y = 1, 75+ 1, 251X R2 = 0,97
(3,02) (2,37)
В скобках указаны t – статистики
Для проверки гетероскедастичности, были построены отдельные модели по первым 12 и последним 12 наблюдениям. Остаточные суммы квадратов отклонений составили RSS1 = 344 и RSS2 = 769. Проверить гипотезу о гомоскедастичности с уровнем значимости 5%:
—гипотеза о гомоскедастичности отвергается
+—гипотеза о гомоскедастичности принимается
—для проверки данной гипотезы в данной задаче недостаточно данных
Тема Модели временных рядов (Теоретические вопросы)
Уровень временного ряда может содержать:
—тенденцию, циклические, сезонные колебания, случайные колебания
—тенденцию и сезонные колебания
—сезонные и случайные колебания
+—любое сочетание тенденции, циклических, сезонных, случайных колебаний
Аддитивная модель временного ряда имеет вид:
+— 
— 
— 
Автокорреляцией уравнений временного ряда называют:
+—автокорреляционную зависимость между последовательными уровнями временного ряда
—значение аналитической функции, характеризующей зависимость уровней ряда от времени
—значение перехода
Автокорреляционная функция временного ряда – это:
+—последовательность коэффициентов автокорреляции уровней временного ряда
—коррелограмма
—последовательность уровней временного ряда
Наиболее высокий коэффициента автокорреляции первого порядка свидетельствует о том, что:
+—исследуемый ряд содержит только тенденцию
—исследуемый ряд содержит циклические колебания
—ряд не содержит тенденции и циклических колебаний
Если ни один из коэффициентов автокорреляции не является значимым, это свидетельствует о том, что:
—исследуемый ряд содержит только тенденцию
—исследуемый ряд содержит циклические колебания
+—временный ряд не содержит тенденции и циклических колебаний
Кусочно – линейная модель регрессии применяется:
+—для моделирования тенденции временного ряда, испытывающего влияние структурных изменений
—для моделирования тенденции временного ряда за небольшой промежуток времени
—для моделирования тенденции временного ряда
Коинтеграция временных рядов:
+—причинно – следственная зависимость в уровнях двух (или более) временных рядов
—корреляционная зависимость между последовательными уровнями временного ряда
—последовательность коэффициентов автокорреляции уровней временного ряда
Авторегрессионные модели включают в качестве объясняющих переменных:
+—лаговые значения зависимых переменных
—лаговые значения независимых переменных
—лаговые значения зависимых и независимых переменных
Модели с распределенными лагами включают в качестве объясняющих переменных:
—лаговые значения зависимых переменных
+—лаговые значения независимых переменных
—лаговые значения зависимых и независимых переменных
Суть метода инструментальных переменных состоит в:
+—замене переменной модели на новую переменную, которая тесно коррелирует с прежней, но не коррелирует с остатками модели
—замене переменной модели на новую переменную, которая тесно коррелирует с остатками модели, но не коррелирует с прежней переменной
—в упрощении модели
Дополнительные вопросы
«Белым шумом» называется:
+ чисто случайный процесс;
- функциональный процесс;
- неслучайный процесс;
- регрессионный процесс
Проверка является ли временной ряд «белым шумом» осуществляется с помощью:
+  статистики Бокса-Пирса;
статистики Бокса-Пирса;
- величины лага;
- критерия Дарбина-Уотсона;
- коэффициента автокорреляции.
Значения коэффициента автокорреляции первого порядка равно 0,9. Следовательно …
- линейная связь между последующим и предыдущим уровнями не тесная;
+ линейная связь между последующим и предыдущим уровнями тесная;
- нелинейная связь между последующим и предыдущим уровнями тесная;
- линейная связь между временными рядами двух экономических показателей тесная.
Параметры уравнения тренда определяются ________методом наименьших квадратов
+ обычным;
- двухшаговым;
- обобщенным;
- косвенным.
Стационарность временного ряда означает отсутствие …
+ тренда;
- наблюдений по уровням временного ряда;
- значений уровней ряда;
- временной характеристики.
Модель временного ряда не предполагает …
- зависимость значений экономического показателя от времени;
+ независимость значений экономического показателя от времени;
- учет временных характеристик;
- последовательность моментов (периодов) времени, в течении которых рассматривается поведение экономического показателя.
Временной ряд называется стационарным, если он является реализацией _____________ процесса:
- функционального;
+ стационарного стохастического;
- нестационарного стохастического;
- неслучайного.
Временной ряд – это совокупность значений экономического показателя....
- за несколько непоследовательных моментов (периодов) времени;
- независящих от времени;
- по однотипным объектам;
+ за несколько последовательных моментов (периодов) времени.
Построена мультипликативная модель временного ряда, где 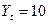 - значение уровня ряда,
- значение уровня ряда, 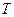 - значение тренда,
- значение тренда,  - значение сезонной компоненты,
- значение сезонной компоненты,  - значение случайной компоненты. Определите вариант правильного найденных значений компонент уровней ряда:
- значение случайной компоненты. Определите вариант правильного найденных значений компонент уровней ряда:
-  ;
;
+  ;
;
-  ;
;
- 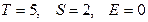 .
.
Временной ряд – это совокупность значений экономического показателя....
- за несколько непоследовательных моментов (периодов) времени;
- независящих от времени;
- по однотипным объектам;
+ за несколько последовательных моментов (периодов) времени.
Построена мультипликативная модель временного ряда, где 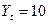 - значение уровня ряда,
- значение уровня ряда, 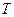 - значение тренда,
- значение тренда,  - значение сезонной компоненты,
- значение сезонной компоненты,  - значение случайной компоненты. Определите вариант правильного найденных значений компонент уровней ряда:
- значение случайной компоненты. Определите вариант правильного найденных значений компонент уровней ряда:
-  ;
;
+  ;
;
-  ;
;
- 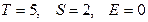 .
.
Временной ряд называется стационарным, если он является реализацией _____________ процесса:
- функционального;
+ стационарного стохастического;
- нестационарного стохастического;
- неслучайного.
Проверка является ли временной ряд «белым шумом» осуществляется с помощью:
+  статистики Бокса-Пирса;
статистики Бокса-Пирса;
- величины лага;
- критерия Дарбина-Уотсона;
- коэффициента автокорреляции.
В общем случае каждый уровень временного ряда формируется под воздействием …
- случайных временных воздействий;
- сезонных колебаний и случайных факторов;
+тенденции, сезонных колебаний и случайных факторов;
- тенденции и случайных факторов.
Под стационарным процессом можно понимать …
- процесс с возрастающей тенденцией;
- процесс с убывающей тенденцией;
+ стохастический процесс, для которого среднее и дисперсия независимо от рассматриваемого периода имеют постоянные значения;
- функциональный процесс.
Автокорреляционной функцией временного ряда называется:
- последовательность приращений коэффициентов автокорреляции уровней различных порядков;
- последовательность отношений коэффициентов автокорреляции к величинам соответствующих лагов;
- зависимость коэффициентов автокорреляции первого порядка от числа уровней временного ряда;
+ последовательность значений коэффициентов автокорреляции различных порядков.
Известны значения мультипликативной модели временного ряда:  - значение уровня ряда,
- значение уровня ряда, 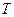 =5 - значение тренда,
=5 - значение тренда,  =3 - значение сезонной компоненты. Определите значение компоненты
=3 - значение сезонной компоненты. Определите значение компоненты  (случайной компоненты).
(случайной компоненты).
-  = -1;
= -1;
-  =3;
=3;
+  =1;
=1;
-  =0.
=0.
Мультипликативная модель содержит исследуемые факторы …
- в виде их отношений;
- в виде слагаемых;
+ в виде сомножителей;
- в виде комбинации слагаемых и сомножителей.
Уровень временного ряда может формироваться под воздействием тенденции, сезонных колебаний и …
- динамической составляющей;
- тренда;
- циклических колебаний;
+ случайных воздействий.
Циклические колебания связаны с …
- трендовыми взаимодействиями между экономическими показателями;
- общей динамикой конъюнктуры рынка;
- воздействием аномальных факторов;
+ сезонностью некоторых видов экономической деятельности (сельское хозяйство, туризм и.т.д.).






