Для двух видов продукции А и Б зависимость удельных постоянных расходов от объема выпускаемой продукции выглядят следующим образом:
Сравнить эластичности затрат по каждому виду продукции при x=80 и определить объем выпускаемой продукции обоих видов, при котором их эластичность будут одинаковы
+— 
— 
— 
— 
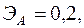
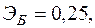
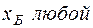
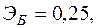
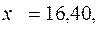
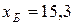
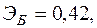
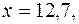
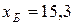
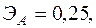
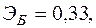
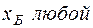
Для двух видов продукции А и Б зависимость удельных постоянных расходов от объема выпускаемой продукции выглядят следующим образом:
Сравнить эластичности затрат по каждому виду продукции при x=40 и определить объем выпускаемой продукции обоих видов, при котором их эластичность будут одинаковы
+— 
— 
— 
— 
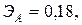
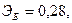
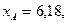
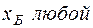
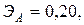
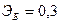
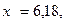
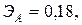
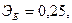
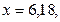
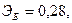
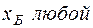
Для двух видов продукции А и Б зависимость удельных постоянных расходов от объема выпускаемой продукции выглядят следующим образом:
Сравнить эластичности затрат по каждому виду продукции при x=25 и определить объем выпускаемой продукции обоих видов, при котором их эластичность будут одинаковы
+— 
— 
— 
— 
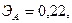
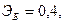
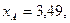
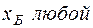
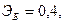
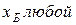
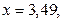
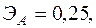
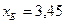
Для двух видов продукции А и Б зависимость удельных постоянных расходов от объема выпускаемой продукции выглядят следующим образом:
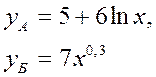
Сравнить эластичности затрат по каждому виду продукции при x=30 и определить объем выпускаемой продукции обоих видов, при котором их эластичность будут одинаковы
+— 
— 
— 
— 
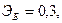
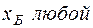
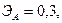
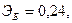
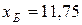
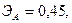
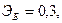
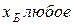
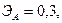
Для двух видов продукции А и Б зависимость удельных постоянных расходов от объема выпускаемой продукции выглядят следующим образом:
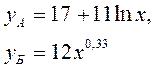
Сравнить эластичности затрат по каждому виду продукции при x=40 и определить объем выпускаемой продукции обоих видов, при котором их эластичность будут одинаковы
+— 
— 
— 
— 
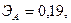
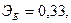
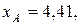
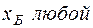
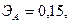
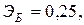
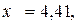
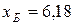
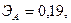
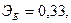
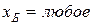
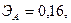
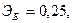
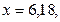
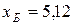
Для двух видов продукции А и Б зависимость удельных постоянных расходов от объема выпускаемой продукции выглядят следующим образом:
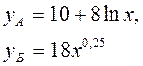
Сравнить эластичности затрат по каждому виду продукции при x=45 и определить объем выпускаемой продукции обоих видов, при котором их эластичность будут одинаковы
+— 
— 
— 
— 
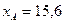
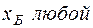
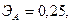
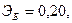
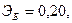
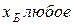
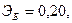
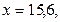
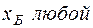
Для двух видов продукции А и Б зависимость удельных постоянных расходов от объема выпускаемой продукции выглядят следующим образом:
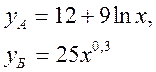
Сравнить эластичности затрат по каждому виду продукции при x=40 и определить объем выпускаемой продукции обоих видов, при котором их эластичность будут одинаковы
— 
— 
— 
+— 
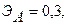
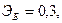
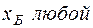
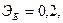
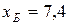
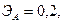
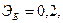
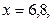
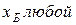
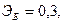
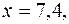
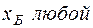
Для двух видов продукции А и Б зависимость удельных постоянных расходов от объема выпускаемой продукции выглядят следующим образом:
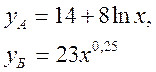
Сравнить эластичности затрат по каждому виду продукции при x=55 и определить объем выпускаемой продукции обоих видов, при котором их эластичность будут одинаковы
+— 
— 
— 
— 
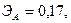
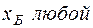
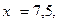
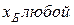
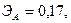
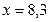
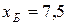
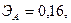
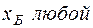
Пусть имеется уравнение парной регрессии:
построенное по 15 наблюдениям. При этом r=-0.7. Доверительный интервал для коэффициента регрессии в этой модели имеет вид:
+—(-11,11; -0,89) с вероятностью 0,99
—(-9,67;-2,33) с вероятностью 0,99
—(-9,01; -2,99) с вероятностью 0,95
—(-8,53; -2,32) с вероятностью 0,9
Пусть имеется уравнение парной регрессии:
построенное по 18 наблюдениям. При этом r=-0.75. Доверительный интервал для коэффициента регрессии в этой модели имеет вид:
+—(-6,92; -3,08) с вероятностью 0,9
—(-6,92;-3,08) с вероятностью 0,95
—(-8,22; -1,78) с вероятностью 0,95
—(-7,34; -2,66) с вероятностью 0,99
Пусть имеется уравнение парной регрессии:
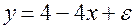
построенное по 20 наблюдениям. При этом r=-0.65. Доверительный интервал для коэффициента регрессии в этой модели имеет вид:
+—(-6,32;-1,68) с вероятностью 0,95
—(-5,91;-2,09) с вероятностью 0,99
—(-6,32; -1,68) с вероятностью 0,99
—(-5,91; -2,09) с вероятностью 0,95
Пусть имеется уравнение парной регрессии:
построенное по 22 наблюдениям. При этом r=0.73. Доверительный интервал для коэффициента регрессии в этой модели имеет вид:
+—(1,69; 4,31) с вероятностью 0,95
—(-0,49;6,49) с вероятностью 0,95
—(-1,76; 7,76) с вероятностью 0,99
—(1,23; 4,77) с вероятностью 0,99
Пусть имеется уравнение парной регрессии:
построенное по 24 наблюдениям. При этом r=0.68. Доверительный интервал для коэффициента регрессии в этой модели имеет вид:
+—(2,46;11,54) с вероятностью 0,99
—(2,50; 11,50) с вероятностью 0,99
—(6,36; 7,64) с вероятностью 0,90
—(3,68; 10,32) с вероятностью 0,95
Пусть имеется уравнение парной регрессии:
построенное по 20 наблюдениям. При этом r=0.86. Доверительный интервал для коэффициента регрессии в этой модели имеет вид:
+—(2,27;3,73) с вероятностью 0,90
—(2,14;3,86) с вероятностью 0,95
—(2,28; 3,72) с вероятностью 0,99
—(1,85; 4,15) с вероятностью 0,99
Пусть имеется уравнение парной регрессии:
построенное по 15 наблюдениям. При этом r=0,53. Доверительный интервал для коэффициента регрессии в этой модели имеет вид:
+—(0,20;9,80) с вероятностью 0,95
—(0,05;9,95) с вероятностью 0,99
—(1,17; 8,83) с вероятностью 0,90
—(0,35; 9,65) с вероятностью 0,95
Пусть имеется уравнение парной регрессии:
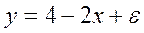
построенное по 18 наблюдениям. При этом r=-0,6. Доверительный интервал для коэффициента регрессии в этой модели имеет вид:
+—(-3,42;-0,58) с вероятностью 0,95
—(-3,7;-0,3) с вероятностью 0,99
—(-3,21; -0,79) с вероятностью 0,90
—(-3,56; -0,44) с вероятностью 0,95
Пусть имеется уравнение парной регрессии:
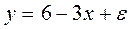
построенное по 16 наблюдениям. При этом r= 
. Доверительный интервал для коэффициента регрессии в этой модели имеет вид:
+—(-4,80;-1,2) с вероятностью 0,99
—(-4,36;-1,64) с вероятностью 0,95
—(-3,98; -2,02) с вероятностью 0,90
—(-4,96; -1,04) с вероятностью 0,99
Пусть имеется уравнение парной регрессии:
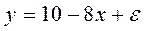
построенное по 14 наблюдениям. При этом 
. Доверительный интервал для коэффициента регрессии в этой модели имеет вид:
+—(-16,72; 0,72) с вероятностью 0,95
—(-17,32; 1,32) с вероятностью 0,99
—(-16,13; 0,13) с вероятностью 0,90
—(-15,76; -0,24) с вероятностью 0,90
Уравнение регрессии потребления материалов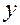 
от объема производства 
, построенное по 18 наблюдениям, имеет вид:
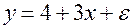
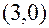
В скобках – фактическое значение t – критерия. Коэффициент детерминации для этого уравнения равен:
+—0,360
—0,384
—0,247
—0,456
Уравнение регрессии потребления материалов 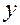от объема производства , построенное по 20 наблюдениям, имеет вид:
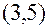
В скобках – фактическое значение t – критерия. Коэффициент детерминации для этого уравнения равен:
+—0,405
—0,428
—0,292
—0,501
Уравнение регрессии потребления материалов 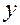от объема производства , построенное по 15 наблюдениям, имеет вид:
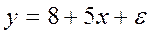
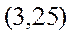
В скобках – фактическое значение t – критерия. Коэффициент детерминации для этого уравнения равен:
+—0,448
—0,564
—0,356
—0,621
Уравнение регрессии потребления материалов от объема производства , построенное по 20 наблюдениям, имеет вид:
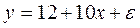
В скобках – фактическое значение t – критерия. Коэффициент детерминации для этого уравнения равен:
+—0,491
—0,425
—0,379
—0,531
Уравнение регрессии потребления материалов от объема производства , построенное по 18 наблюдениям, имеет вид:
В скобках – фактическое значение t – критерия. Коэффициент детерминации для этого уравнения равен:
+—0,327
—0,425
—0,517
—0,369
Уравнение регрессии потребления материалов 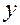от объема производства , построенное по 25 наблюдениям, имеет вид:
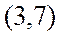
В скобках – фактическое значение t – критерия. Коэффициент детерминации для этого уравнения равен:
+—0,373
—0,321
—0,415
—0,512
Уравнение регрессии потребления материалов 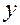от объема производства , построенное по 15 наблюдениям, имеет вид:
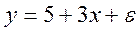
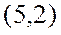
В скобках – фактическое значение t – критерия. Коэффициент детерминации для этого уравнения равен:
+—0,675
—0,519
—0,631
—0,620
Уравнение регрессии потребления материалов 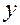от объема производства , построенное по 18 наблюдениям, имеет вид:
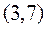
В скобках – фактическое значение t – критерия. Коэффициент детерминации для этого уравнения равен:
+—0,461
—0,395
—0,423
—0,522
Уравнение регрессии потребления материалов 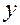от объема производства , построенное по 20 наблюдениям, имеет вид:
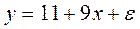
В скобках – фактическое значение t – критерия. Коэффициент детерминации для этого уравнения равен:
+—0,495
—0,517
—0,444
—0,396
По совокупности 15 предприятий торговли изучается зависимость между ценой на товар А и прибылью 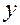торгового предприятия. При оценке регрессионной модели были получены следующие результаты:
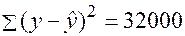
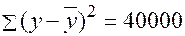
Индекс корреляции, фактическое значение F- критерия значимость уравнения регрессии следующие:
+— 
уравнение статистически не значимо на уровнях 0,01 и 0,05
— 
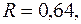
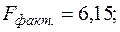уравнение статистически значимо только на уровне 0,1
— 
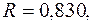
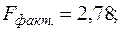уравнение статистически значимо только на уровнях 0,1 и 0,05
— 
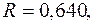
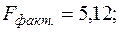уравнение статистически значимо на всех уровнях
По совокупности 18 предприятий торговли изучается зависимость между ценой на товар А и прибылью 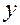торгового предприятия. При оценке регрессионной модели были получены следующие результаты:
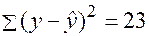
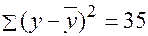
Определить индекс корреляции и фактическое значение F- критерия, а также статистическую значимость уравнения регрессии
+— 
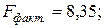уравнение статистически значимо на уровнях 0,05 и 0,1
— 
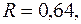
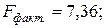уравнение статистически не значимо на уровне 0,01
— 
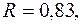
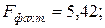уравнение статистически значимо на всех уровнях
— 
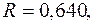
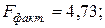уравнение статистически не значимо на всех уровнях
