Нанесення розмірів ГОСТ 2. 307-68

Розміри наносяться за допомогою розмірних чисел, розмірних і виносних ліній.

Розмірна лінія визначає границі вимірювання. Її проводять паралельно відрізку елемента деталі, розмір якого вимірюється. Розміщується розмірна лінія за межами контуру деталі на відстані 6-10 мм. Розмірні лінії обмежуються стрілками, які упираються у виносні лінії. Величини елементів стрілок розмірних ліній обирають в залежності від товщини лінії видимого контуру і викреслюють їх приблизно однаковими на всьому кресленні. Форма стрілки і приблизне співвідношення її елементів показано на рис. 19.

 

Рис. 19

Виносні лінії перпендикулярні до контурної лінії елемента, виходять за межі розмірних на 1-5 мм.

Розмірне число наносять над розмірною лінією і по можливості ближче до середини,між розмірною лінією і розмірним числом повинна бути відстань в 1 мм.

Розмірні числа наносяться креслярським шрифтом 3,5-5 мм та нахилом 75° до розмірної лінії.

Основні вимоги нанесення розмірів:

1. Основою для визначення величини зображеного виробу та його елементів слугують розмірні числа, нанесені на креслення.

2. Загальна кількість розмірів на креслені повинна бути мінімальною, але достатньою для виготовлення та контролю виробу.

3. Розміри, які не підлягають виконанню по даному креслені і вказуються для зручності користування кресленням, називаються довідковими.

4. Довідкові розміри на креслені позначаються знаком «*», а в технічних вимогах записують: «* розміри для довідок». Якщо всі розміри на креслені довідкові, то їх знаком «*» не позначають, а в технічних вимогах записують: «розміри для довідок».

5. До довідкових відносяться наступні розміри:

а). один із розмірів замкненого розмірного ланцюга (рис. 20);

* Розмір для довідок

Рис. 20 Рис. 21

б). розміри на складальному креслені, по яких визначають граничні положення окремих елементів конструкцій, наприклад хід поршня, хід клапана двигуна внутрішнього згорання і т.п.;

в). розміри на складальному креслені, які перенесені з креслень деталей і використовуються в якості встановлюючих та з’єднальних;

г). габаритні розміри на складальному креслені, які перенесені з креслень деталей або являються сумою розмірів декількох деталей;

6. Не допускається повторювати як виконавчі розміри одного і того ж елементу на різних зображеннях, в технічних вимогах і в специфікації (рис. 22).

Рис.22

7. Лінійні розміри на кресленнях і в специфікаціях вказують в міліметрах, без зазначення одиниці вимірювання.

Для розмірів, які вказуються в технічних вимогах і пояснювальних написах на полі креслення, обов’язково вказують одиниці вимірювання.

8. Кутові розміри вказують в градусах, хвилинах та секундах з позначенням одиниці вимірювання, наприклад: 4°; 4°30'; 12°45'30''; 0°30'40''; 0°18'; 0°5'25''; 30°±1°; 30°±10'.

9. Для розмірних чисел застосовувати звичайні дроби не допускається, за виключенням розмірів в дюймах.

10. Розміри, які визначають розміщення поверхонь спряження, проставляють, як правило, від конструктивних баз з врахуванням можливостей виконання і контролю цих розмірів.

11. При розміщені елементів предмету (отворів, пазів, зубів і т.п.) на одній осі або на одній окружності розміри, які визначають їх взаємне розміщення, наносять наступними способами.

а). від загальної бази (поверхні, осі) (рис. 23 а). і б).);

б). заданням розмірів декількох груп елементів від декількох загальних баз (рис. 23 в).);

Рис. 23

в). заданням розмірів між суміжними елементами (ланцюгом) (рис. 24).

Рис. 24

12. Розміри на кресленнях не можна наносити у вигляді замкненого ланцюга, за винятком випадків, коли один з розмірів вказаний як довідковий (рис. 20).

Розміри, які визначають положення симетрично розміщених поверхонь симетричних виробів, наносять, як показано на рис. 25.

Рис. 25

Основні розміри на креслення наносяться:

1. Розміри на кресленнях вказують розмірними числами і розмірними лініями.

2. При нанесені розміру прямолінійного відрізку розмірну лінію проводять паралельно даному відрізку, а виносні лінії – перпендикулярно розмірним (рис. 26).

3. При нанесені розміру кута розмірну лінію проводять у вигляді дуги з центром в його вершині, а виносні лінії – радіально (рис. 27).

4. При нанесені розміру дуги окружності розмірну лінію проводять концентрично дузі, а виносні лінії – паралельно бісектрисі кута, над розмірним числом наносять знак «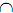» (рис. 28).

5. Розмірну лінію з обох кінців обмежують стрілками, які впираються у відповідні лінії (контурні, виносні, осьові), а при нанесенні розміру радіуса дуги стрілку проставляють з внутрішньої або зовнішньої сторони дуги. (рис. 29).

Рис. 26	Рис. 27	Рис. 28	Рис. 29

6. У випадках, показаних на рис. 30, розмірну та виносну лінію проводять так, щоб вони разом з відрізком, який вимірюється, утворювали паралелограм.

7. Розмірні лінії зазвичай наносять поза контуром зображення.

8. Виносні лінії повинні виходити за межі кінців стрілок розмірної лінії на 1…5 мм.

9. Мінімальна відстань між паралельними розмірними лініями повинна бути 7 мм, а між розмірною і лінією контуру – 10 мм і обрані в залежності від розмірів зображення і насиченості креслення.

10. Не допускається перетин розмірних ліній будь-якими іншими лініями. Виносні лінії можуть перетинатися між собою. (рис. 31).

Рис. 30	Рис. 31

11. Не допускається використання лінії контуру, осьові, центрові і виносні лінії в якості розмірних.

12. Якщо треба показати координати вершини округленого кута або центру дуги округлення, то виносні лінії проводять від точки перетину сторін округленого кута або центра дуги округлення (рис. 30 і 31).

13. Якщо вид або розріз симетричного предмета або окремих симетрично розміщених елементів зображують тільки до осі симетрії або з обривом, то розмірні лінії, які відносяться до цих елементів, проводять з обривом, і обрив розмірної лінії виконують далі від осі або лінії обриву предмета (рис. 32).

Рис. 32

14. Розмірні лінії допускається проводити з обривом в наступних випадках:

а). при зазначені розміру діаметра окружності незалежно від того, зображена і окружність повністю або частково; при цьому обрив розмірної лінії роблять далі від центра окружності (рис. 33);

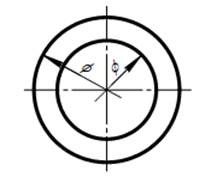
Рис. 33

 

б). при нанесені розмірів від бази, яка не зображена на даному креслені (рис. 34).

Рис. 34	Рис. 35

15. При зображені виробів з розривом розмірну лінію не переривають (рис. 35).

16. Якщо довжина розмірної лінії недостатня для розміщення на ній стрілок, то розмірну лінію продовжують за виносні лінії (або відповідно за контурні, осьові, центрові і т.д.) і стрілки виносять, як показано на рис. 36.

Рис. 36

17. При недостатній кількості місця для стрілок на розмірних лініях, розміщених ланцюгом, стрілки допускається заміняти засіками, які наносять під кутом 45° до розмірних ліній (рис. 37), або чітко нанесеними точками (рис. 38).

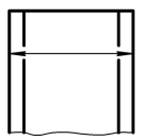
18. При недостатній кількості місця для стрілки із-за близько розміщеної контурної або виносної лінії останні допускається переривати (рис. 39).

Рис. 37	Рис. 38	Рис. 39

19. Розмірні числа наносять над розмірною лінією по можливості ближче до її середини (рис. 40).

Рис. 40

20. При нанесені розміру діаметра всередині окружності розмірні числа зміщують відносно середини розмірних ліній.

21. При нанесенні декількох паралельних або концентричних розмірних ліній на невеликій відстані одна від одної розмірні числа над ними рекомендується розміщувати в шаховому порядку (рис. 41).

Рис. 41

22. Розмірні числа лінійних розмірів при різних нахилах розмірних ліній розміщують як показано на рис. 42.

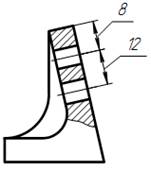
Якщо необхідно нанести розмір в заштрихованій зоні, відповідне розмірне число наносять на поличці-виносці (рис. 43).

Рис. 42	Рис. 43

23. Кутові розміри наносять так, як показано на рис. 44.

Для кутів малих розмірів при недостатній кількості місця розмірні числа поміщають на поличках-виносках в будь-якій зоні (рис. 45).

 

Рис. 44	Рис. 45

24. Якщо для написання розмірного числа недостатньо місця над розмірною лінією, то розміри наносять як показано на рис. 46; якщо недостатньо місця для нанесення стрілок, то їх наносять як показано на рис. 47.

Спосіб нанесення розмірного числа при різноманітних положеннях ліній (стрілок) на кресленні визначається найбільшою зручністю читання.

Рис. 46	Рис. 47

25. Розмірні числа не допускається розділяти або перетинати будь-якими лініями креслення. Не допускається розривати лінію контуру для нанесення розмірного числа в місцях перетинання розмірних, осьових або центрових ліній. В місці нанесення розмірного числа осьові, центрові лінії і лінії штриховки переривають (рис. 48 і 49).

26. Розміри, які відносяться до одного і того ж конструктивного елементу (пазу, виступу, отвору і т.п.), рекомендується групувати в одному місці, розміщуючи їх на тому зображенні, на якому геометрична форма даного елементу показана найбільш повно (рис. 50).

Рис. 48	Рис. 49	Рис. 50

27. При нанесені розміру радіуса перед розмірним числом розміщують прописну літеру R.

28. Якщо при нанесені розміру радіуса дуги окружності необхідно вказати розмір, який визначає положення її центра, то останній зображують у вигляді перетину центрових або виносних ліній.

При великій величині радіуса центр дозволяється наближувати до дуги, в даному випадку розмірну лінію радіуса показують зі зломом під кутом 90° (рис. 51).

29. Якщо не потрібно вказувати розміри, які визначають положення центра дуги окружності, то розмірну лінію радіуса допускається не доводити до центра і зміщувати її відносно центра (рис. 52).

 

Рис. 51	Рис. 52

30. При побудові декількох радіусів із одного центра розмірні лінії будь-яких двох радіусів не розміщуються на одній прямій (рис. 53).

При співпаданні центрів декількох радіусів їх розмірні лінії допускається не доводити до центра, окрім крайніх (рис. 54).

 

Рис. 53	Рис. 54

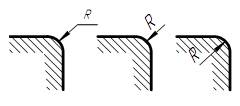
31. Розміри радіусів зовнішніх округлень наносять як показано на рис. 55, внутрішніх округлень – на рис. 56.

Рис. 55	Рис. 56

Розміри однакових радіусів допускається вказувати на спільній поличці, як показано на рис. 57.

Рис. 57

32. При вказуванні розміру діаметра (у всіх випадках) перед розмірним числом наносять знак «».

33. Перед розмірним числом діаметра (радіуса) сфери також наносять знак (R) без напису «Сфера». Якщо на кресленні важко відрізнити сферу від інших поверхонь, то перед розмірним числом діаметра (радіуса) допускається наносити слово «Сфера» або знак «Ο», наприклад: «Сфера 18, Ο R 12».

34. Розмір квадрата наносять як показано на рис. 58, 59 і 60.

Рис. 58	Рис. 59	Рис. 60

Висота знака 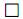повинна бути рівна висоті розмірних чисел на кресленні.

35. Перед розмірним числом, що характеризує конусність, наносять знак «», гострий кут якого повинен бути направлений в сторону вершини конуса (рис. 61).

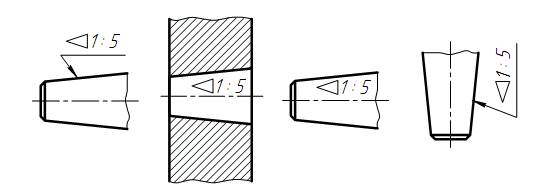
Рис. 61

 

Знак конуса і конусність у вигляді співвідношення слід наносити над осьовою лінією або на поличці-виносці.

36. Кут поверхні слід вказувати безпосередньо біля зображення поверхні нахилу або на поличці-виносці у вигляді співвідношення (рис. 62а), у відсотках (рис. 62б). перед розмірним числом, яке визначає нахил, наносять знак «», гострий кут якого повинен бути направлений в сторону нахилу.

Рис. 62

37. Розміри фасок під кутом 45° наносять як показано на рис. 63.

Рис. 63

 

Розміри фасок під іншими кутами вказують керуючись загальними правилами – лінійним та кутовим розмірами (рис. 64а, б) або двома лінійними розмірами (рис. 64в).

Рис. 64

38. Розміри декількох однакових елементів виробу, як правило, наносять один раз з вказівкою їхньої кількості на поличці лінії-виноски (рис. 65а).

Допускається вказувати кількість елементів (рис. 65б).

39. При нанесенні розмірів елементів, рівномірно розміщених по окружності виробу (наприклад, отворів), замість кутових розмірів, визначаючих взаємне розміщення елементів, вказують тільки їх кількість (рис. 66-68).

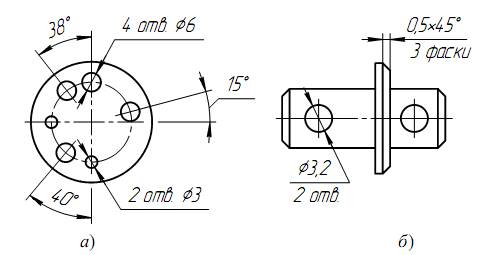
Рис. 65

Рис. 66	Рис. 67	Рис. 68

40. Розміри двох симетрично розміщених елементів виробу (окрім отворів) наносять один раз без вказування їх кількості, групуючи, як правило, в одному місці всі розміри (рис. 69 і 70).

Рис. 69	Рис. 70

Повністю вказують кількість однакових отворів, а їх розміри – тільки один раз.

41. При нанесенні розмірів, визначаючих відстань між рівномірно розміщеними однаковими елементами виробу (наприклад, отворами), рекомендується замість розмірних ланцюгів наносити розміри між сусідніми елементами і розмір між крайніми елементами у вигляді добутку кількості проміжків між елементами на розмір проміжку (рис. 71).

Рис. 71

 

ЛЕКАЛЬНІ КРИВІ

Дуже часто в техніці зустрічаються плоскі криві: еліпс, парабола, гіпербола, циклоїда, синусоїда, евольвента та інші. Вони обводяться за допомогою лекала.

4.1. Еліпс – плоска замкнена крива, яка представляє собою геометричні місця точок, сума відстаней від яких до двох заданих точок, які називаються фокусами, являється постійною величиною.

Методи побудова еліпса:

- Побудова еліпса за його фокусами;

- Побудова еліпса по координатним точкам;

- Побудова еліпса по двох осях;

- Побудова еліпса по спряженим діаметрам.

Побудова еліпса одним з методів приведено на рис. 72.

Дано: АВ – велика вісь еліпса;

СД – мала ось еліпса.

Для побудови еліпса по великій і малій осях через точку О – центр еліпса – проводять дві взаємно перпендикулярні прямі у напряму осей еліпса. Із центра О проводять дві допоміжні концентричні окружності з діаметрами, які рівні великій і малим осям еліпса. Точки А, Б, С і Д, побудовані на перпендикулярних прямих, належать еліпсу як кінці його осей.

Для знаходження проміжних точок окружність ділять на декілька рівних частин, наприклад 12; точки поділу повинні лежати на великій окружності. Відмічають, наприклад, точки М і N. Провівши через точку М пряму, паралельну малій осі еліпса (СД), а через точку N – пряму, паралельну великій осі еліпса (АВ), отримують на їх перетині точку Е, яка належить еліпсу. Аналогічно можна знайти будь яке число точок еліпса. З’єднуючи за допомогою лекала знайдені точки. Будують еліпс.

Для побудови дотичної і нормалі в точці К, треба з’єднати точку К з фокусами і розділити навпіл кут між радіус-векторами і ; бісектриса внутрішнього кута і є нормаллю, а перпендикулярна до неї бісектриса зовнішнього кута – дотична.

Рис. 72

4.2. Параболою називається крива, яка є геометричним місцем точок площини, рівновіддалених від даної точки (що називається фокусом), і даної прямої тієї ж площини (директриси параболи).

Методи побудови параболи:

- За заданими директрисою і фокусом;

- За заданими вершиною, віссю і одною із точок параболи (рис. 73);

- За допомогою дотичних прямих до параболи.

Розглянемо спосіб побудови параболи за направленням вісі, вершини і однієї з точок на її очерті. Сторони А6 і 66 ділимо на однакове число рівних частин. Перетин променя А5 з прямою, паралельною осі АВ і проведеної через точку 5, яка знаходиться на прямій А5, визначає точку 5', яка належить очерті параболи. Аналогічно знаходять положення точок 4', 3' та інш.

Дотична до параболи в даній точці М є бісектрисою кута ГMN. Якщо фокус невідомий – опускають з точки М на вісь перпендикуляр і відкладають від вершини відрізок АВ=ОА. Дотична проходить через точки О і М. нормаль перпендикулярна до дотичної.

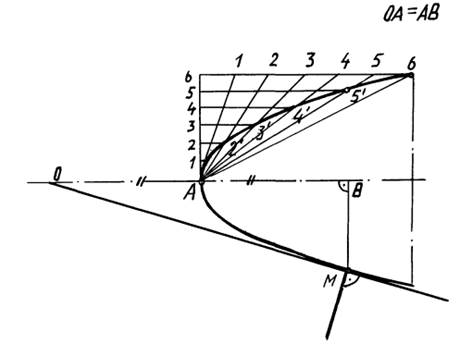
Рис. 73

4.3. Гіперболою називається геометричне місце точок площини, різниця відстаней від яких до двох заданих точок – фокусів – є величина постійна, рівна відстані між вершинами гіперболи.

Існує декілька способів побудови гіперболи. Розглянемо один з них (рис. 74). Для побудови задається одна з точок гіперболи, наприклад, точка М. Через точку М проводять прямі та паралельні асимптотам та . Із точки О перетину осей проводять прямі, які перетинають прямі та . Дал і зточок перетину з цими прямими проводять прямі паралельні асимптотам до їх взаємного перетину в точці 1. Аналогічно можна знайти будь-яке число точок гіперболи. Отримані точки гіперболи з’єднують за допомогою лекала.

Дотична до гіперболи в точці n проводиться як бісектриса кута .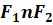

Рис. 74

4.4. Синусоїдою називається траєкторія точки, яка рухається по циліндричній гвинтовій лінії, на площину, паралельну осі циліндра. Рух точки складається із рівномірно-обертового руху (навколо осі циліндра) і рівномірно-поступального (паралельно осі циліндра). Синусоїда – це плоска крива, яка показує зміну тригонометричної функції синуса в залежності від зміни величини кута.

Для побудови синусоїди окружність ділять на довільне число рівних частин, наприклад 12. На це ж число частин ділять і пряму АВ, довжина якої дорівнює довжині хвилі. Із отриманих та пронумерованих точок проводять взаємно перпендикулярні прямі. Отримані точки перетину цих прямих з’єднують за допомогою лекала плавною кривою (рис. 75).

 

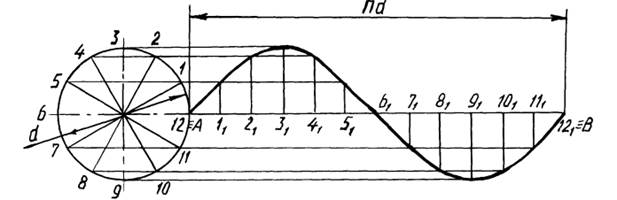
Рис. 75

4.5. Евольвента окружності. Евольвентою або розгорткою окружності називається плоска крива, яка є траєкторією точки окружності, утвореною її розгортанням і витравлюванням (рис. 76). Для побудови евольвенти окружності радіуса R ділять на декілька рівних частин, наприклад 12. В точках поділу 1, 2, 3, …, 12 проводять дотичні до окружності. На дотичній в точці 12 відкладають довжину окружності (2πR), яку ділять на ту ж кількість рівних частин. Послідовно на дотичних відкладають 1/12, 2/12, …, 12/12 довжини окружності. Отримані точки з’єднують за допомогою лекала плавною кривою. Дотична до евольвенти, наприклад в точці Х, перпендикулярна до дотичної Х-10 окружності.

Рис. 76

4.6. Спіралью Архімеда називаєтья плоска крива, яка описується точкою, що рівномірно рухається по радіус-вектору, який в той же час рівномірно обертається в площині навколо неподвижної точки О. Розглянемо побудову спіралі Архімеда по заданим центру і кроку (рис. 77).

Проведемо окружність, відрізок О 12 і окружність ділять на рівне число частин, наприклад на дванадцять; через точки ділення окружності 1, 2, …, 12 і центр О проводять промені, на яких від центру О відкладають відрізки відповідно рівні 1/12, 2/12 і т.д. кроку спіралі. Лекальна крива, яка з’єднує отримані на променях точки, і буде шуканою спіраллю.

Рис. 77

4.7. Циклоїда є плоскою кривою, що представляє собою траєкторію точки А утворюючої окружності, яка котиться без ковзання по нерухомій прямій (рис. 78).

Для побудови циклоїди проводять окружність даного радіуса і ділять її на довільне число рівних частин (наприклад 12). На заданій направляючій горизонтальній прямій А відкладають довжину окружності, рівної 2πR і ділять її на таке ж число рівних частин. Із точок ділення прямої 1, 2, …, 12 встановлюють перпендикуляри до перетину їх з прямою, яка проходить через центр О паралельно А , в точках . З цих точок, як з центрів, роблять засіки на відповідних лініях, проведених паралельно горизонтальній осі, через точки ділення окружності, що котиться. У результаті отримують точки, які належать циклоїді. Пряма N8, яка з’єднує точку N з точкою 8 дотику окружності, яка котиться, до направляючої А , є нормаллю циклоїди в даній точці; перпендикуляр опущений до N8 – дотична.

Рис. 78

Побудова епіциклоїди і гіпоциклоїди. Епіциклоїду і гіпоциклоїду можна розглядати як окремі випадки циклоїди, коли направляюча пряма А перетворюється в дугу окружності. При перекочуванні утворюючої окружності радіуса r із зовнішньої сторони направляючої окружності радіуса R отримується епіциклоїда (рис. 79), при перекочуванні утворюючої окружності всередині направляючої – гіпоциклоїда. Довжина дуги А визначається центральним кутом α=360° .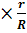

Побудова точок епіциклоїди та гіпоциклоїди проводиться також, як для циклоїди, з тією різницею, що всі прямі, які паралельні лінії А , замінюються концентричними дугами, а перпендикуляри до лінії А - радіусами. Епіциклоїда, яку отримують при R=r, називається кардіоїдой. Гіпоциклоїда, яку отримують при R=4r, називається астроідой. При R=2r гіпоциклоїда перетворюється в пряму, яка являється діаметром направлюючої окружності.

 

Рис. 79