Розглянемо дві прямі m, n, що перетинаються і радіус спряження R (рис. 12). Необхідно побудувати спряження даних прямих окружністю радіусом R.
Рис. 12
Виконуємо наступні побудови:
1. Побудуємо множину точок центрів спряження, віддалених від прямої n на відстань радіуса R спряження. Такою множиною являється пряма n¹, паралельна даній прямій n і віддалена від неї на відстань R.
2. Побудуємо множину точок центрів спряження, віддалених від прямої m на відстань радіуса спряження. Такою множиною являється пряма m¹, паралельна m і віддалена від останньої на відстань R.
3. На перетині побудованих прямих m¹ і n¹ знаходимо центр спряження О.
4. Визначимо точку А спряження прямої n. Для цього опустимо із центру О перпендикуляр на пряму n. Для визначення точки спряження В на прямій m, необхідно опустити відповідно перпендикуляр із центра О на пряму m. Проведемо дугу спряження АВ. Тепер будуть визначені всі елементи спряження: радіус, центр і точки спряження.
Спряження прямої з окружністю
Спряження прямої з окружністю може бути зовнішнім та внутрішнім. Розглянемо побудову зовнішнього спряження прямої з окружністю.
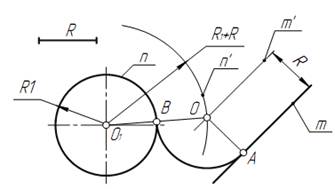
Приклад 1. Нехай задано окружність радіусом R з центром в точці 
і пряма m. Необхідно побудувати спряження окружності з прямою дугою окружності заданого радіуса R (рис. 13).
Для рішення задачі виконаємо наступні побудови:
1. Побудуємо множину точок центрів спряження, які віддалені від прямої спряження на відстань R. Цю множину задає пряма m¹, паралельна m і віддалена від неї на відстань R.
2. Множина точок центрів спряження, віддалених від окружності n на відстань R, являється окружність n¹, яка проведена радіусом R1+R.
3. Центр спряження О знаходимо як точку перетину лінії n¹ і m¹.
4. Точка спряження А знаходиться як основа перпендикуляра, проведеного із точки О на пряму m. Щоб побудувати точку спряження В, необхідно провести лінію центрів О , тобто з’єднати центри спряження дуг. На перетині лінії центрів з заданою окружністю визначимо точку В.
5. Побудуємо дугу спряження АВ.
| 
|
| Рис. 13 | Рис. 14 |
Приклад 2. При побудові внутрішнього спряження (рис. 14) послідовність побудови залишається такою ж, як і в прикладі 1. Але центр спряження визначається за допомогою допоміжної дуги окружності, яка проведена із центра , радіусом R-R1.
Спряження окружностей
Спряження двох окружностей може бути зовнішнім, внутрішнім і змішаним. Нехай задано радіус спряження R, а центри спряження і точки спряження треба знайти.
Приклад 1. Побудуємо спряження з зовнішнім дотиком двох даних окружностей m i n з радіусами R1 і R2 дугою заданого радіуса R (рис. 15а).
1. Для знаходження центра спряження О проведемо окружність m¹, віддалену від даної окружності m на відстань R. Так як спряження з зовнішнім торканням, то радіус окружності m¹ рівний R1+R.
2. Радіусом R2+R проведемо окружність n¹, яка віддалена від даної окружності n на відстань R.
3. Знайдемо центр спряження О як точку перетину окружностей m¹ і n¹.
4. Знайдемо точку спряження А, як перетин ліній центрів О з дугою m.
5. Аналогічно знайдемо точку В, як перетин ліній центрів О 
з дугою n.
6. Проведемо дугу спряження АВ.
Рис. 15
Приклад 2. Побудуємо спряження з внутрішнім торканням двох даних окружностей m і n з радіусами R1 і R2 дугою радіусом R (рис. 15б).
1. Для знаходження центра спряження О проведемо окружність m¹ на відстані R-R1 від даної окружності m.
2. Проведемо окружність n¹ на відстані R-R2 від даної окружності n.
3. Центр спряження О знайдемо як точку перетину окружностей m¹ і n¹.
4. Точку спряження А знайдемо як точку перетину ліній центрів О з заданою окружністю m.
5. Точку спряження В знайдемо як точку перетину ліній центрів О з заданою окружністю n.
6. Проведемо дугу спряження АВ з центром в точці О.
Приклад 3. На рис. 16 представлено приклад побудови спряження з змішаним торканням.
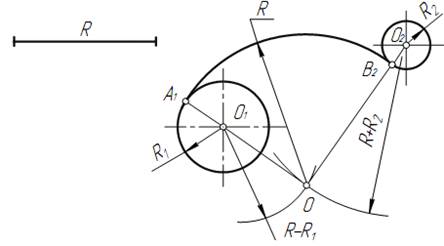
Рис. 16
Побудова дотичних
Приклад 1. Дано окружність з центром в точці і точка за нею. Через дану точку провести дотичну до даної окружності (рис. 17).
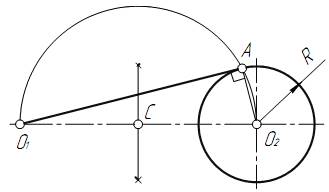
Рис. 17
Для рішення задачі виконаємо наступні побудови:
1. З’єднаємо точку з центром окружності .
2. Знайдемо середину С відрізка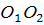 
.
3. Із точки С, як з центра, проведемо допоміжну окружність радіусом С =С .
4. В точці перетину допоміжної окружності з заданою отримаємо точку торкання А. З’єднаємо точку з точкою А.
Приклад 2. Побудуємо спільну дотичну АВ до двох заданих окружностей радіусами R1 і R2 (рис. 18).
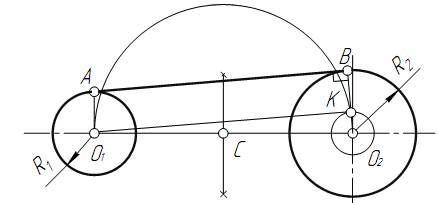
Рис. 18
1. Знаходимо середину С відрізка .
2. Із точки С, як із центра, радіусом С =С проведемо допоміжну окружність.
3. Із центру великої окружності проведемо другу допоміжну окружність радіусом R2-R1.
4. Перетин двох допоміжних окружностей визначає точку К, через яку проходить радіус К, що проходить до точки дотику В.
5. Для побудови другої точки дотику А проведемо А|| В.
6. З’єднаємо точки А і В відрізком прямої лінії.
